本文最后更新于：2024年5月7日 下午

图像中存在很多物体拐角，本文记录像素级角点检测算法 Harris 和 Shi Tomasi。

角点简介

在现实世界中，角点对应于物体的拐角，道路的十字路口、丁字路口等。从图像分析的角度来定义角点可以有以下两种定义：

  1. 角点可以是两个边缘的角点；
  2. 角点是邻域内具有两个主方向的特征点；

一提到角点检测，最常用的方法莫过于Harris角点检测，opencv 中也提供了 Harris 角点检测的接口，即cornerHarris()，但是 Harris 角点检测存在很多缺陷（如角点是像素级别的，速度较慢等），opencv 中有另一个功能更为强大的函数— goodFeaturesToTrack()，它不仅支持 Harris 角点检测，也支持 Shi Tomasi 算法的角点检测。但是，该函数检测到的角点依然是像素级别的。

角点检测基本原理

人眼对角点的识别通常是在一个局部的小区域或小窗口完成的。如果在各个方向上移动这个特征的小窗口，窗口内区域的灰度发生了较大的变化，那么就认为在窗口内遇到了角点。如果这个特定的窗口在图像各个方向上移动时，窗口内图像的灰度没有发生变化，那么窗口内就不存在角点；如果窗口在某一个方向移动时，窗口内图像的灰度发生了较大的变化，而在另一些方向上没有发生变化，那么，窗口内的图像可能就是一条直线的线段。

对于图像 $I(x,y)$,当在点 $(x,y)$ 处平移 $(\Delta x,\Delta y)$ 后的自相似性，可以通过自相关函数给出:
$$
c(x, y ; \Delta x, \Delta y)=\sum_{(u, v) \in W(x, y)} w(u, v)(I(u, v)-I(u+\Delta x, v+\Delta y))^{2}
$$
其中， $ W(x, y) $ 是以点 $ (x, y) $ 为中心的窗口， $ w(u, v) $为加权函数，它既可是常数，也可以是高斯加权函数。

根据泰勒展开，对图像 $ I(x, y) $ 在平移 $ (\Delta x, \Delta y) $ 后进行一阶近似：
$$
I(u+\Delta x, v+\Delta y)=I(u, v)+I_{x}(u, v) \Delta x+I_{y}(u, v) \Delta y+O\left(\Delta x^{2}, \Delta y^{2}\right) \approx I(u, v)+I_{x}(u, v) \Delta x+I_{y}(u, v) \Delta y
$$
其中， $ I_{x}, I_{y} $ 是图像 $ I(x, y) $ 的偏导数，这样的话，自相关函数则可以简化为：
$$
c(x, y ; \Delta x, \Delta y) \approx \sum_{w}\left(I_{x}(u, v) \Delta x+I_{y}(u, v) \Delta y\right)^{2}=[\Delta x, \Delta y] M(x, y)\left[\begin{array}{l}\Delta x \ \Delta y\end{array}\right]
$$
其中：
$$
\begin{array}{c}M(x, y)&=&\sum_{w}\left[\begin{array}{cc}I_{x}(x, y)^{2} & I_{x}(x, y) I_{y}(x, y) \ I_{x}(x, y) I_{y}(x, y) & I_{y}(x, y)^{2}\end{array}\right]\&=&\left[\begin{array}{cc}\sum_{w} I_{x}(x, y)^{2} & \sum_{w} I_{x}(x, y) I_{y}(x, y) \ \sum_{w} I_{x}(x, y) I_{y}(x, y) & \sum_{w} I_{y}(x, y)^{2}\end{array}\right] \ &=&\left[\begin{array}{ll}A & C \ C & B\end{array}\right]\end{array}
$$
也就是说图像 $ I(x, y) $ 在点 $ (x, y) $ 处平移 $ (\Delta x, \Delta y) $ 后的自相关函数可以近似为二项函数：
$$
c(x, y ; \Delta x, \Delta y) \approx A \Delta x^{2}+2 C \Delta x \Delta y+B \Delta y^{2}
$$
其中：
$$
A=\sum_{w} I_{x}^{2}, B=\sum_{w} I_{y}^{2}, C=\sum_{w} I_{x} I_{y}
$$
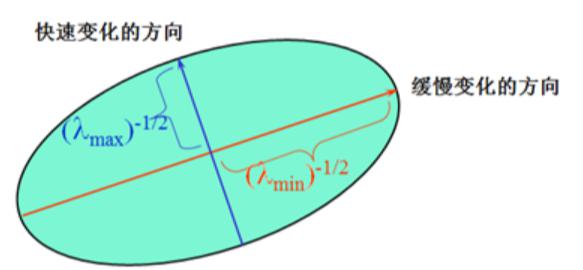
二次项函数本质上就是一个椭圆函数。椭圆的扁率和尺寸是由 $ M(x, y) $ 的特征值 $ \lambda_{1} 、 \lambda_{2} $ 决定的，椭圆的方向是由 $ M(x, y) $ 的特征矢量决定的，如下图所示，椭圆方程为：
$$
[\Delta x, \Delta y] M(x, y)\left[\begin{array}{l}\Delta x \ \Delta y\end{array}\right]=1
$$

Harris角点算法实现

根据上述讨论，可以将 Harris 图像角点检测算法归纳如下，共分以下五步：

  1. 计算图像 $I(x,y)$ 在 $X$ 和 $Y$ 两个方向的梯度$I_x、I_y$。
    $$
    I_{x}=\frac{\partial I}{\partial x}=I \otimes(-101), I_{y}=\frac{\partial I}{\partial x}=I \otimes(-101)^{T}
    $$

  2. 计算图象两个方向梯度的乘积。
    $$
    I_{x}^{2}=I_{x} \cdot I_{y}, I_{y}^{2}=I_{y} \cdot I_{y}, I_{x y}=I_{x} \cdot I_{y}
    $$

  3. 使用高斯函数对 $ I_{x}^{2} 、 I_{y}^{2} $ 和 $ I_{x y} $ 进行高斯加权 ( 取 $ \sigma=1 $ )，生成矩阵 $ M $ 的元素 $ A 、 B $ 和 $ C $ 。

    $$ A=g\left(I_{x}^{2}\right)=I_{x}^{2} \otimes w, C=g\left(I_{y}^{2}\right)=I_{y}^{2} \otimes w, B=g\left(I_{x, y}\right)=I_{x y} \otimes w $$

  4. 计算每个像素的 Harris 响应值 $R$ ,并对小于某一阈值的 $R$ 置为零。

    $$ R=\left\{R: \operatorname{det} \boldsymbol{M}-\alpha(\text { trace } \boldsymbol{M})^{2}

  5. 在 $ 3 \times 3 $ 或 $ 5 \times 5 $ 的邻域内进行非最大值抑制，局部最大值点即为图像中的角点。

    其中：
    $$
    M(x, y)=\sum_{w}\left[\begin{array}{cc}I_{x}(x, y)^{2} & I_{x}(x, y) I_{y}(x, y) \ I_{x}(x, y) I_{y}(x, y) & I_{y}(x, y)^{2}\end{array}\right]=\left[\begin{array}{cc}\sum_{w} I_{x}(x, y)^{2} & \sum_{w} I_{x}(x, y) I_{y}(x, y) \ \sum_{w} I_{x}(x, y) I_{y}(x, y) & \sum_{w} I_{y}(x, y)^{2}\end{array}\right]=\left[\begin{array}{cc}A & C \ C & B\end{array}\right]
    $$

$M$ 矩阵特征值

$M(x,y)$ 的特征值由$ \lambda_{1}, \lambda_{2} \leq $组成，特征值$ \lambda_{1}, \lambda_{2} \leq $与图像中的角点、直线（边缘）和平面之间的关系如下图所示:

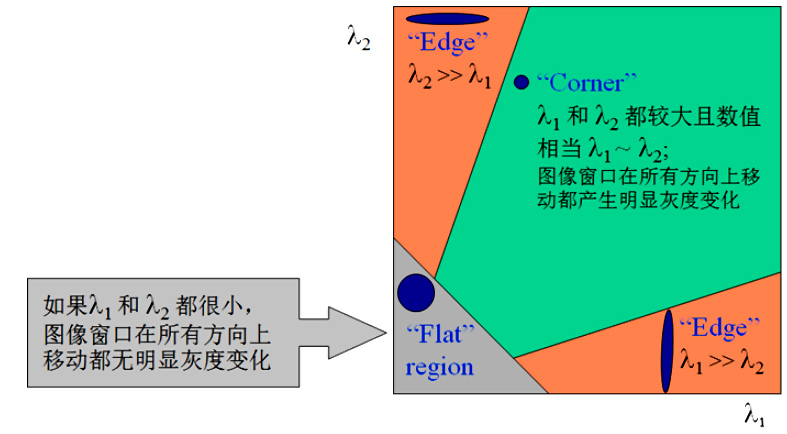
分为三种情况:

  1. 图像中的直线。一个特征值大，另一个特征值小，$λ1≫λ2$ 或 $λ2≫λ1$。自相关函数值在某一方向上大，在其他方向上小。
  2. 图像中的平面。两个特征值都小，且近似相等；自相关函数数值在各个方向上都小。
  3. 图像中的角点。两个特征值都大，且近似相等，自相关函数在所有方向都增大。

Harris 角点判定

根据二次项函数特征值的计算公式，我们可以求 $ M(x, y) $ 矩阵的特征值。但是 Harris 给出的角点差别方法并不需要计 算具体的特征值，而是计算一个角点响应值 $ R $ 来判断角点。 $ R $ 的计算公式为 :
$$
R=\operatorname{det} \boldsymbol{M}-\alpha(\operatorname{trace} M)^{2}
$$
式中， $ \operatorname{det} \boldsymbol{M} $ 为矩阵 $ \boldsymbol{M}=\left[\begin{array}{ll}A & B \ B & C\end{array}\right] $ 的行列式，$trace$ $ M $ 为矩阵 $ M $ 的迹，$α$ 为常数，取值范围为 $0.04~0.06$。事实上，特征隐含在 $\det M$和 $\operatorname{trace} M$中，因为:
$$
\begin{array}{c}
\operatorname{det} \boldsymbol{M}=\lambda_{1} \lambda_{2}=A C-B^{2} \
\operatorname{trace} M=\lambda_{1}+\lambda_{2}=A+C
\end{array}
$$

影响结果的因素

  1. 增大阈值，检测到的角点会减少；

  2. 增大 $α$ 的值，将减小角点响应值 $R$，降低角点检测的灵性，减少被检测角点的数量；

  3. 减小 $α$ 值，将增大角点响应值 $R$，增加角点检测的灵敏性，增加被检测角点的数量；

  4. 同时邻域的大小也会影响角点的检测。

Shi Tomasi 算法

Shi Tomasi 算法，与 Harris 角点检测的区别主要是阈值标准不一样。

Harris 角点采用 $det(M)-α \operatorname{trace}(M)^2$;

Shi Tomasi 算法采用 $min(λ_2,λ_1)$,与阈值进行比较。

OpenCV 对应算子

cornerHarris 函数用于在 OpenCV 中运行 Harris 角点检测算子处理图像。和 cornerMinEigenVal( ) 以及 cornerEigenValsAndVecs( ) 函数类似，cornerHarris 函数对于每一个像素 (x,y) 在 $blockSize*blockSize$ 邻域内，计算 $2 \times 2$ 梯度的协方差矩阵 $M(x,y) $，接着它计算如下式子：
$$
\operatorname{dst}(x, y)=\operatorname{det} M^{(x, y)}-k \cdot\left(\operatorname{tr} M^{(x, y)}\right)^{2}
$$

cornerHarris

函数定义：

1
2
3
void cornerHarris( InputArray src, OutputArray dst, int blockSize,
                                int ksize, double k,
                                int borderType=BORDER_DEFAULT );

参数说明：

参数名 描述
src 输入的单通道 8-bit 或浮点图像。
dst 存储着 Harris 角点响应的图像矩阵，大小与输入图像大小相同，是一个浮点型矩阵。
blockSize 邻域大小。
apertureSize 扩展的微分算子大。
k 响应公式中的，参数$α$。
boderType 边界处理的类型。

goodFeaturesToTrack

函数定义：

1
2
3
4
5
6
7
8
9
10
11
void cv::goodFeaturesToTrack(
		cv::InputArray image, // 输入图像（CV_8UC1 CV_32FC1）
		cv::OutputArray corners, // 输出角点vector
		int maxCorners, // 最大角点数目
		double qualityLevel, // 质量水平系数（小于1.0的正数，一般在0.01-0.1之间）
		double minDistance, // 最小距离，小于此距离的点忽略
		cv::InputArray mask = noArray(), // mask=0的点忽略
		int blockSize = 3, // 使用的邻域数
		bool useHarrisDetector = false, // false ='Shi Tomasi metric'
		double k = 0.04 // Harris角点检测时使用
	);

参数说明：

参数名 描述
image 输入图像（8位或32位单通道图）。
corners 检测到的所有角点，类型为vector或数组，由实际给定的参数类型而定。如果是vector，那么它应该是一个包含cv::Point2f的vector对象；如果类型是cv::Mat,那么它的每一行对应一个角点，点的x、y位置分别是两列。
maxCorners 用于限定检测到的点数的最大值。
qualityLevel 表示检测到的角点的质量水平（通常是0.10到0.01之间的数值，不能大于1.0）。
minDistance 用于区分相邻两个角点的最小距离（小于这个距离得点将进行合并）。
mask 如果指定，它的维度必须和输入图像一致，且在 mask 值为 0 处不进行角点检测。
blockSize 表示在计算角点时参与运算的区域大小，常用值为3，但是如果图像的分辨率较高则可以考虑使用较大一点的值。
useHarrisDetector 用于指定角点检测的方法，如果是 true 则使用 Harris 角点检测，false 则使用Shi Tomasi 算法。
k 在使用Harris算法时使用，最好使用默认值0.04。

Python 实现

测试图像：

示例代码：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
import cv2

img = cv2.imread('sketch.jpg', 0)
orb = cv2.ORB_create()
# detection
pts = cv2.goodFeaturesToTrack(img, 300, qualityLevel=0.22, minDistance=20, useHarrisDetector=False)

# extraction
kps = [cv2.KeyPoint(x=f[0][0], y=f[0][1], size=20) for f in pts]
kps, des = orb.compute(img, kps)

img_with_kp = cv2.drawKeypoints(img, kps, None, color=(0, 255, 0), flags=0)
cv2.imshow('ORB keypoints', img_with_kp)
cv2.waitKey()
pass

结果展示：

参考资料



文章链接：
https://www.zywvvd.com/notes/study/image-processing/corner-det/corner-pix/

“觉得不错的话，给点打赏吧 ୧(๑•̀⌄•́๑)૭”

微信二维码

微信支付

支付宝二维码

支付宝支付

Image_Processing
#Image_Processing
Harris 像素级角点检测
https://www.zywvvd.com/notes/study/image-processing/corner-det/corner-pix/
作者
Yiwei Zhang
发布于
2023年4月10日
许可协议