墨卡托投影法

麦卡托投影法（英语：Mercator projection），又称麦卡托投影法、正轴等角圆柱投影，是一种等角的圆柱形地图投影法。本文记录相关内容。

简介

麦卡托投影法（Mercator projection）又称正轴等角圆柱投影，由荷兰地图学家墨卡托(G.Mercator)于1569年创拟。就是将三维的地球表示在一个二维平面上的方法之一，也是应用得最广泛的方法。

我们平时看到的谷歌地图，百度地图，包括我们的GeoHey地图，都是使用的墨卡托投影。

它以整个世界范围，赤道作为标准纬线，本初子午线作为中央经线，两者交点为坐标原点，向东向北为正，向西向南为负。

麦卡托投影法假设地球被套在一个圆柱中，赤道与圆柱相切，然后在地球中心放一盏灯，把球面上的图形投影到圆柱体上，再把圆柱体展开，就形成以一幅墨卡托投影的世界地图（如下图）。因其等角特性，广泛应用与航空、航海中。

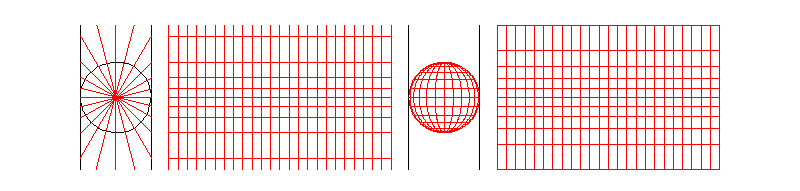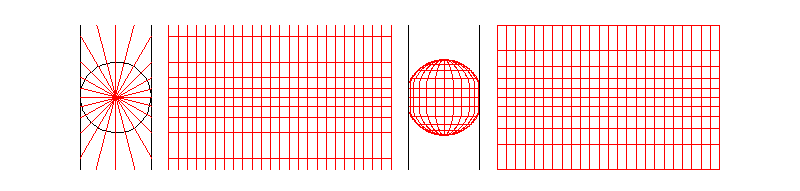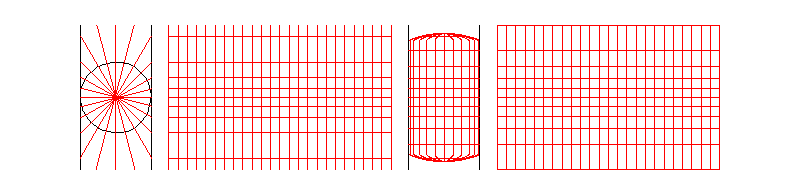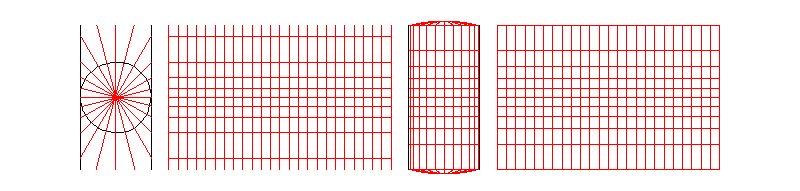
墨卡托投影，是正轴等角圆柱投影，圆柱投影的一种，为地图投影方法中影响最大的投影。假设地球被围在一中空的圆柱里，其基准纬线（赤道）与圆柱相切，然后再假想地球中心有一盏灯，把球面上的图形投影到圆柱面上，再把圆柱面展开，这就是一幅选定基准纬线上的“墨卡托投影”绘制出的地图。其中，按等角条件将经纬网投影到圆柱面上，将圆柱面展为平面后，得平面经纬线网。

从墨卡托投影图上可以看出，经线间隔的经度如果相等，则经线是等距平行的直线，纬线也是平行的直线，而且经纬线是相互垂直的。

墨卡托投影有一个特别的特性：所有罗盘等角线，或称斜航线（就是与所经过的所有经线形成相同角度的航线，也称恒向航线）在墨卡托投影下都是直线。这使得在航海领域这个投影非常重要。

墨卡托投影对透视圆筒投影改造点：要使圆筒投影称为等角的性质，必须使由赤道向两极经线逐渐伸长的倍数与经线上各点相应的纬度扩大的倍数相同。

该方法得名于法兰德斯(佛兰德)出身的地理学家杰拉杜斯·麦卡托，他于1569年发表长202公分、宽124公分以此方式绘制的世界地图。在以此投影法绘制的地图上，将地球在平面展开，经纬线于任何位置皆垂直相交，使世界地图可以绘制在一个长方形，地图的任一点在各种方向的长度均相等。由于可显示任两点间的正确方位，指出真实的经纬度，航海用途的海图、航路图大都以此方式绘制。在该投影中线型比例尺在图中任意一点周围都保持不变，从而可以保持大陆轮廓投影后的角度和形状不变（即等角）；但麦卡托投影会使面积产生变形，赤道地区变化最小，南北两极的变形最大，但因为在南北回归线之间影响很少，而这是多数航线所在区域，所以被广泛用来编制地图。

由于可显示任两点间的正确方位，航海用途的海图、航路图大都以此方式绘制。在该投影中线型比例尺在图中任意一点周围都保持不变，从而可以保持大陆轮廓投影后的角度和形状不变（即等角）；但墨卡托投影会使面积产生变形，极点的比例甚至达到了无穷大。

等角投影

等角投影（Azimuthal Equidistant Projection）是一种地图投影方法，它保持了从投影中心到任何其他点的角度不变。这意味着，在等角投影中，所有从中心点出发到地图上任意点的方向都是准确的，因此它非常适合于导航和定位。

以下是等角投影的一些关键特点：

1. 角度保持：从投影中心到地图上任意点的方向角（方位角）是保持不变的。这意味着，如果你从中心点测量到另一个点的角度，并沿着这个角度移动，你会在实际地球上沿着相同的方向移动。
2. 距离失真：虽然角度保持不变，但距离在等角投影中并不是保持不变的。从投影中心向外，距离会逐渐增大，因此这种投影不适合表示面积或距离。
3. 单一中心点：每个等角投影都有一个中心点，从这个点出发的角度是准确的。离开这个中心点越远，距离和面积的失真就越大。
4. 圆形特征：在等角投影中，经线和纬线通常呈现为从中心点向外辐射的圆形。所有通过中心点的经线都是直线，而纬线则是圆弧。

等角投影常用于以下情况：

• 航海和飞行导航，因为它保持了方向的真实性。
• 表示以某个特定点为中心的区域，例如城市服务区域或军事行动区域。

"形状不变"的含义是，地图上的图形（如三角形）与地球表面上的对应图形在角度和比例上保持一致。例如，如果地球表面上有一个等边三角形，那么在等角投影的地图上，这个三角形也将是等边的，尽管它的面积和形状可能会因为投影而变形。重要的是，所有内部角度和相对边的比例保持不变。

等角投影的一个常见例子是极射赤平投影（Stereographic projection），它将地球表面投影到一个平面上，使得北极或南极成为投影的中心点。这种投影在极地地区特别有用。

Google 等地图为什么选择墨卡托投影

墨卡托投影的“等角”特性，保证了对象的形状的不变行，正方形的物体投影后不会变为长方形。“等角”也保证了方向和相互位置的正确性，因此在航海和航空中常常应用，而Google们在计算人们查询地物的方向时不会出错。墨卡托投影的“圆柱”特性，保证了南北（纬线）和东西（经线）都是平行直线，并且相互垂直。而且经线间隔是相同的，纬线间隔从标准纬线（此处是赤道，也可能是其他纬线）向两级逐渐增大。但是，“等角”不可避免的带来的面积的巨大变形，特别是两极地区，明显的如格陵兰岛比实际面积扩大了N倍。

投影过程

将地球展开成一个圆柱，再将圆柱展开成平面

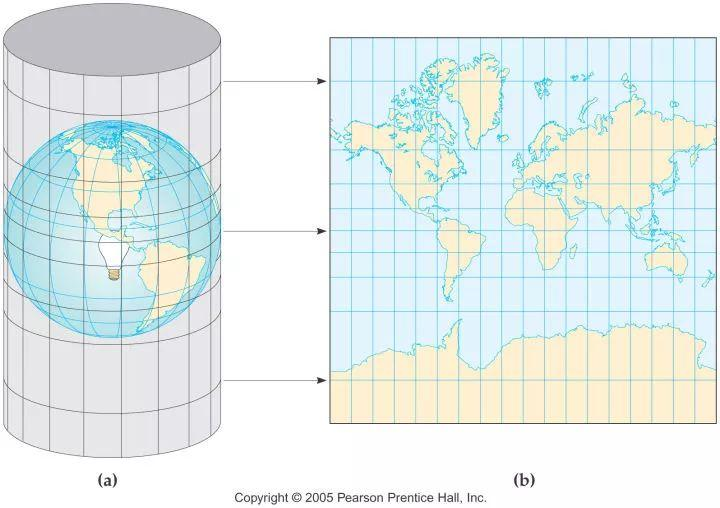
从球心出发射出一条直线，它与球的交点投影后的位置就是这条线与圆柱的交点。

当然，中间的计算过程中会做一些取舍。

从上图中可以看出，X轴的刻度是等距的，Y轴方向越靠近两极变形越大。

墨卡托投影范围

由于墨卡托投影在两极附近是趋于无限值得，因此它并没完整展现了整个世界，地图上最高纬度是 85.05 度。为了简化计算，采用球形映射，而不是椭球体形状。虽然采用墨卡托投影只是为了方便展示地图，需要知道的是，这种映射会给Y轴方向带来0.33%的误差。

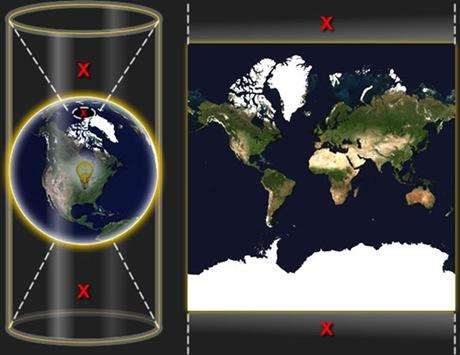
• X轴：

  由于赤道半径为 $6378137$ 米，则赤道周长为 $2\pi r = 20037508.3427892$ 。

  因此 X 轴的取值范围：$[-20037508.3427892,20037508.3427892]$。

• Y轴：

  当纬度 φ 接近两极，即 90° 时，Y 值趋向于无穷。

  因此通常把 Y 轴的取值范围也限定在 $[-20037508.3427892,20037508.3427892]$ 之间。

范围：因此在墨卡托投影坐标系（米）下的坐标范围是：最小为 (-20037508.3427892, -20037508.3427892) 到最大坐标为 (20037508.3427892, 20037508.3427892)。

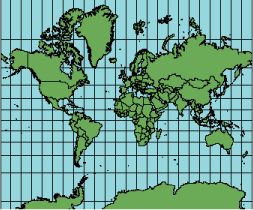
数学计算

下列公式在使用墨卡托投影的地图中，从纬度 φ 和经度 λ (其中 $λ_0$是本初子午线) 推导为坐标系中的坐标 $x$ 和 $y$。

• 古德曼函数的逆推导：

λ, φ -> x, y

$$ \begin{aligned} & \mathrm{x}=\lambda-\lambda_{0} \\ & \mathrm{y}=\ln\left(\tan\left(\frac{\pi}{4}+\frac{\varphi}{2}\right)\right) \\ & =\frac{1}{2}\ln\left(\frac{1+\sin(\varphi)}{1-\sin(\varphi)}\right) \\ & =\tanh^{-1}(\sin(\varphi)) \\ & =\sinh^{-1}(\tan(\varphi)) \\ & =\ln(\tan(\varphi)+\sec(\varphi)). \end{aligned} $$

• 古德曼函数：

x, y -> λ, φ

$$ \begin{array}{c}{{\varphi=2\tan^{-1}(e^{y})-{\frac{\pi}{2}}}}\\ {{=\tan^{-1}(\sinh(y))}}\\ {{\lambda=x+\lambda_{0}.}}\end{array} $$

此处的 $x$ 为坐标 $x / R$， $y$ 为 $y / R$，$R=6378137$

比例尺与纬度 φ 的正割成比例，越趋向极地（φ = ±90°）面积变形越大。此外，由公式可知，极点处的 $y$ 值为正负无穷大。

公式推导

假设地球为正球形。（实际上并非为正球形，而是有扁率的，但制作小比例尺地图时误差可忽略不计。若需更精确，可插入等角纬线。）我们需要将经纬度坐标（λ, φ）转换为笛卡尔坐标(x, y)，求以赤道为基准的切柱面投影（即x = λ），并保持形状不变，故：

$$
\frac{\partial x}{\partial\lambda}=\cos(\varphi)\frac{\partial y}{\partial\varphi}
$$

$$
{\frac{\partial y}{\partial\lambda}}=-\cos(\varphi){\frac{\partial x}{\partial\varphi}}
$$

从 x = λ 可知
$$
\frac{\partial x}{\partial\lambda}=1
$$

$$
{\frac{\partial x}{\partial\varphi}}=0
$$

给出
$$
\cos(\varphi)\frac{\partial y}{\partial\varphi}= 1
$$

$$
{\frac{\partial y}{\partial\lambda}}=0
$$

因此，y 是 φ 的唯一函数，且可得到 $𝑦′=\sec ⁡𝜑$，由积分表
$$
y=\ln(|\sec(\varphi)+\tan(\varphi)|)+C.
$$
在地图中 φ = 0 得到 y = 0，所以取 C = 0.

错觉

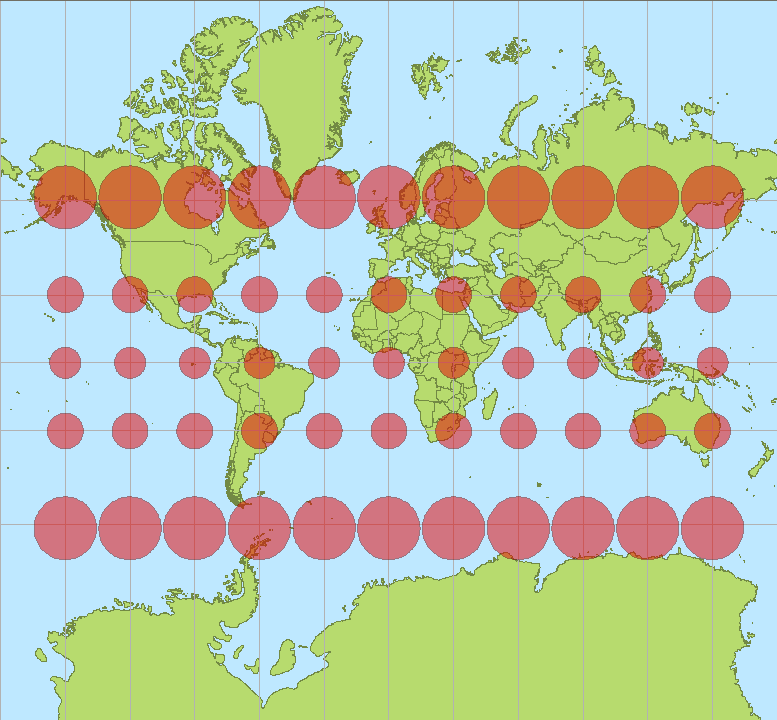
对于墨卡托投影来说，越到高纬度，大小扭曲越严重，到两极会被放到无限大，所以，墨卡托投影无法显示极地地区。下图来自维基百科，可以看到墨卡托投影下每个国家的大小和实际大小的差异。但是 conformality（正形性） 和 straight rhumb lines 这两个特点，让它非常适合于航海导航。

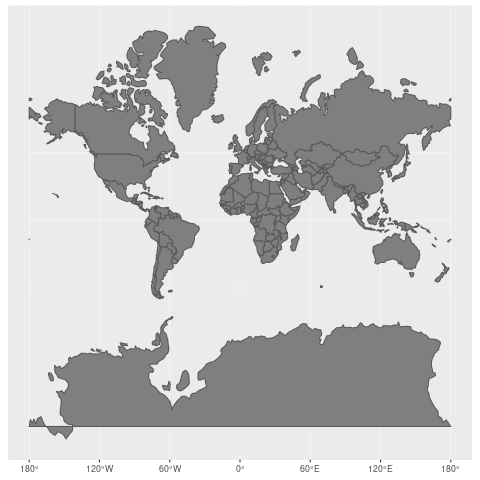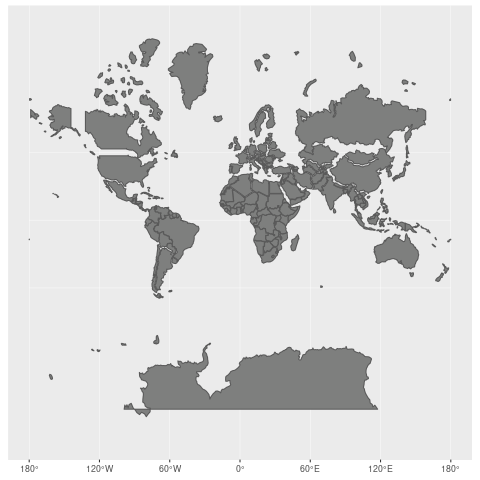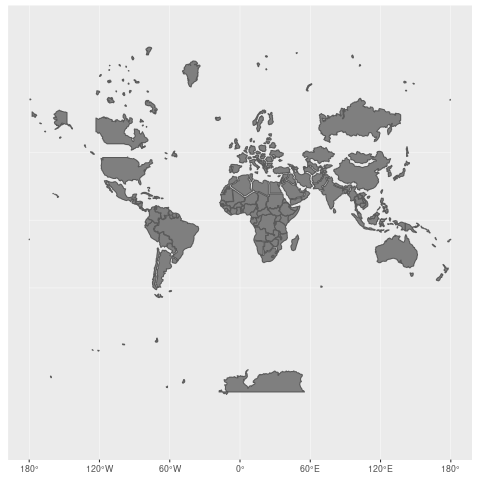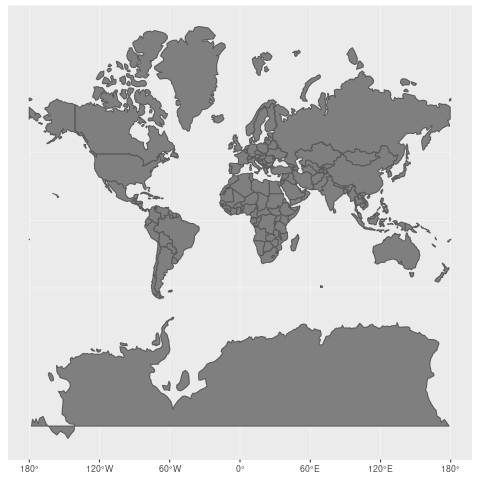
由于麦卡托投影在高纬度过分放大，低纬度又过分缩小，因此会产生有趣的错觉。比如世界第一大岛高纬度的格陵兰比澳洲看起来还大好几倍。世界第二大岛低纬度的新几内亚和日本差不多大小。然而新几内亚岛面积足足是日本的2倍。

参考资料

• https://zh.wikipedia.org/zh-hans/麥卡托投影法
• https://zhuanlan.zhihu.com/p/98951492
• https://zhuanlan.zhihu.com/p/33295151
• https://www.cnblogs.com/arxive/p/7472104.html
• https://bbs.huaweicloud.com/blogs/246214
• https://www.cnblogs.com/gispathfinder/p/6087558.html

文章链接：
https://www.zywvvd.com/notes/study/gis/mercator-proj/mercator-proj/