GIS 概念 - 地理坐标系与投影坐标系

工作中遇到需要用到 GIS 基础知识，本文记录地理坐标和投影坐标系的概念。

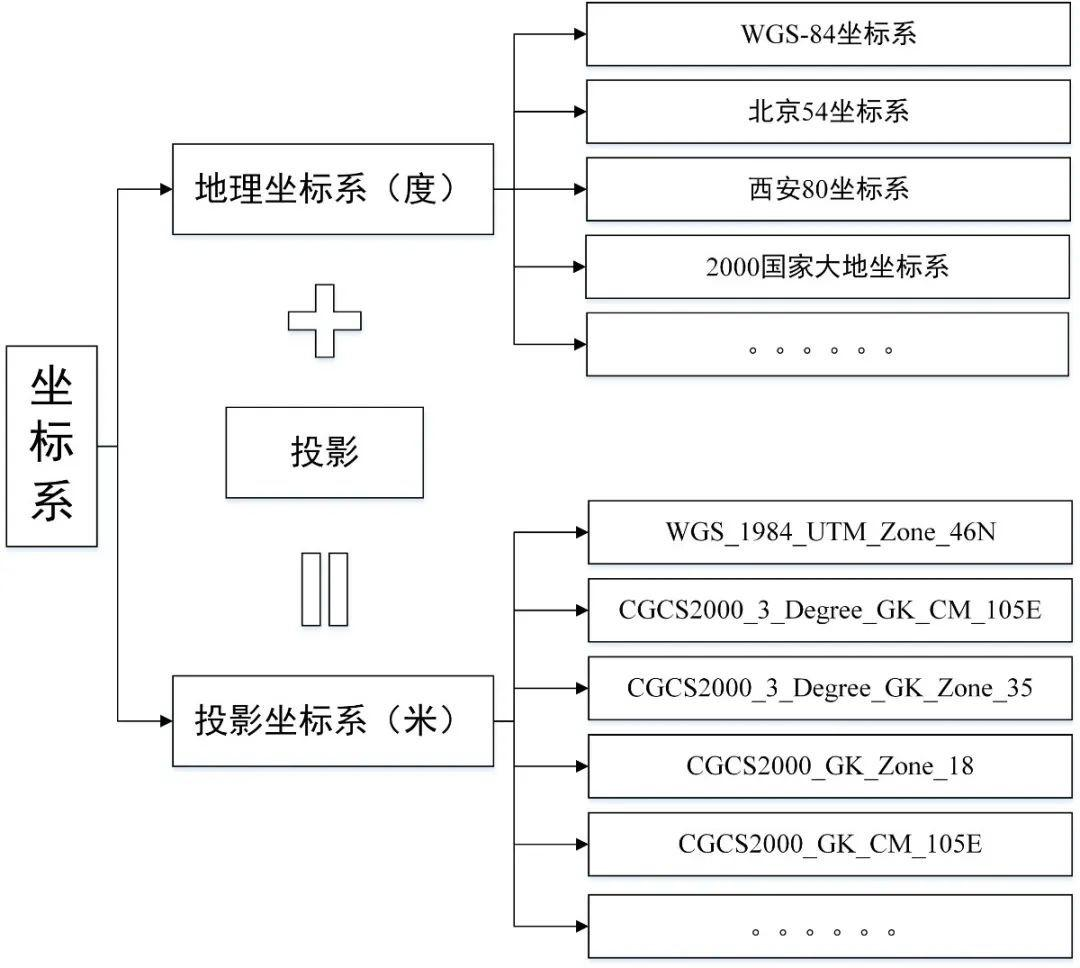
简介

“地理坐标系统”（Geographic Coordinate System，GCS）和"投影坐标系统"（Projected Coordinate System，PCS）是地理信息系统（GIS）中用于描述和定位地球表面上位置的两种不同的坐标系统。

ArcGis 提供了一个可伸缩的、全面的 GIS 平台，具有强大的地图制作、空间数据管理、空间分析、空间信息整合、发布与共享的能力。可以辅助 GIS 学习、开发过程。

	地理坐标系统 (GCS)	投影坐标系统 (PCS)
坐标系	球面坐标系	平面坐标系
参考面	椭球面	水平面
坐标单位	经纬度	米
描述方式	地理坐标系统使用经度和纬度来描述地球表面上的位置。经度表示东西方向上的位置，纬度表示南北方向上的位置。	投影坐标系统使用平面坐标来描述地球表面上的位置，通过将地球表面投影到一个平面上来实现。投影是一种将三维地球表面映射到二维平面上的数学转换。
表达方式	坐标以度、分、秒（DMS）或者十进制度（DD）的形式表示。例如，纽约市的地理坐标可能是经度 -74.0059°，纬度 40.7128°。	坐标通常以米或者英尺为单位表示，可以是直角坐标系（x，y）的形式。例如，通用横轴墨卡托投影（Universal Transverse Mercator，UTM）使用了直角坐标系。
应用范围	主要用于全球性的地理表示，适用于较大范围的地图或空间分析。	主要用于局部地图，适用于小到中等范围的地理表示和测量。

地理坐标系

Geographic coordinate system直译为地理坐标系统，是以经纬度为地图的存储单位的。很明显，Geographic coordinate syst em是球面坐标系统。我们要将地球上的数字化信息存放到球面坐标系统上，用经线（子午线）、纬线、经度、纬度表示地面点位。

地理坐标系一般是指由经度、纬度和高度组成的坐标系，能够标示地球上的任何一个位置。前面提到了，不同地区可能会使用不同的参考椭球体，即使是使用相同的椭球体，也可能会为了让椭球体更好地吻合当地的大地水准面，而调整椭球体的方位，甚至大小。这就需要使用不同的大地测量系统（Geodetic datum）来标识。因此，对于地球上某一个位置来说，使用不同的测量系统，得到的坐标是不一样的。我们在处理地理数据时，必须先确认数据所用的测量系统。事实上，随着我们对地球形状测量的越来越精确，北美使用的 NAD83 基准和欧洲使用的 ETRS89 基准，与 WGS 84 基准是基本一致的，甚至我国的 CGCS2000 与 WGS84 之间的差异也是非常小的。但是差异非常小，不代表完全一致，以 NAD83 为例，因为它要保证北美地区的恒定，所以它与 WGS84 之间的差异在不断变化，对于美国大部分地区来说，每年有1-2cm的差异。

地球是一个不规则的椭球，如何将数据信息以科学的方法存放到椭球上，这必然要求我们找到这样的一个椭球体。这样的椭球体具有特点：可以量化计算的，具有长半轴，短半轴，偏心率。

一般地理坐标可分为三种，天文经纬度，大地经纬度，地心经纬度。通常地图上使用的经纬度都为大地经纬度。

• 大地经度：参考椭球面上某点的大地子午面与本初子午面间的两面角。向东为正，向西为负。

• 大地纬度 ：参考椭球面上某点的法线与赤道平面的夹角。向北为正，向南为负。

• 大地高： 指某点沿法线方向到参考椭球面的距离。

只需要参考椭球体参数以及大地基准面就可以确定地理坐标系。

4326

以 WGS-84地理坐标系为例，定义该坐标系的参数：

GCS_WGS_1984
WKID: 4326 权限:EPSG
Angular Unit: Degree https://e7868a.com/gis-coordinate-project(0.0174532925199433)
Prime Meridian: Greenwich (0.0)
Datum: D_WGS_1984
Spheroid: WGS11984
Semimajor Axis: 6378137.0
Semiminor Axis: 6356752.314245179
Inverse Flattening: 298.257223563

主要就是以下参数：

Prime Meridian（起始经度）
Datum（大地基准面）: D_WGS_1984
Spheroid（参考椭球体）: WGS11984

投影坐标系

在地球椭球面和平面之间建立点与点之间函数关系的数学方法，称为地图投影。这就相当于把地球当成一个橘子，然后一刀切开，把橘子皮平面铺开，这个过程就是地理投影的过程。严谨一点来说就是建立一个参考系统，按照对应位置把椭球体投射到平面。

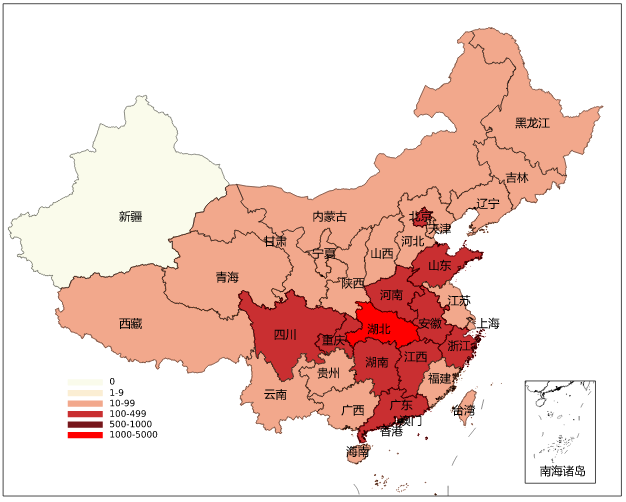
地球椭球表面是一种不可能展开的曲面，要把这样一个曲面表现到平面上，就会发生裂隙或褶皱。在投影面上，可运用经纬线的“拉伸”或“压缩”（通过数学手段）来加以避免，以便形成一幅完整的地图。地图投影的变形通常有：长度变形、面积变形和角度变形。在实际应用中，根据使用地图的目的，限定某种变形。

地理坐标系是三维的，我们要在地图或者屏幕上显示就需要转化为二维，这被称为 投影（Map projection）。显而易见的是，从三维到二维的转化，必然会导致变形和失真，失真是不可避免的，但是不同投影下会有不同的失真，这让我们可以有得选择。常用的投影有 等矩矩形投影（Platte Carre） 和 墨卡托投影（Mercator）。

投影变形

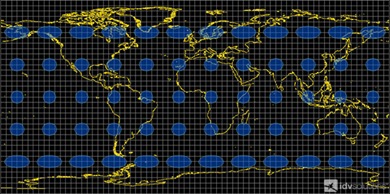
这个例子使用天梭圆来说明墨卡托和等矩矩形投影地球的不同方式。在左边的地球仪上，假设那些蓝色的圆圈是地球上大小和形状相同 (圆形) 的想象中的岛屿。

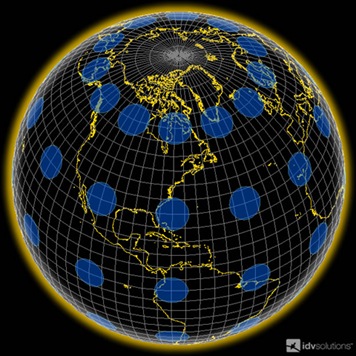
麦卡托投影法非常明显地扭曲了物体的大小，物体离赤道越远就会越大。然而，形状保持不变 —— 那些想象中的蓝色岛屿仍然是圆的。

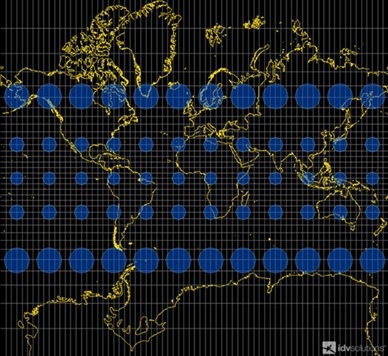
等矩矩形投影的形状发生了变化。具体来说，离赤道越远，被压扁的东西就越多。

国家2000投影坐标系

CGCS2000_3_Degree_GK_CM_l 14E
WKID: 45。权限:EPSG
Projection: Gauss_Kruger
False_Easting: 500000.0
False_Northing: 0.0
Central_Meridian: 114.0
Scale一Factor: 1.0
Latitude_Of_Origin: 0.0
Linear Unit: Meter (1.0)

坐标系分类

按变形性质分类：

• 等角投影：角度变形为零（Mercator），地球面上的图形在投影后保持面积不变

• 等积投影：面积变形为零（Albers），地球面上的图形在投影后保持面积不变

• 任意投影：长度、角度和面积都存在变形，既不具备等角性质，又没有等面积性质的投影。其中一特例是等距离投影，即该投影只在某些特定方向上没有变形

其中，各种变形相互联系相互影响：等积与等角互斥，等积投影角度变形大，等角投影面积变形大。

从投影面类型划分：

• 横圆柱投影：投影面为横圆柱

• 圆锥投影：投影面为圆锥

• 方位投影：投影面为平面

从投影面与地球位置关系划分为：

• 正轴投影：投影面中心轴与地轴相互重合

• 斜轴投影：投影面中心轴与地轴斜向相交

• 横轴投影：投影面中心轴与地轴相互垂直

• 相切投影：投影面与椭球体相切

• 相割投影：投影面与椭球体相割

投影坐标系选择

• 研究区东西跨度较小，数据来源主要为遥感影像

当使用遥感影像作为主要的数据来源时，且研究区域较小时，可以使用UTM投影。由于卫星数据自带投影信息，统一采用卫星影像的投影信息即可

• 研究区东西跨度较小，数据来源为国内地形数据

国内小范围地形数据目前大多采用CGCS2000坐标系，高斯克吕格投影(Gauss-Kruger)。

• 研究区范围大，全国及省区制图

在这种情况下高斯克吕格投影和UTM投影就不再适用了，全国和省区往往跨了好几个3°带甚至6°带，这种情况下高斯克吕格或UTM投影的变形不再可以接受，这时就需要使用阿尔伯斯等面积投影（Albers）或兰伯特正形圆锥投影（Lambert）。

EPSG

EPSG（The European Petroleum Survey Group）发布并维护着一套公用的坐标参考系统（Coordinate System）数据集参数，其坐标参考系统的编码通常称为 EPSG Code，因使用简单而成为最常用的坐标参考系表达方式。

• EPSG 主页：https://epsg.io/
• 各种坐标系参数定义：https://developers.arcgis.com/javascript/3/jshelp/gcs.htm

投影分带

投影分带使用的规定

• 6°：分带在1：2.5万到1：50万时
• 3°：分带在大于1：1万地形图中

带号计算

北半球地区，选择最后字母为“N”的带，南半球“S”

带号=(经度整数位/6)的整数部分+31

带号	经度范围（东经）	中央经线经度
43N	72°-78°	75°
44N	78°-84°	81°
45N	84°-90°	87°
46N	90°-96°	93°
47N	96°-102°	99°
48N	102°-108°	105°
49N	108°-114°	111°
50N	114°-120°	117°
51N	120°-126°	123°
52N	126°-132°	129°
53N	132°-138°	135°

6°分带法

6度带带号=(经度+6°)/6取整

从格林尼治零度经线起,自东半球向西半球, 每经差6°分为一个投影带, 即东经0～6, 6～12, 12～18, ….174～180,用阿拉伯数字1, 2, 3, 4, ….60表示投影带号, 全球共分为60个投影带。

东半球中央经线的计算公式为:

• L0=(6n−3)°
• n表示投影带号，n<30

西半球中央经线的计算公式为:

• L0=(6n−3)°−360°
• n表示投影带号，n>30

3°分带法

3度带带号=(经度+1.5°)/3取整

从东经1°30′算起，自东半球向西半球每3°为一带，将全球划分为120个投影带，1°30′−4°30′,4°30′−7°30′….其中央经线的位置为3°,6°,9°,15°…180°,−177°…−3°

东半球中央经线的计算公式为:

• L0=(3n)°
• n表示投影带号，n<30

西半球中央经线的计算公式为:

• L0=(3n)°−360°
• n表示投影带号，n>30

参考资料

• https://www.cnblogs.com/lishanyang/p/6129856.html
• https://e7868a.com/gis-coordinate-project
• https://blog.csdn.net/whl0071/article/details/126587839
• https://blog.csdn.net/qq_36427942/article/details/136596402
• https://help.supermap.com/iServer/Appendix/CoordSystem/EPSGCode.htm
• https://www.arcgis.net.cn/
• https://idvux.wordpress.com/2007/06/06/mercator-vs-well-not-mercator-platte-carre/
• https://zhuanlan.zhihu.com/p/379610875

文章链接：
https://www.zywvvd.com/notes/study/gis/gis-knowledge-coor/gis-knowledge-coor/