本文最后更新于:2025年4月14日 晚上
本文介绍 Self-Supervised Learning 的原理和合理性,并记录
MoCo系列对SeIf-Supervised Learning领域产生的影响。
简介
-
Self-Supervised Learning,又称为自监督学习,我们知道一般机器学习分为有监督学习,无监督学习和强化学习。而Self-Supervised Learning是无监督学习里面的一种,主要是希望能够学习到一种通用的特征表达用于下游任务 (Downstream Tasks)。 -
其主要的方式就是通过自己监督自己。作为代表作的 Kaiming 的 MoCo 引发一波热议, Yann Lecun 也在 AAAI 上讲
Self-Supervised Learning是未来的大势所趋。 -
MoCo至今已出现了三个版本,第一版MoCo v1是在SimCLR诞生之前的一种比较流行的无监督学习方法,这个系列的前2个工作MoCo v1和v2是针对 CNN 设计的,而MoCo v3是针对Transformer模型设计的,本文主要介绍 Moco v1 的思想喝来源。
Self-Supervised Learning
-
概况来说就是
Unsupervised Pre-train,Supervised Fine-tune -
在预训练阶段我们使用无标签的数据集 (unlabeled data),因为有标签的数据集很贵,打标签得要多少人工劳力去标注,那成本是相当高的。无标签的数据相对便宜。
-
在训练模型参数的时候,我们不追求把这个参数用带标签数据从初始化的一张白纸给一步训练到位,原因就是数据集太贵。于是 Self-Supervised Learning 就想先把参数从 一张白纸 训练到 初步成型,再从 初步成型 训练到 完全成型。注意这是2个阶段。
-
这个训练到初步成型的东西,我们把它叫做
Visual Representation。预训练模型的时候,就是模型参数从 一张白纸 到 初步成型 的这个过程,还是用无标签数据集。等我把模型参数训练个八九不离十,这时候再根据你 下游任务 (Downstream Tasks) 的不同去用带标签的数据集把参数训练到 完全成型,那这时用的数据集量就不用太多了,因为参数经过了第1阶段就已经训练得差不多了。 -
第1个阶段不涉及任何下游任务,就是拿着一堆无标签的数据去预训练,没有特定的任务,这个话用官方语言表达叫做:in a task-agnostic way。第2个阶段涉及下游任务,就是拿着一堆带标签的数据去在下游任务上 Fine-tune,这个话用官方语言表达叫做:in a task-specific way

-
自监督学习的关键可以概括为两点:Pretext Task,Loss Function
MoCo 系列也遵循这个思想,预训练的 MoCo 模型也会得到 Visual Representation,它们可以通过 Fine-tune 以适应各种各样的下游任务,比如检测和分割等等。MoCo在 7 个检测/语义分割任务(PASCAL VOC, COCO, 其他的数据集)上可以超过他的有监督训练版本。有时会超出很多。这表明在有监督与无监督表示学习上的差距在许多视觉任务中已经变得非常近了。
自监督学习的 Pretext Task
- Pretext Task 是无监督学习领域的一个常见的术语,其中 “Pretext” 翻译过来是"幌子,托词,借口"的意思。所以 Pretext Task 专指这样一种任务:这种任务并非我们所真正关心的,但是通过完成它们,我们能够学习到一种很好的表示,这种表示对下游任务很重要。
BERT
-
在训练 BERT 的时候,我们曾经在预训练时让它作填空的任务,详见:科技猛兽:Self-Supervised Learning 超详细解读 (一):大规模预训练模型BERT
-
训练时把这段输入文字里面的一部分随机盖住。就是直接用一个Mask把要盖住的token (对中文来说就是一个字)给Mask掉,具体是换成一个特殊的字符。接下来把这个盖住的token对应位置输出的向量做一个Linear Transformation,再做softmax输出一个分布,这个分布是每一个字的概率。因为这时候BERT并不知道被 Mask 住的字是 “湾” ,但是我们知道啊,所以损失就是让这个输出和被盖住的 “湾” 越接近越好。
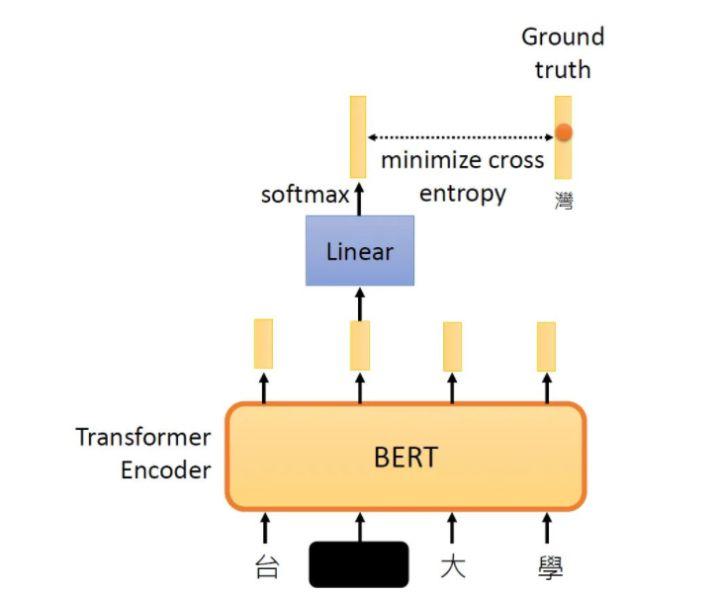
-
通过这种方式训练 BERT,得到的预训练模型在下游任务只要稍微做一点 Fine-tune,效果就会比以往有很大的提升。
-
所以这里的 Pretext Task 就是填空的任务,这个任务和下游任务毫不相干,甚至看上去很笨,但是 BERT 就是通过这样的 Pretext Task学习到了很好的 Language Representation,很好地适应了下游任务。
SimCLR
- 在训练 SimCLR 的时候,我们曾经在预训练时试图教模型区分相似和不相似的事物。
- 假设现在有1张任意的图片 ,叫做Original Image,先对它做数据增强,得到2张增强以后的图片 。接下来把增强后的图片输入到Encoder 里面,注意这2个Encoder是共享参数的,得到representation ,再把 继续通过 Projection head 得到 representation ,这里的2个 Projection head 依旧是共享参数的,且其具体的结构表达式是:
$$
z_{i}=g\left(h_{i}\right)=W^{(2)} \sigma\left(W^{(1)} h_{i}\right)
$$
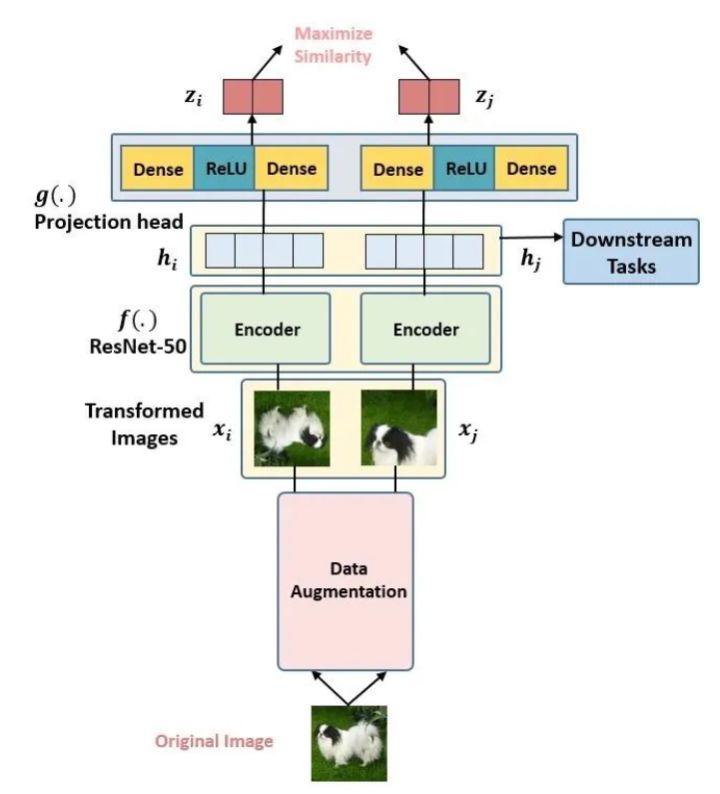
- 通过这种方式训练 SimCLR,得到的预训练模型在下游任务只要稍微做一点 Fine-tune,效果就会比以往有很大的提升。
- 这里的 Pretext Task 就是试图教模型区分相似和不相似的事物,这个任务和下游任务毫不相干,甚至看上去很笨,但是 SimCLR 就是通过这样的 Pretext Task学习到了很好的 Image Representation,很好地适应了下游任务。
还有一些常见的 Pretext Task 诸如 denoising auto-encoders,context autoencoders,cross-channel auto-encoders等等。
Before MoCo
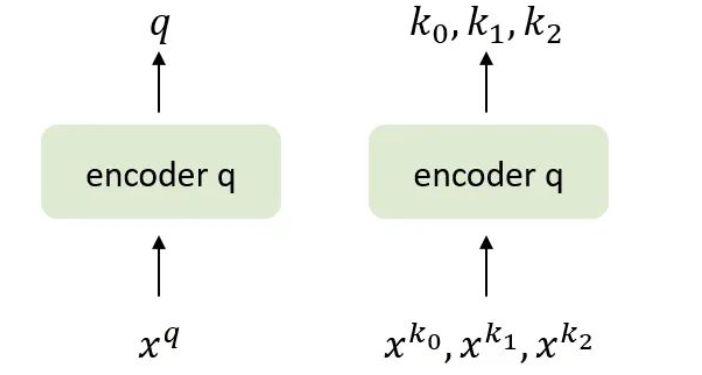
-
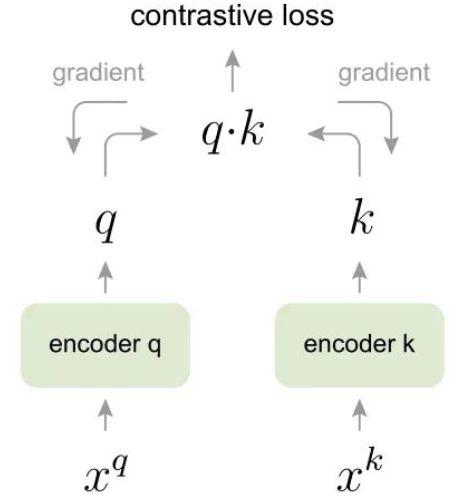
考虑图中的网络,输入通过编码器 Encoder 得到 query ,还有几个输入 通过编码器 Encoder 得到 key 。假设只有一个 key 和 是匹配的。根据上面的 Contrastive loss 的性质,只有当 和相匹配的 相近,且与其他不匹配的 相远时, Contrastive loss 的值才会最小。这个工作使用点积作为相似度的度量,且使用 InfoNCE 作为Contrastive loss,则有:
$$ \mathcal{L}_{q}=-\log \frac{\exp \left(q \cdot k_{+} / \tau\right)}{\sum_{i=0}^{K} \exp \left(q \cdot k_{i} / \tau\right)} $$ -
我们定义与 q 相似 / 匹配的样本为正样本,反之为负样本,假设 batch size = 256,那么对于给定的一个样本 ,选择一个正样本 (这里正样本的对于图像上的理解就是 的 data augmentation版本)。然后选择256个负样本 (对于图像来说,就是除了 之外的图像),然后使用 loss function 来将与正样本之间的距离拉近,负样本之间的距离推开。
-
batch size 越大效果越好的,这一点在 SimCLR 中也得到了证明。但是,由于算力的影响 batch size 不能设置过大,因此很难应用大量的负样本。因此效率较低。
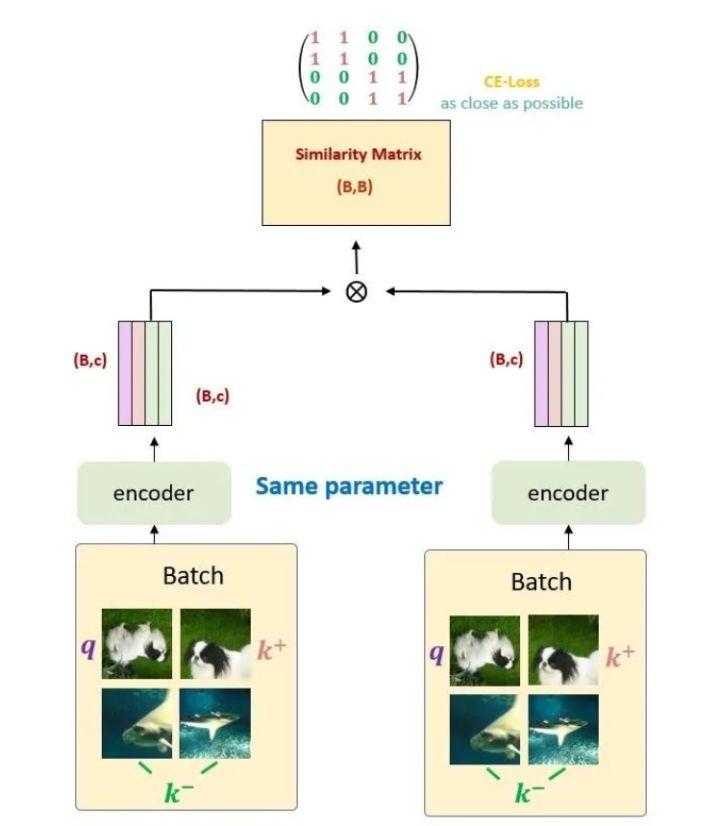
原始的端到端自监督学习方法
- 针对很难应用大量的负样本的问题,下面给出了一种方案
采用一个较大的memory bank存储较大的字典
-
对于给定的一个样本 ,选择一个正样本 (这里正样本的对于图像上的理解就是 的 data augmentation版本)。采用一个较大的 memory bank 存储较大的字典,这个 memory bank 具体存储的是所有样本的representation。(涵盖所有的样本,比如样本一共有60000个,那么memory bank大小就是60000,字典大小也是60000),采样其中的一部分负样本 ,然后使用 loss function 来将与正样本之间的距离拉近,负样本之间的距离推开。这次只更新 Encoder 的参数,和几个采样的key值 。因为这时候没有了 Encoder 的反向传播,所以支持memory bank容量很大。
-
但是,你这一个step更新的是 Encoder 的参数,和几个采样的key值 ,下个step更新的是 Encoder 的参数,和几个采样的key值 ,问题是 ,也就是:Encoder 的参数每个step都更新,但是某一个 key 可能很多个step才被采样到更新一次,而且一个epoch只会更新一次。这就出现了一个问题,即:每个step编码器都会进行更新,这样最新的 query 采样得到的 key 可能是好多个step之前的编码器编码得到的 key,因此丧失了一致性。

-
从这一点来看,[1 原始的端到端自监督学习方法] 的一致性最好,但是受限于batchsize的影响。而 [2 采用一个较大的memory bank存储较大的字典] 的字典可以设置很大,但是一致性却较差,这看起来似乎是一个不可调和的矛盾。
MoCo
kaiming大神利用 momentum (移动平均更新模型权重) 与queue (字典) 轻松的解决这个问题。

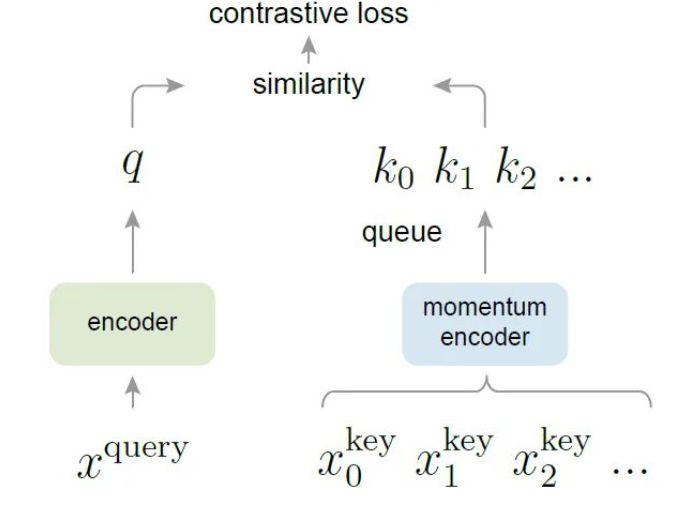
- 首 先 我 们 假 $ K(K>N) $ ,注意这里 $ K $ 一般是 $ N $ 的数倍,比如 $ K=3 N, K=5 N, \ldots $ ,但是 $ K $ 总 是比 $ N $ 要大的 (代码里面 $ K=65536 $ ,即队列大小实际是65536)。
- 如图中所示,有俩网络,一个是 Encoder ,另一个是Momentum Encoder 。这两个模型的网络结构是一样的,初始参数也是一样的 (但是训练开始后两者参数将不再一样了)。$ f_{\mathrm{q}} $ 与 $ f_{\mathrm{Mk}} $ 是将输入信息映射到特征空间的网络,特征空间由一个长度为 $C$ 的向量表示,它们分别表示为:f_q , f_k 和 C。
- k 可以看作模板,q看作查询元素,每一个输入未知图像的特征由f_q提取,现在给一系列由f_k提取的模板特征(比如狗的特征、猫的特征),就能使用f_q与f_k的度量值来确定f_q是属于什么。
算法流程
-
现在我们有一堆无标签的数据,拿出一个 Batch,表示为 $ \mathbf{x} $ ,也就是 $ N $ 张图片,分别进行两种不同的数据增强,得到 x_q 和 x_k ,则x_q是 $ N $ 张图片, x_k 也是 $ N $ 张图片。
1
2
3for x in loader: # 输入一个图像序列x,包含N张图,没有标签
x_q = aug(x) # 用于查询的图 (数据增强得到)
x_k = aug(x) # 模板图 (数据增强得到),自监督就体现在这里,只有图x和x的数据增强才被归为一类 -
分别通过Encoder和Momentum Encoder:
-
x_q 通过 Encoder 得到特征 $ \mathbf{q} $ ,维度是 $ N, C $ ,这里特征空间由一个长度为 $ C=128 $ 的 向量表示。
-
x_k 通过 Momentum Encoder 得到特征 $ \mathbf{k} $ ,维度是 $ N, C $ 。
1
2q = f_q.forward(x_q) # 提取查询特征,输出NxC
k = f_k.forward(x_k) # 提取模板特征,输出NxC -
-
Momentum Encoderl的参数不更新:
1
2# 不使用梯度更新f_k的参数,这是因为文章假设用于提取模板的表示应该是稳定的,不应立即更新
k.detach() -
计算N张图片的自己与自己的增强图的特征的匹配度:
1
2# 这里bmm是分批矩阵乘法
1_pos = bmm(q.view(N, 1, C), k.view(N, C, 1)) # 输出Nx1,也就是自己与自己的增强图的特征的匹配度这里得到的I_pos的维度是**(N,1,1), N个数代表N**张图片的自己与自己的增强图的特征的匹配度。
-
计算N张图片与队列中的K张图的特征的匹配度:
1
1_neg = mm(q.view(N, C), queue.view(C, K) # 输出Nxk,自己与上一批次所有图的匹配度(全不匹配)这里得到的I_neg的维度是**(N,K),代表N张图片与队列 Queue 中的K**张图的特征的匹配度。
-
把4,5两步得到的结果concat起来:
1
logits = cat([1_pos, 1_neg], dim=1) # 输出 N x (1+k)这里得到的 logits 的维度是 (N, K+1),把它看成是一个矩阵的话呢,有 N 行,代表一个 Batch里面的 N 张图片。每一行的第1个元素是某张图片自己与自己的匹配度,每一行的后面K 个元素是某张图片与其他 K 个图片的匹配度,下图展示的是某一行的信息,这里的 K=2。

每一行的第1个元素是某张图片自己与自己的匹配度,每一行的后面K 个元素是某张图片与其他 K 个图片的匹配度
-
NCE损失函数,就是为了保证自己与自己衍生的匹配度输出越大越好,否则越小越好:
1
2
3
4labels = zeros(N)
# NCE损失函数,就是为了保证自己与自己衍生的匹配度输出越大越好,否则越小越好
loss = CrossEntropyLoss(logits/t, labels)
loss.backward() -
更新 Encoder 的参数:
1 | |
- Momentum Encoder 的参数使用动量更新:
1 | |
- 更新队列,删除最老的一个 Batch,加入一个新的 Batch:
1 | |
- 全部的伪代码 (来自MoCo的paper):
1 | |
FAQ
- Encoder $ f_{\mathrm{q}} $ 和 Momentum Encoder $ f_{\mathrm{Mk}} $ 的输入分别是什么?
Encoder $ f_{\mathrm{q}} $ 的输入是一个Batch的样本 $ \mathbf{x} $ 的增强版本 x__q。 Momentum Encoder $ f_{\mathrm{Mk}} $ 的输入是一个 Batch 的样本 $ \mathbf{x} $ 的另一个增强版本 和 队列x_k Momentum Encoder 得到代码中的变量 queue。
- Encoder $ f_{\mathrm{q}} $ 和 Momentum Encoder $ f_{\mathrm{Mk}} $ 的更新方法有什么不同?
Encoder $ f_{\mathrm{q}} $ 在每个 step 都会通过反向传播更新参数,假设 1 个 epoch 里面有500 个 step,Encoder $ f_{\mathrm{q}} $ 就更新 500次。Momentum Encoder $ f_{\mathrm{Mk}} $在每个 step 都会通过动量的方式更新参数,假设 1 个 epoch 里面有500 个 step,Momentum Encoder $ f_{\mathrm{Mk}} $ 就更新 500次,只是更新的方式是:
$$
\theta_{\mathrm{k}} \leftarrow m \theta_{\mathrm{k}}+(1-m) \theta_{\mathrm{q}}
$$
式中, $ m $ 是动量参数,默认取 $ m=0.999 $ ,这意味着 Momentum Encoder的更新是极 其缓慢的,而且并不是通过反向传播来更新参数,而是通过动量的方式来更新。
- MoCo 相对于原来的两种方法的优势在哪里?
在 [1 原始的端到端自监督学习方法] 里面,Encoder $ f_{\mathrm{q}} $ 和 Encoder $ f_{\mathrm{k}} $ 的参数每个s tep 都更新,这个问题在前面也有提到,因为Encoder $ f_{\mathrm{k}} $ 输入的是一个 Batch 的 negativ e samples,所以输入的数量不能太大,即dictionary不能太大,即 Batch size不能太大。
现在的 Momentum Encoder $ f_{\mathrm{Mk}} $ 的更新是以动量的方法更新的,不涉及反向传播,所以 $ f_{\mathrm{Mk}} $ 输入的负样本 (negative samples) 的数量可以很多,具体就是 Queue 的大 小 可 以 比 较 大 , 那当然是负样本的数量越多越好了。这就是 Dictionary as a queue 的含义,即通过动量更新的形式,使得可以包含更多的负样本。而且 Momentum Encoder $ f_{\mathrm{Mk}} $ 的更新极其缓慢 (因为 $ m=0.999 $ 很接近于1),所以Momentum Encoder $ f_{\mathrm{Mk}} $ 的更新相当于是看了很多的 Batch,也就是很多负样本。
在 [2 采用一个较大的memory bank存储较大的字典] 方法里面,所有样本的 representa tion 都存在 memory bank 里面,根据上文的描述会带来最新的 query 采样得到的 key 可能是好多个step之前的编码器编码得到的 key,因此丧失了一致性的问题。但是MoCo的 每个step都会更新Momentum Encoder,虽然更新缓慢,但是每个step都会通过动量更新 一下Momentum Encoder,这样 Encoder $ f_{\mathrm{q}} $ 和 Momentum Encoder $ f_{\mathrm{Mk}} $ 每个step 都有更新,就解决了一致性的问题。
实验
-
Encoder的具体结构是 ResNet,Contrastive loss 的超参数 $ \tau=0.07 $。
-
数据增强的方式是 (都可以通过 Torchvision 包实现):
-
Randomly resized image + random color jittering
-
Random horizontal flip
-
Random grayscale conversion
-
-
作者还把 BN 替换成了 Shuffling BN,因为 BN 会欺骗 pretext task,轻易找到一种使得 loss 下降很快的方法。
-
自监督训练的数据集是:ImageNet-1M (1280000 训练集,各类别分布均衡) 和 Instagram-1B (1 billion 训练集,各类别分布不均衡)
-
优化器:SGD,weight decay: 0.0001,momentum: 0.9。
-
Batch size:N=256
-
初始学习率:0.03,200 epochs,在第120和第160 epochs时分别乘以0.1,结束时是0.0003。
实验一:Linear Classification Protocol
-
评价一个自监督模型的性能,最关键和最重要的实验莫过于 Linear Classification Protocol 了,它也叫做 Linear Evaluation,具体做法就是先使用自监督的方法预训练 Encoder,这一过程不使用任何 label。预训练完以后 Encoder 部分的权重也就确定了,这时候把它的权重 freeze 住,同时在 Encoder 的末尾添加Global Average Pooling和一个线性分类器 (具体就是一个FC层+softmax函数),并在某个数据集上做Fine-tune,这一过程使用全部的 label。
-
上述方法 [1 原始的端到端自监督学习方法],[2 采用一个较大的memory bank存储较大的字典],[3 MoCo方法] 的结果对比如下图所示。
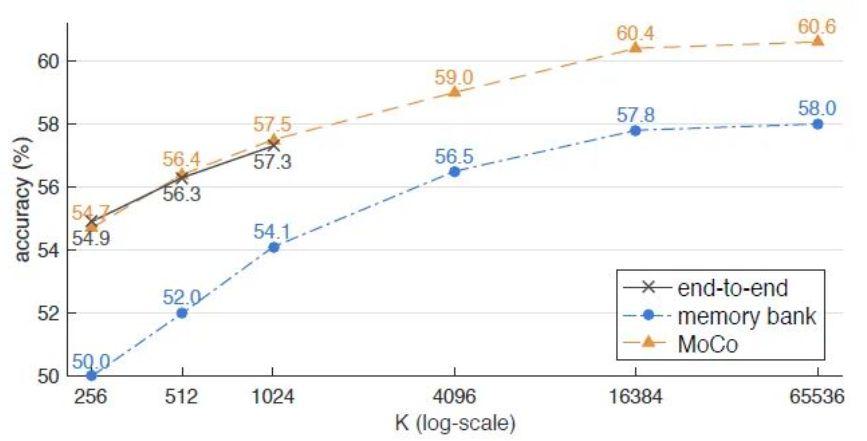
- 图中的 K:
-
对于[3 MoCo方法] 来讲就是队列Queue的大小,也是负样本的数量。
-
对于[1 原始的端到端自监督学习方法] 是一个 Batch 的大小,那么这种方法的一个Batch 有 1 个正样本和 K-1 个负样本。因为对于给定的一个样本 $ x^{q} $ ,选择一个 正样本 $ x^{k_{+}} $(这里正样本的对于图像上的理解就是 $ x^{q} $ 的 data augmentation版本)。然后选择一批负样本 (对于图像来说,就是除了 $ x^{q} $ 之外的图像),样本 $ x^{q} $ 输入 给 Encoder $ f_{\mathrm{q}} $ ,正样本和负样本都输入给 Encoder $ f_{\mathrm{k}} $ ,所以有 $ \mathrm{K}-1 $ 个负样本。
-
对于 [2 采用一个较大的memory bank存储较大的字典] 方法来讲,也是负样本的 数量。
- 我们看到图中的3条曲线都是随着 的增加而上升的,证明对于每一个样本来讲,正样本的数量都是一个,随着负样本数量的上升,自监督训练的性能会相应提升。我们看图10中的黑色线 最大取到了1024,因为这种方法同时使用反向传播更新Encoder 和 Encoder 的参数,所以 Batch size 的大小受到了显存容量的限制。同时橙色曲线是最优的,证明了MoCo方法的有效性。
实验二: 对比不同动量参数 $ m $
-
结果如下图11所示, $ m $ 取0.999时性能最好,当 $ m =0$ 时,即 Momentum Encoder $ f_{\mathrm{Mk}} $ 参数 $ \theta_{\mathrm{k}} \leftarrow \theta_{\mathrm{q}} $ ,即直接拷贝Encoder $ f_{\mathrm{q}} $ 的参数,则训练失败,说明 2 个网络的参数不 可以完全一致。
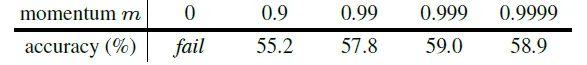
实验三: 与其他方法对比
-
如下图所示,设置 $ K=65536, m=0.999 $ ,Encoder 架构是 ResNet-50,MoCo可 以达到 $ 60.6 % $ 的准确度,如果 ResNet-50 的宽度设为原来的 4 倍,则精度可以进一步达到 $ 68.6 % $ ,比以往方法更占优。

实验四:下游任务 Fine-tune 结果
-
有了预训练好的模型,我们就相当于是已经把参数训练到了初步成型,这时候再根据下游任务 (Downstream Tasks) 的不同去用带标签的数据集把参数训练到 完全成型,那这时用的数据集量就不用太多了,因为参数经过了第1阶段就已经训练得差不多了。
-
本文的下游任务是:PASCAL VOC Object Detection 以及 COCO Object Detection and Segmentation,主要对比的对象是 ImageNet 预训练模型 (ImageNet supervised pre-training),注意这个模型是使用100%的 ImageNet 标签训练的。
PASCAL VOC Object Detection 结果
-
实验设置
-
Backbone: Faster R-CNN: R50-dilated-C5 或者 R50-C4。
-
训练数据尺寸:训练时 [480, 800],推理时 800。
-
Evaluation data:即测试集是 VOC test2007 set。
-
-
如下图是在 trainval07+12 (约16.5k images) 数据集上 Fine-tune 之后的结果,当Backbone 使用 R50-dilated-C5 时,在 ImageNet-1M 上预训练的 MoCo 模型的性能与有监督学习的性能是相似的。在 Instagram-1B 上预训练的 MoCo 模型的性能超过了有监督学习的性能。当Backbone 使用 R50-dilated-C5 时,在 ImageNet-1M 或者 Instagram-1B 上预训练的 MoCo 模型的性能都超过了有监督学习的性能。
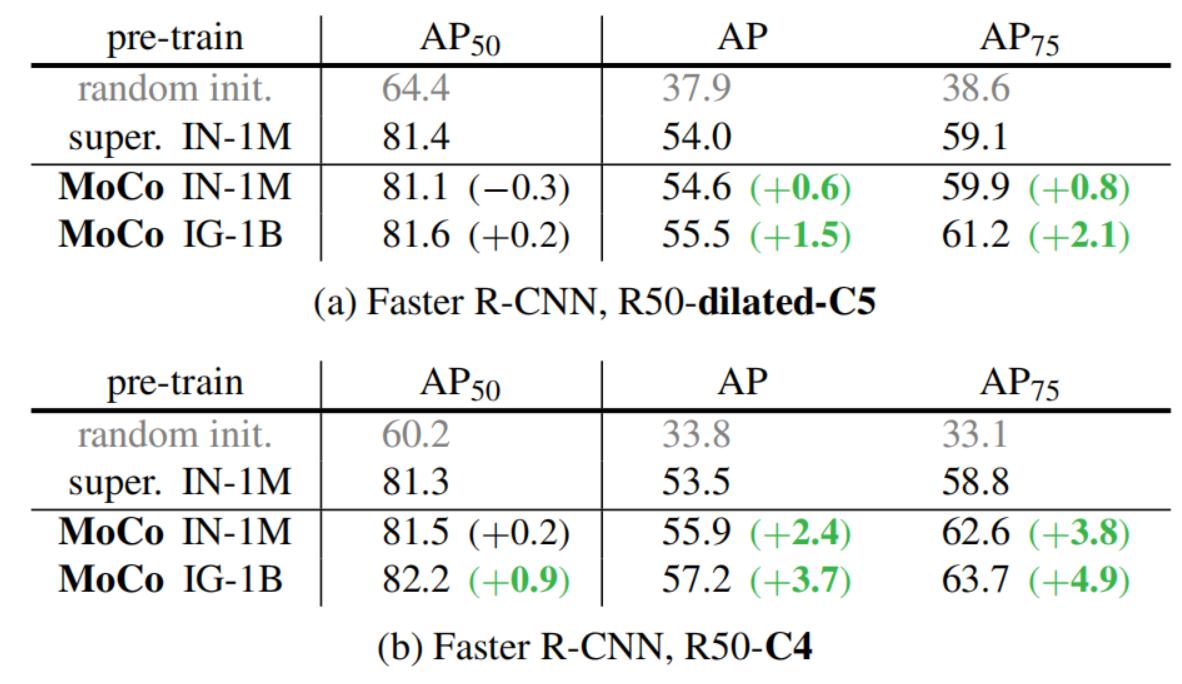
-
接着作者又在下游任务上对比了方法1,2 和 MoCo 的性能,如下图所示。end-to-end 的方法 (上述方法1) 和 memory bank 方法 (上述方法2) 的性能都不如MoCo。
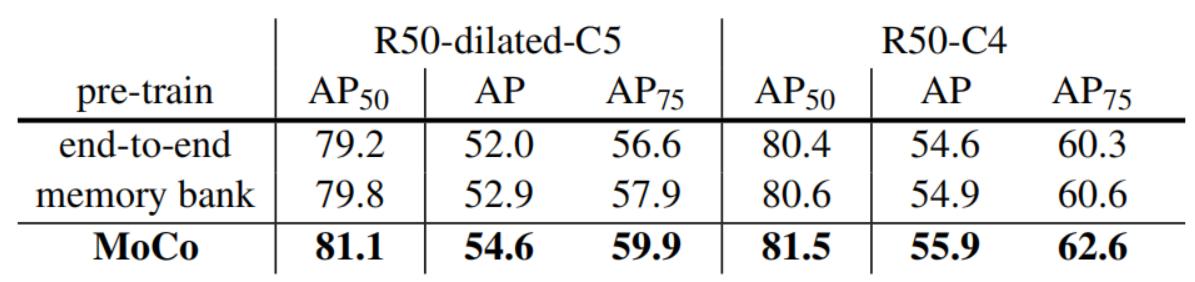
原始论文
参考资料
- http://www.360doc.com/content/21/0816/00/32196507_991221821.shtml
- https://zhuanlan.zhihu.com/p/469100381
- http://dljz.nicethemes.cn/news/show-17095.html
文章链接:
https://www.zywvvd.com/notes/study/deep-learning/moco/moco/
“觉得不错的话,给点打赏吧 ୧(๑•̀⌄•́๑)૭”

微信支付

支付宝支付