表征学习 Contrastive Loss

对比学习中一般使用 Contrastive Loss 作为损失函数，这种损失函数可以有效的处理孪生神经网络中的 paired data 的关系。

Contrastive Loss

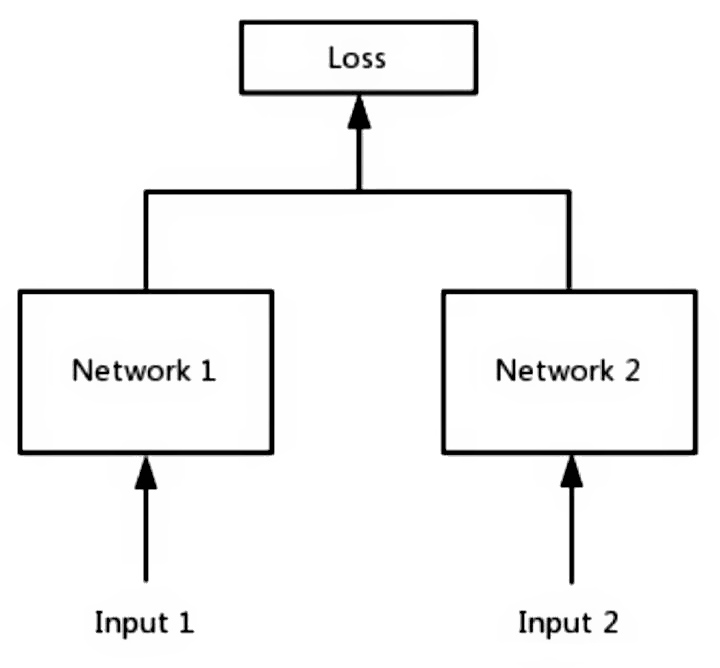
• 这种损失函数最初来源于 Yann LeCun 的 《Dimensionality Reduction by Learning an Invariant Mapping》，主要是用在降维中，即本来相似的样本，在经过降维（特征提取）后，在特征空间中，两个样本仍旧相似；而原本不相似的样本，在经过降维后，在特征空间中，两个样本仍旧不相似。

  

• 这种损失函数可以有效的处理孪生神经网络中的paired data的关系（形式上并不一定是两个Net，也可以是一个Net两个Out，可以认为上面示意图的 Network1 和 2 是同一个，或者不是同一个）。

• 表达式如下：

$$
L=\frac{1}{2 N} \sum_{n=1}^{N} y d^{2}+(1-y) \max (\operatorname{margin}-d, 0)^{2}
$$

• 其中$ d=\left|a_{n}-b_{n}\right|_{2} $ 代表两个样本特征的欧氏距离，$y$为两个样本是否匹配的标签，$y=1$代表两个样本相似或者匹配，$y=0$则代表不匹配，margin为设定的阈值。

• 观察上述的 contrastive loss 的表达式可以发现，这种损失函数可以很好的表达成对样本的匹配程度，也能够很好用于训练提取特征的模型。当 $y=1$（即样本相似）时，损失函数只剩下 $∑yd^2$，即原本相似的样本，如果在特征空间的欧式距离较大，则说明当前的模型不好，因此加大损失。而当 $y=0$ 时（即样本不相似）时，损失函数为 $(1-y) \max (\operatorname{margin}-d, 0)^{2}$，即当样本不相似时，其特征空间的欧式距离反而小的话，损失值会变大，这也正好符号我们的要求。

  

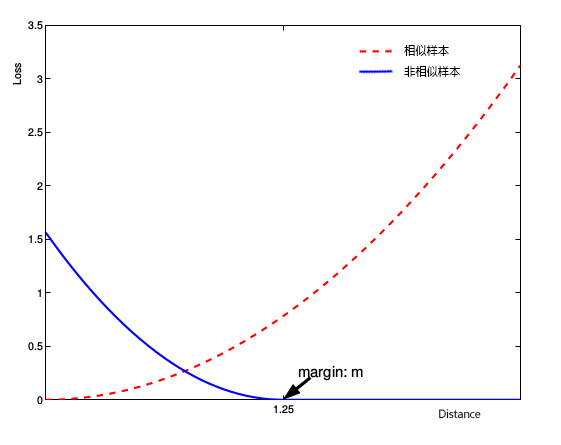
弹簧模型类比

• 弹簧模型公式：
  $$
  F=-KX
  $$

  F表示两点间弹簧的作用力，K是弹簧的劲度系数，X为弹簧拉伸或收缩的长度，弹簧静止状态时X=0.

• 论文中将该contrastive loss损失函数类比于弹簧模型：将成对的样本特征，使用该损失函数来表达成对样本特征的匹配程度。成对的样本特征之间（类比于图中的一个个点），我们假设这些点之间都有一个弹簧，弹簧静止时长度为０，点对之间无作用力。

  1. 对于样本相似的特征，相当于其间的弹簧产生了正位移Ｘ(X < m)，即弹簧被拉伸了X的长度，此时两个相似特征（点）之间存在吸引力。
  2. 对于样本不相似的特征，相当于其间的弹簧产生的了负位移，即弹簧被压缩了，此时两个不相似特征之间存在排斥力。注意弹簧的特性：当两点之间弹簧位移超Ｘ>m时，此时，弹簧发生形变，此时两点之间视为没有吸引力了。

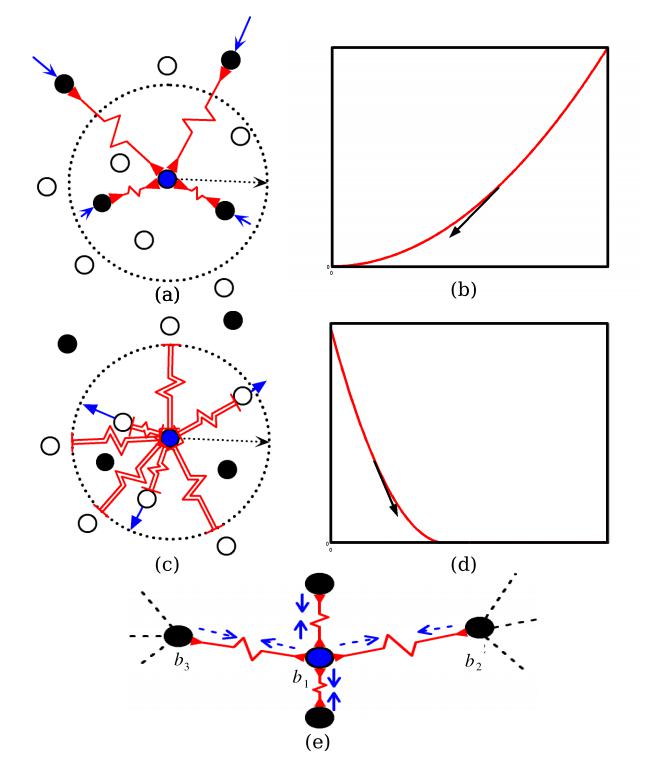
• 黑色样本表示和中心相似的样本，空心样本表示和中心不相似的样本。这些弹簧显示为红色的锯齿形线。作用在这些点上的力用蓝色箭头表示。箭头的长度近似地给出了力的强度。

  1. 显示使用仅吸引弹簧与类似点连接的点。

  2. 损失函数及其梯度与相似的对相关。

  3. 仅与半径m圆内的不同点相连。

  4. 显示了与不同的对相关的损失函数及其梯度。

  5. 显示一个点被其他点在不同方向上拉动，创造平衡的情况。

原始论文

### 参考资料

• https://www.jianshu.com/p/21be99fb58ca
• https://blog.csdn.net/autocyz/article/details/53149760
• https://xubin.blog.csdn.net/article/details/104723588?spm=1001.2101.3001.6661.1&utm_medium=distribute.pc_relevant_t0.none-task-blog-2~default~CTRLIST~default-1-104723588-blog-53149760.pc_relevant_scanpaymentv1&depth_1-utm_source=distribute.pc_relevant_t0.none-task-blog-2~default~CTRLIST~default-1-104723588-blog-53149760.pc_relevant_scanpaymentv1&utm_relevant_index=1
• https://www.jianshu.com/p/21be99fb58ca
• https://blog.csdn.net/forever__1234/article/details/81222092

文章链接：
https://www.zywvvd.com/notes/study/deep-learning/contrastive-loss/contrastive-loss/