重参数化技巧 - 连续分布采样

本文最后更新于：2024年5月7日下午

重参数化（Reparameterization）技巧是一种在机器学习和统计学中常用的技术，主要用于将一个随机变量转换成另一个随机变量，同时保证它们的概率分布保持不变，在生成模型中有着重要应用。

简介

重参数化技巧，就是从一个分布 $ p_{\theta}(z) $ 中进行采样，而该分布是带有参数 ${\theta}$ 的，如果直接进行采样（采样动作是离散的，其不可微），是没有梯度信息的，那么在BP反向传播的时候就不会对参数梯度进行更新。重参数化技巧可以保证我们从 $ p_{\theta}(z) $ 进行采样，同时又能保留梯度信息。

连续分布采样

我们考虑以下形式:
$$
J_{\theta}=\int p_{\theta}(z) f(z) d z
$$
其中 $ p_{\theta}(z) $ 可以是任何分布，假如是高斯分布。直接求解上述等式中积分形式通常是不可能的，所以需要进行采样。

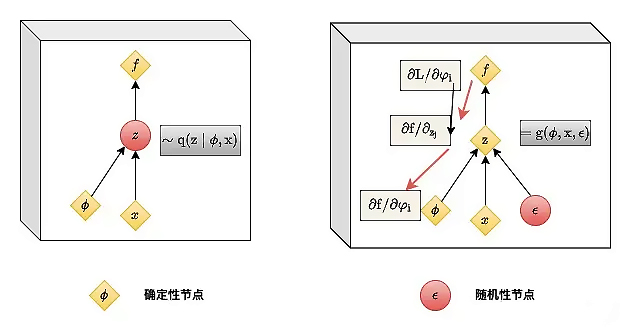
重参数化技巧，左图没进行重参数化，右图是进行了重参数化

图中， $x$ 表示高斯分布的均值， $ \phi $ 表示标准差，他们是确定性节点，而需要输出的隐变量 $z$ 是带有随机性的节点，重参数技巧就是把带有随机性的节点变成确定性的节点，将随机性转移出计算图用另一个输入节点 $ \varepsilon $ 进行随机性采样。原本从 $ N\left(x, \phi^{2}\right) $ 中采样得到 $z$ 。将其转化成从标准正态分布 $N(0,1)$ 中采样得到 $ \varepsilon $ ，从而 $ z=x+\varepsilon \cdot \phi $ 。这样就解决了采样导致梯度不可传递的问题。
$$
\begin{aligned} J_{\theta} & =\mathbb{E}{z \sim \mathcal{N}\left(z ; \mu{\theta}, \sigma 2\right)}[f(z)] \ & =\mathbb{E}{\varepsilon \sim q(\varepsilon)}\left[f\left(g{\theta}(\varepsilon)\right)\right] \ & =\mathbb{E}{\varepsilon \sim \mathcal{N}(\varepsilon ; 0,1)}\left[f\left(\varepsilon \times \sigma{\theta}+\mu_{\theta}\right)\right]\end{aligned}
$$