本文最后更新于:2024年5月7日 下午
重参数化也可以用在离散分布采样中,由于对我来说相比于连续分布的重参数技巧,离散重参数难理解很多,本文单独介绍离散部分的重参数化 。
简介
这篇文章从直观感觉讲起,先讲Gumbel-Softmax Trick用在哪里及如何运用,再编程感受Gumbel分布的效果,最后讨论数学证明。

问题来源
通常在强化学习中,如果动作空间是离散的,比如上、下、左、右四个动作,通常的做法是网络输出一个四维的one-hot向量(不考虑空动作),分别代表四个动作。比如 [1,0,0,0] 代表上,[0,1,0,0] 代表下等等。而具体取哪个动作呢,就根据输出的每个维度的大小,选择值最大的作为输出动作,即 $arg \max (v) $ .
例如网络输出的四维向量为 $v=[−20,10,9.6,6.2]$,第二个维度取到最大值 10,那么输出的动作就是 [0,1,0,0],也就是说,这和多类别的分类任务是一个道理。但是这种取法有个问题是不能计算梯度,也就不能更新网络。通常的做法是加softmax函数,把向量归一化,这样既能计算梯度,同时值的大小还能表示概率的含义。softmax函数定义如下:
$$ \sigma\left(z_{i}\right)=\frac{e^{z_{i}}}{\sum_{j=1}^{K} e^{z_{j}}} $$那么将 v=[−20,10,9.6,6.2] 通过softmax函数后有 $σ(v)=[0,0.591,0.396,0.013]$,这样做不会改变动作或者说类别的选取,同时 softmax 倾向于让最大值的概率显著大于其他值,比如这里10和9.6经过 softmax 放缩之后变成了 0.591 和 0.396,6.2 对应的概率更是变成了 0.013,这有利于把网络训成一个 one-hot 输出的形式,这种方式在分类问题中是常用方法。
但是这么做还有一个问题,这个表示概率的向量 $σ(v)=[0,0.591,0.396,0.013]$ 并没有真正显示出概率的含义,因为一旦某个值最大,就选择相应的动作或者分类。比如 $σ(v)=[0,0.591,0.396,0.013]$ 和 $σ(v)=[0,0.9,0.1,0]$ 在类别选取的结果看来没有任何差别,都是选择第二个类别,但是从概率意义上讲差别是巨大的。所以需要一种方法不仅选出动作,而且遵从概率的含义。
很直接的方法是依概率分布采样就完事了,比如直接用np.random.choice函数依照概率生成样本值,这样概率就有意义了。这样做确实可以,但是又有一个问题冒了出来:这种方式怎么计算梯度?不能计算梯度怎么用 BP 的方式更新网络?
这时重参数(re-parameterization)技巧解决了这个问题,这里有详尽的解释,不过比较晦涩。简单来说重参数技巧的一个用处是把采样的步骤移出计算图,这样整个图就可以计算梯度BP更新了。之前我一直在想分类任务直接softmax之后BP更新不就完事了吗,为什么非得采样。后来看了VAE和GAN之后明白,还有很多需要采样训练的任务。这里举简单的VAE(变分自编码器)的例子说明需要采样训练的任务以及重参数技巧,详细内容来自视频和博客。
Re-parameterization Trick
最原始的自编码器通常长这样:
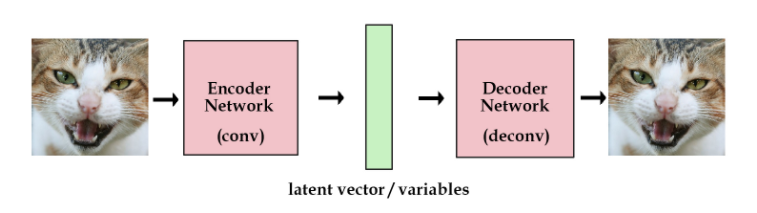
左右两边是端到端的出入输出网络,中间的绿色是提取的特征向量,这是一种直接从图片提取特征的方式。
而 VAE 长这样:
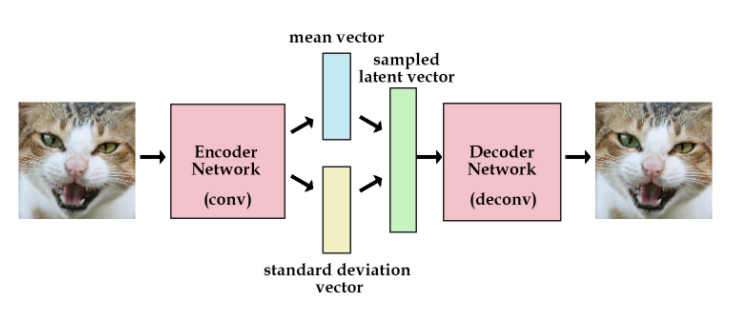
VAE的想法是不直接用网络去提取特征向量,而是提取这张图像的分布特征,也就把绿色的特征向量替换为分布的参数向量,比如说均值和标准差。然后需要decode图像的时候,就从encode出来的分布中采样得到特征向量样本,用这个样本去重建图像,这时怎么计算梯度的问题就出现了。
重参数技巧可以解决这个问题,它长下面这样:

假设图中的 $x$ 和 $ϕ$ 表示 VAE 中的均值和标准差向量,它们是确定性的节点。而需要输出的样本 $z$ 是带有随机性的节点,重参数就是把带有随机性的 $z$ 变成确定性的节点,同时随机性用另一个输入节点 $ϵ$ 代替。例如,这里用正态分布采样,原本从均值为 $x$ 和标准差为 $ϕ$ 的正态分布 $N(x,ϕ2)$ 中采样得到 $z$。将其转化成从标准正态分布 $N(0,1)$中采样得到 $ϵ$,再计算得到 $z=x+ϵ⋅ϕ$ 。这样一来,采样的过程移出了计算图,整张计算图就可以计算梯度进行更新了,而新加的 $ϵ$ 的输入分支不做更新,只当成一个没有权重变化的输入。
到这里,需要采样训练的任务实例以及重参数技巧基本有个概念了。
Gumbel-Max trick
VAE 的例子是一个连续分布(正态分布)的重参数,离散分布的情况也一样,首先需要可以采样,使得离散的概率分布有意义而不是只取概率最大的值,其次需要可以计算梯度。那么怎么做到的,具体操作如下:
对于 $n$ 维概率向量 $π$ ,对 $π$ 对应的离散随机变量 $x_π$ 添加 $Gumbel$ 噪声,再取样:
$$
x_{\pi}=\arg \max \left(\log \left(\pi_{i}\right)+G_{i}\right)
$$
其中,$G_i$ 是独立同分布的标准 Gumbel 分布的随机变量,标准 Gumbel 分布的 CDF 为 $F(x)=e{-e{-x}} $。
这就是 Gumbel-Max trick。
Gumbel-Softmax Trick
可以看到 Gumbel-Max trick 中间有一个 argmax 操作,这是不可导的,所以用 softmax 函数代替,这就是 Gumbel-Softmax Trick 而 $G_i$ 可以通过Gumbel分布求逆从均匀分布生成,即:
$$
G_{i}=-\log \left(-\log \left(U_{i}\right)\right), U_{i} \sim U(0,1)
$$
具体实践
-
对于网络输出的一个 $n$ 维向量 $v$,生成 $n$ 个服从均匀分布 $U(0,1)$ 的独立样本 $ϵ_1,…,ϵ_n$
-
通过 $G_i=−log(−log(ϵ_i))$ 计算得到 $G_i$
-
对应相加得到新的值向量 $v′=[v_1+G_1,v_2+G_2,…,v_n+G_n]$
-
通过 softmax 函数
$$ \sigma_{\tau}\left(v_{i}^{\prime}\right)=\frac{e^{v_{i}^{\prime} / \tau}}{\sum_{j=1}^{n} e^{v_{j}^{\prime} / \tau}} $$
计算概率大小得到最终的类别。其中 $τ$ 是温度参数。
直观上感觉,对于强化学习来说,在选择动作之前加一个扰动,相当于增加探索度,感觉上是合理的。对于深度学习的任务来说,添加随机性去模拟分布的样本生成,也是合情合理的。
Gumbel分布采样效果
为什么使用Gumbel分布生成随机数,就能模拟离散概率分布的样本呢?这部分使用代码模拟来感受它的优越性。这部分例子和代码来自这里。
Gumbel分布的概率密度函数:
$$ p(x)=\frac{1}{\beta} e^{-z-e^{-z}} $$其中 $ z=\frac{x-\mu}{\beta} $ 。
极值分布
Gumbel分布是一类极值分布,那么它表示什么含义呢?
这里举一个类似的喝水的例子。
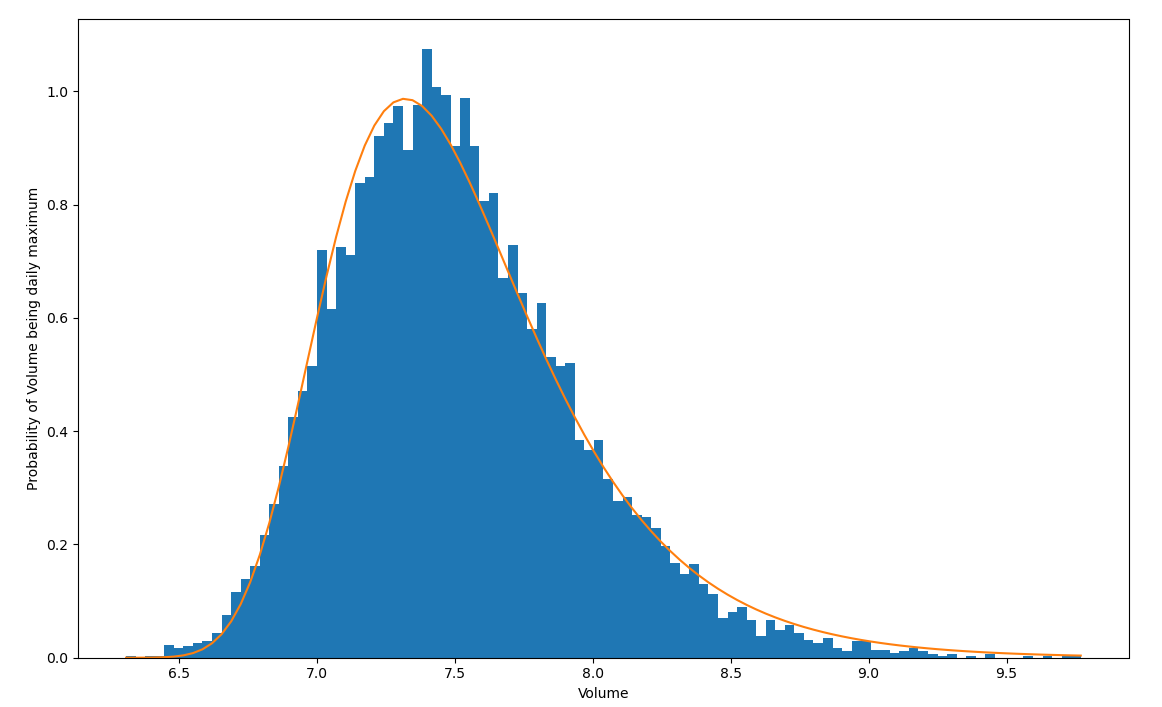
比如你每天都会喝很多次水(比如100次),每次喝水的量也不一样。假设每次喝水的量服从正态分布 $N(μ,σ_2)$ (其实也有点不合理,毕竟喝水的多少不能取为负值,不过无伤大雅能理解就好,假设均值为5),那么每天100次喝水里总会有一个最大值,这个最大值服从的分布就是Gumbel分布。实际上,只要是指数族分布,它的极值分布都服从Gumbel分布。那么上面这个例子的分布长什么样子呢,作图有:
1 | |
那么gumbel分布在离散分布的采样中效果如何呢?可以作图比较一下。先定义一个多项分布,作出真实的概率密度图。再通过采样的方式比较各种方法的效果。
如下代码定义了一个7类别的多项分布,其真实的密度函数如下图
1 | |
1 | |
真实分布
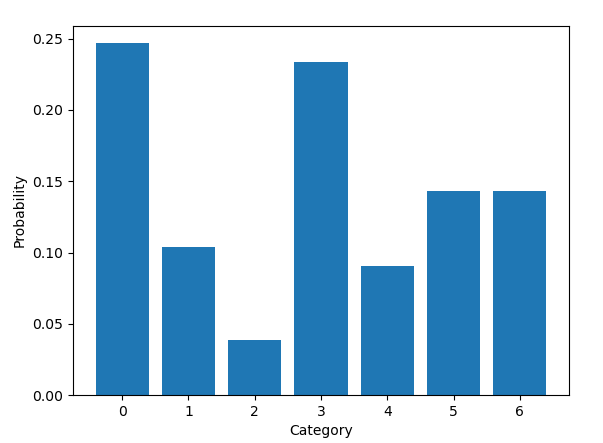
随机采样,就是真实分布
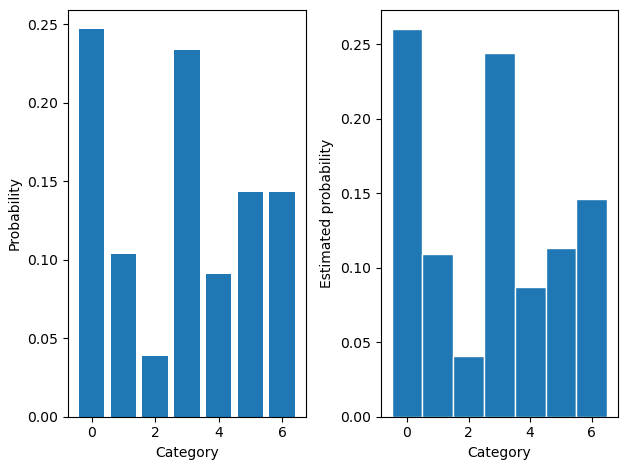
要是没有不能求梯度这个问题,直接从原分布采样是再好不过的。
接着通过前述的方法添加Gumbel噪声采样,同时也添加正态分布和均匀分布的噪声作对比
1 | |
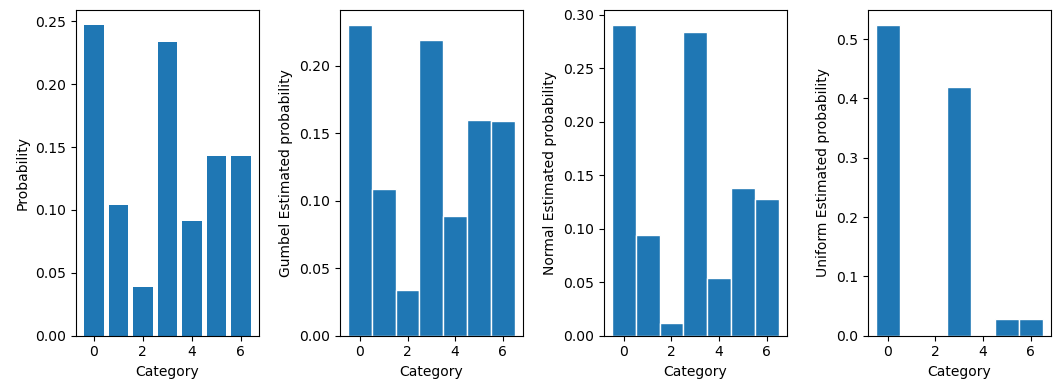
1 | |
可以明显看到Gumbel噪声的采样效果是最好的,正态分布其次,均匀分布最差。也就是说可以用Gumbel分布做Re-parameterization使得整个图计算可导,同时样本点最接近真实分布的样本。
数学证明
为什么添加 Gumbel 噪声有如此效果,下面阐述问题并给出证明。
假设有一个 $K$ 维的输出向量,每个维度的值记为 $x_k$,通过 softmax 函数可得,取到每个维度的概率为:
$$ \pi_{k}=\frac{e^{x_{k}}}{\sum_{k^{\prime}=1}^{K} e^{x_{k^{\prime}}}} $$这是直接 softmax 得到的概率密度函数,如果换一种方式,对每个 $x_k$ 添加独立的标准 Gumbel 分布(尺度参数为1,位置参数为0)噪声,并选择值最大的维度作为输出,得到的概率密度同样为 $π_k$。
下面给出Gumbel分布的概率密度函数和分布函数,并证明这件事情。
尺度参数为1,位置参数为 $μ$ 的Gumbel分布的PDF为:
$$ f(z ; \mu)=e^{-(z-\mu)-e^{-(z-\mu)}} $$ CDF为 $$ F(z ; \mu)=e^{-e^{-(z-\mu)}} $$假设第$k $个Gumbel分布对应 $x_k$,加和得到随机变量 $z_k=x_k+G_k$,即相当于 $z_k$ 服从尺度参数为1,位置参数为 $μ=x_k$的 Gumbel分布。要证明这样取得的随机变量 $z_k$与原随机变量相同,只需证明取到 $z_k$ 的概率为 $π_k$。也就是 $z_k$比其他所有 $z_{k′}(k′≠k)$大的概率为 $π_k$,即:
$$ P\left(z_{k} \geq z_{k^{\prime}} ; \forall k^{\prime} \neq k \mid\left\{x_{k^{\prime}}\right\}_{k^{\prime}=1}^{K}\right)=\pi_{k} $$ 关于 $z_k$ 的条件累积概率分布函数为 $$ \begin{array}{c}P\left(z_{k} \geq z_{k^{\prime}} ; \forall k^{\prime} \neq k \mid z_{k},\left\{x_{k^{\prime}}\right\}_{k^{\prime}=1}^{K}\right)=P\left(z_{1} \leq z_{k}\right) P\left(z_{2} \leq z_{k}\right) \cdots P\left(z_{k-1} \leq z_{k}\right) P\left(z_{k+1} \leq z_{k}\right) \cdots \\ \cdot P\left(z_{K} \leq z_{k}\right)\end{array} $$ 即: $$ P\left(z_{k} \geq z_{k^{\prime}} ; \forall k^{\prime} \neq k \mid z_{k},\left\{x_{k^{\prime}}\right\}_{k^{\prime}=1}^{K}\right)=\prod_{k^{\prime} \neq k} e^{-e^{-\left(z_{k}-x_{k^{\prime}}\right)}} $$ 对 $z_k$ 求积分可得边缘累积概率分布函数 $$ P\left(z_{k} \geq z_{k^{\prime}} ; \forall k^{\prime} \neq k \mid\left\{x_{k^{\prime}}\right\}_{k^{\prime}=1}^{K}\right)=\int P\left(z_{k} \geq z_{k^{\prime}} ; \forall k^{\prime} \neq k \mid z_{k},\left\{x_{k^{\prime}}\right\}_{k^{\prime}=1}^{K}\right) \cdot f\left(z_{k} ; x_{k}\right) d z_{k} $$ 带入式子有 $$ P\left(z_{k} \geq z_{k^{\prime}} ; \forall k^{\prime} \neq k \mid\left\{x_{k^{\prime}}\right\}_{k^{\prime}=1}^{K}\right)=\int \prod_{k^{\prime} \neq k} e^{-e^{-\left(z_{k}-x_{k}\right)}} \cdot e^{-\left(z_{k}-x_{k}\right)-e^{-\left(z_{k}-x_{k}\right)}} d z_{k} $$ 化简有 $$ \begin{array}{l}P\left(z_{k} \geq z_{k^{\prime}} ; \forall k^{\prime} \neq k \mid\left\{x_{k^{\prime}}\right\}_{k^{\prime}=1}^{K}\right) \\ =\int \prod_{k^{\prime} \neq k} e^{-e^{-\left(z_{k}-x_{k^{\prime}}\right)}} \cdot e^{-\left(z_{k}-x_{k}\right)-e^{-\left(z_{k}-x_{k}\right)}} d z_{k} \\ =\int e^{-\sum_{k^{\prime} \neq k} e^{-\left(z_{k}-x_{k^{\prime}}\right)}-\left(z_{k}-x_{k}\right)-e^{-\left(z_{k}-x_{k}\right)}} d z_{k} \\ =\int e^{-\sum_{k^{\prime}=1}^{K} e^{-\left(z_{k}-x_{k^{\prime}}\right)}-\left(z_{k}-x_{k}\right)} d z_{k} \\ =\int e^{-\left(\sum_{k^{\prime}=1}^{K} e^{x^{\prime}}\right) e^{-z_{k}-z_{k}+x_{k}}} d z_{k} \\ =\int e^{-e^{-z_{k}+\ln \left(\sum_{k^{\prime}=1}^{K} e^{\left.x_{k^{\prime}}\right)}\right.}-z_{k}+x_{k}} d z_{k} \\ =\int e^{-e^{-\left(z_{k}-\ln \left(\sum_{k^{\prime}=1}^{K} e^{x_{k^{\prime}}}\right)\right)}-\left(z_{k}-\ln \left(\sum_{k^{\prime}=1}^{K} e^{x_{k^{\prime}}}\right)\right)-\ln \left(\sum_{k^{\prime}=1}^{K} e^{x_{k^{\prime}}}\right)+x_{k}} d z_{k} \\ =e^{-\ln \left(\sum_{k^{\prime}=1}^{K} e^{x_{k^{\prime}}}\right)+x_{k}} \int e^{-e^{-\left(z_{k}-\ln \left(\sum_{k^{\prime}=1}^{K} e^{\left.x_{k^{\prime}}\right)}\right)\right.}-\left(z_{k}-\ln \left(\sum_{k^{\prime}=1}^{K} e^{x_{k^{\prime}}}\right)\right)} d z_{k} \\ =\frac{e^{x_{k}}}{\sum_{k^{\prime}=1}^{K} e^{x_{k^{\prime}}}} \int e^{-e^{-\left(z_{k}-\ln \left(\sum_{k^{\prime}=1}^{K} e^{x_{k^{\prime}}}\right)\right)}-\left(z_{k}-\ln \left(\sum_{k^{\prime}=1}^{K} e^{x_{k^{\prime}}}\right)\right)} d z_{k} \\ =\frac{e^{x_{k}}}{\sum_{k^{\prime}=1}^{K} e^{x_{k^{\prime}}}} \int e^{-\left(z_{k}-\ln \left(\sum_{k^{\prime}=1}^{K} e^{x_{k^{\prime}}}\right)\right)-e^{-\left(z_{k}-\ln \left(\sum_{k^{\prime}=1}^{K} e^{x_{k^{\prime}}}\right)\right)}} d z_{k} \\\end{array} $$ 积分里面是 $ \mu=\ln \left(\sum_{k^{\prime}=1}^{K} e^{x_{k^{\prime}}}\right) $ 的Gumbel分布,所以整个积分为1。则有 $$ P\left(z_{k} \geq z_{k^{\prime}} ; \forall k^{\prime} \neq k \mid\left\{x_{k^{\prime}}\right\}_{k^{\prime}=1}^{K}\right)=\frac{e^{x_{k}}}{\sum_{k^{\prime}=1}^{K} e^{x_{k^{\prime}}}} $$ 这和softmax的结果一致。参考资料
- https://www.cnblogs.com/initial-h/p/9468974.html
- https://casmls.github.io/general/2017/02/01/GumbelSoftmax.html
- http://amid.fish/humble-gumbel
文章链接:
https://www.zywvvd.com/notes/study/deep-learning/generation/reparameterized/repara2/repara2/
“觉得不错的话,给点打赏吧 ୧(๑•̀⌄•́๑)૭”

微信支付

支付宝支付