本文最后更新于:2024年5月7日 下午
扩散模型 (Diffusion Models) 是近年提出的生成模型, 扩散模型已经被证明可以生成高质量的图像,并且相比于GAN能够更好地覆盖样本分布, 本文介绍相关内容。
背景
- 在文章 《Diffusion Models Beat GANs on Image Synthesis》 中展示了扩散模型的图像生成能力:

- 在清晰度、多样性上都不逊色于 GAN 等模型
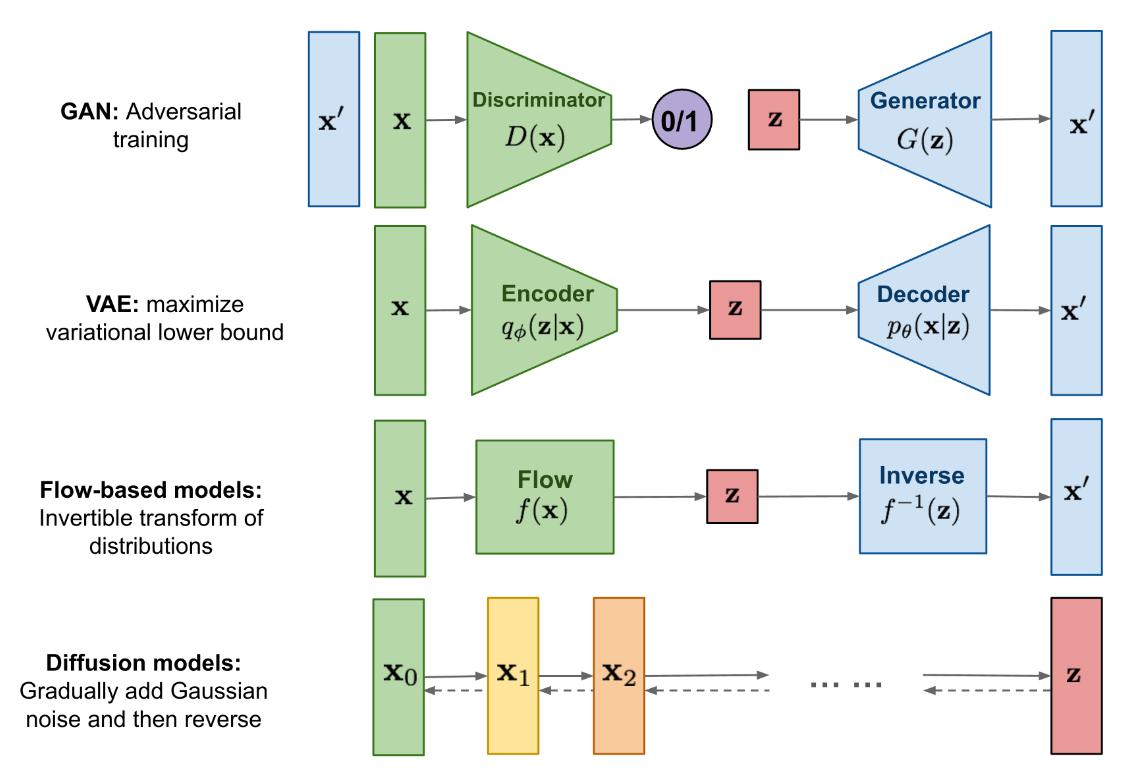
- 扩散模型的灵感来源于非平衡态热力学。他们定义了一个马尔可夫链的扩散步骤,慢慢地向数据中添加随机噪声,然后学习逆向扩散过程,从噪声中构造所需的数据样本。与 VAE 或流动模型不同,扩散模型的学习过程是固定的,隐变量具有较高的维数(与原始数据相同)。
框架
- 扩散模型定义很简单,包含有两个过程,分别为扩散过程和逆扩散过程。

- $ q\left(\mathbf{x} _ {t} \mid \mathbf{x} _ {t-1}\right) $ 是正向扩散过程中的条件概率分布,是我们已知的(通过我们预先设定好的超参数指定好的,不需要用网络去学或者预测)。
- $ p_{\theta}\left(\mathbf{x} _ {t-1} \mid \mathbf{x} _ {t}\right) $ 是逆向重构过程中的条件概率分布,是我们不知道的(极其难获得的),我们要用一个网络去学这个条件概率分布。
- 正向和逆向每一步的条件概率都建模为高斯分布,区别是:正向的高斯分布的均值和方差都是已知的(事先定义好的超参数),而逆向的均值和方差是需要用网络去预测的。
扩散过程
-
给定一个初始数据分布 $ \mathbf{x} _ {0} \sim q(\mathbf{x}) $ (说白了就是训练集),核心过程如上图所示,扩散过程为从右到左 $X_0 \to X_T$ 的过程,表示对图片逐渐加噪。
-
不断向该分布中添加高斯噪声,一共加 $T$ 次,所添加噪声的均值是由预先确定的超参数 $ \beta_{t} $ 所确定的,方差是由 $ \beta_{t} $ 和当前 $t$ 时刻的数据 $x_t$ 所决定的,其中 $ \left\{\beta_{\mathrm{t}} \in(0,1)\right\} _ {\mathrm{t}=1}^{\mathrm{T}} $.
-
加噪过程中经历 $T$ 个状态,每个加噪过程相互独立,即 $ \mathrm{X} _ {t+1} $ 是在 $ X_{t} $ 上加躁得到的,其只受 $ X_{t} $ 的影响, 因此扩散过程是一个马尔科夫过程。
-
$X_0$ 表示从真实数据集中采样得到的一张图片,对 $X_0$ 添加 $T$ 次噪声,图片逐渐变得模糊,当 $T$ 足够大时,$X_T$ 为标准正态分布。
-
在训练过程中,每次添加的噪声是已知的, 即 $ \mathrm{q}\left(\mathrm{X} _ {\mathrm{t}} \mid \mathrm{X} _ {\mathrm{t}-1}\right) $ 是已知的,根据马尔科夫过程的性质,我们可以递归得到 $ \mathrm{q}\left(\mathrm{X} _ {\mathrm{t}} \mid \mathrm{X} _ {0}\right) $ ,即 $ \mathrm{q}\left(\mathrm{X} _ {\mathrm{t}} \mid \mathrm{X} _ {0}\right) $ 是已知的。
-
$ q\left(X_{t} \mid X_{t-1}\right) $ 可写为如下形式,即给定 $ \mathrm{X} _ {\mathrm{t}-1} $ 的条件下, $ \mathrm{X} _ {\mathrm{t}} $ 服从均值为 $ \sqrt{1-\beta_{t}} X_{t-1} $ ,方差为 $ \beta_{t} $ 的正态分布:
$$
q\left(X_{t} \mid X_{t-1}\right)=N\left(X_{t} ; \sqrt{1-\beta_{t}} X_{t-1}, \beta_{t} I\right)
$$ -
用重参数化技巧表示$ X_{t}$ ,令 $ \alpha_{t}=1-\beta_{t} $ ,令 $ Z_{t} \sim N(0, I), \mathrm{t} \geq 0 $ , 即:
$$ \begin{array}{c} \mathrm{X} _ {\mathrm{t}}&=&\sqrt{\alpha_{\mathrm{t}}} \mathrm{X} _ {\mathrm{t}-1}+\sqrt{1-\alpha_{\mathrm{t}}} \mathrm{Z} _ {\mathrm{t}-1}\\ \mathrm{X} _ {\mathrm{t}-1}&=&\sqrt{\alpha_{\mathrm{t}-1}} \mathrm{X} _ {\mathrm{t}-2}+\sqrt{1-\alpha_{\mathrm{t}-1}} \mathrm{Z} _ {\mathrm{t}-2} \\ \mathrm{X} _ {\mathrm{t}-2}&=&\sqrt{\alpha_{\mathrm{t}-2}} \mathrm{X} _ {\mathrm{t}-3}+\sqrt{1-\alpha_{\mathrm{t}-2}} \mathrm{Z} _ {\mathrm{t}-3} \\ &...&\\ \quad \mathrm{X} _ {1}&=&\sqrt{\alpha_{1}} \mathrm{X} _ {0}+\sqrt{1-\alpha_{1}} \mathrm{Z} _ {0} \end{array} $$ -
令 $ \bar{\alpha} _ {\mathrm{t}}=\prod_{\mathrm{i}=1}^{\mathrm{t}} \alpha_{\mathrm{i}} $ :
$$ \mathrm{X} _ {\mathrm{t}}=\sqrt{\bar{\alpha} _ {\mathrm{t}}} \mathrm{X} _ {0}+\frac{\sqrt{\bar{\alpha} _ {\mathrm{t}}}}{\sqrt{\alpha_{1}}} \sqrt{1-\alpha_{1}} \mathrm{Z} _ {0}+\frac{\sqrt{\bar{\alpha} _ {\mathrm{t}}}}{\sqrt{\bar{\alpha} _ {2}}} \sqrt{1-\alpha_{2}} \mathrm{Z} _ {1}+\frac{\sqrt{\bar{\alpha} _ {\mathrm{t}}}}{\sqrt{\bar{\alpha} _ {3}}} \sqrt{1-\alpha_{3}} \mathrm{Z} _ {2}+\ldots+\sqrt{1-\alpha_{\mathrm{t}}} \mathrm{Z} _ {\mathrm{t}-1} $$ -
设随机变量 $ \bar{Z} _ {\mathrm{t}-1} $ 为:
$$ \overline{\mathrm{Z}} _ {\mathrm{t}-1}=\frac{\sqrt{\alpha_{\mathrm{t}}}}{\sqrt{\alpha_{1}}} \sqrt{1-\alpha_{1}} \mathrm{Z} _ {0}+\frac{\sqrt{\bar{\alpha} _ {t}}}{\sqrt{\bar{\alpha} _ {2}}} \sqrt{1-\alpha_{2}} \mathrm{Z} _ {1}+\frac{\sqrt{\overline{\alpha_{t}}}}{\sqrt{\alpha_{3}}} \sqrt{1-\alpha_{3}} Z_{2}+\ldots+\sqrt{1-\alpha_{t}} Z_{t-1} $$ -
则 $ \bar{Z} _ {t-1} $ 的期望和方差如下:
$$ \begin{array}{c} \mathrm{E}\left(\overline{\mathrm{Z}} _ {\mathrm{t}-1}\right)=0 \\ \mathrm{D}\left(\overline{\mathrm{Z}} _ {\mathrm{t}-1}\right)=\frac{\bar{\alpha} _ {\mathrm{t}}}{\alpha_{1}}\left(1-\alpha_{1}\right)+\frac{\bar{\alpha} _ {\mathrm{t}}}{\bar{\alpha} _ {2}}\left(1-\alpha_{2}\right)+\frac{\bar{\alpha} _ {\mathrm{t}}}{\bar{\alpha} _ {3}}\left(1-\alpha_{3}\right)+\ldots+\frac{\bar{\alpha} _ {\mathrm{t}}}{\bar{\alpha} _ {\mathrm{t}}}\left(1-\alpha_{\mathrm{t}}\right)=1-\bar{\alpha} _ {\mathrm{t}} \end{array} $$ -
因此有:
$$ \begin{array}{c} \mathrm{X} _ {\mathrm{t}}=\sqrt{\bar{\alpha} _ {\mathrm{t}}} \mathrm{X} _ {0}+\overline{\mathrm{Z}} _ {\mathrm{t}-1}=\sqrt{\bar{\alpha} _ {\mathrm{t}}} \mathrm{X} _ {0}+\sqrt{1-\bar{\alpha} _ {\mathrm{t}}} \mathrm{Z}, \mathrm{Z} \sim \mathrm{N}(0, \mathrm{I}) \\ \mathrm{q}\left(\mathrm{X} _ {\mathrm{t}} \mid \mathrm{X} _ {0}\right)=\mathrm{N}\left(\mathrm{X} _ {\mathrm{t}} ; \sqrt{\bar{\alpha} _ {\mathrm{t}}} \mathrm{X} _ {0},\left(1-\bar{\alpha} _ {\mathrm{t}}\right) \mathrm{I}\right) \end{array} $$ -
至此,我们推出了 $ \mathrm{q}\left(\mathrm{X} _ {\mathrm{t}} \mid \mathrm{X} _ {\mathrm{t}-1}\right) $ 和 $ \mathrm{q}\left(\mathrm{X} _ {\mathrm{t}} \mid \mathrm{X} _ {0}\right) $ 。
逆扩散过程
-
如上图所示,逆扩散过程为从左到右 $X_T \to X_0$ 的过程, 表示从噪声中逐渐复原出图片。
-
如果我们能够在给定$ X_t$ 条件下知道$ X_{t-1}$ 的分布,即如果我们可以知道 $ q(X_{t-1}|X_t)$ ,那我们就能够从任意一张噪声图片中经过一次次的采样得到一张图片而达成图片生成的目的。
-
然而 $ q(X_{t-1}|X_t)$ 很难获得,因此我们需要神经网络学习 $ \operatorname{p_\Theta}\left(\mathrm{X} _ {\mathrm{t}-1} \mid \mathrm{X} _ {\mathrm{t}}\right) $ 来近似 $ \mathrm{q}\left(\mathrm{X} _ {\mathrm{t}-1} \mid \mathrm{X} _ {\mathrm{t}}\right)$。
-
虽然我们不知道 $ q\left(X_{t-1} \mid X_{t}\right) $ ,但是 $ q\left(X_{t-1} \mid X_{t} X_{0}\right) $ 却是可以用 $ q\left(X_{t} \mid X_{0}\right) $ 和 $ q\left(X_{t} \mid X_{t-1}\right) $ 表示的,即 $ q\left(X_{t-1} \mid X_{t} X_{0}\right) $ 是可知的 。
-
因此我们可以用 $ \mathrm{q}\left(\mathrm{X} _ {\mathrm{t}-1} \mid \mathrm{X} _ {\mathrm{t}} \mathrm{X} _ {0}\right) $ 来指导 $ \mathrm{p} \Theta\left(\mathrm{X} _ {\mathrm{t}-1} \mid \mathrm{X} _ {\mathrm{t}}\right) $ 进行训练。
$$ \mathrm{q}\left(\mathrm{X} _ {\mathrm{t}-1} \mid \mathrm{X} _ {\mathrm{t}} \mathrm{X} _ {0}\right)=\frac{\mathrm{q}\left(\mathrm{X} _ {0} \mathrm{X} _ {\mathrm{t}-1} \mathrm{X} _ {\mathrm{t}}\right)}{\mathrm{q}\left(\mathrm{X} _ {0} \mathrm{X} _ {\mathrm{t}}\right)}=\frac{\mathrm{q}\left(\mathrm{X} _ {0} \mathrm{X} _ {\mathrm{t}-1} \mathrm{X} _ {\mathrm{t}}\right)}{\mathrm{q}\left(\mathrm{X} _ {0} \mathrm{X} _ {\mathrm{t}-1}\right)} \frac{\mathrm{q}\left(\mathrm{X} _ {0} \mathrm{X} _ {\mathrm{t}-1}\right)}{\mathrm{q}\left(\mathrm{X} _ {0} \mathrm{X} _ {\mathrm{t}}\right)}=\mathrm{q}\left(\mathrm{X} _ {\mathrm{t}} \mid \mathrm{X} _ {\mathrm{t}-1} \mathrm{X} _ {0}\right) * \frac{\mathrm{q}\left(\mathrm{X} _ {\mathrm{t}-1} \mid \mathrm{X} _ {0}\right)}{\mathrm{q} \left(X_ {\mathrm{t}}|\mathrm{X} _ {0}\right)} $$ -
由于扩散过程是马尔科夫过程:
- 至此,已经把 $ \mathrm{q}\left(\mathrm{X} _ {\mathrm{t}-1} \mid \mathrm{X} _ {\mathrm{t}} \mathrm{X} _ {0}\right) $ 用 $ \mathrm{q}\left(\mathrm{X} _ {\mathrm{t}} \mid \mathrm{X} _ {0}\right) $ 和 $ q\left(\mathrm{X} _ {\mathrm{t}} \mid \mathrm{X} _ {\mathrm{t}-1}\right) $ 进行表示,接下来推导$ \mathrm{q}\left(\mathrm{X} _ {\mathrm{t}-1} \mid \mathrm{X} _ {\mathrm{t}} \mathrm{X} _ {0}\right) $:
-
因为:
$$
\mathrm{X} _ {\mathrm{t}}=\sqrt{\bar{\alpha} _ {\mathrm{t}}} \mathrm{X} _ {0}+\sqrt{1-\bar{\alpha} _ {\mathrm{t}}} \mathrm{Z}, \mathrm{Z} \sim \mathrm{N}(0, \mathrm{I})
$$ -
因此有:
$$ \mathrm{q}\left(\mathrm{X} _ {\mathrm{t}-1} \mid \mathrm{X} _ {\mathrm{t}} \mathrm{X} _ {0}\right)=\mathrm{N}\left(\mathrm{X} _ {\mathrm{t}-1} ; \frac{1}{\sqrt{\alpha_{\mathrm{t}}}} \mathrm{X} _ {\mathrm{t}}-\frac{\beta_{\mathrm{t}}}{\sqrt{\alpha_{\mathrm{t}}\left(1-\bar{\alpha} _ {\mathrm{t}}\right)}} \mathrm{Z}, \frac{1-\bar{\alpha} _ {\mathrm{t}-1}}{1-\bar{\alpha} _ {\mathrm{t}}} \beta_{\mathrm{t}}\right), \mathrm{Z} \sim \mathrm{N}(0, \mathrm{I}) $$ -
至此,得到了 $ \mathrm{q}\left(\mathrm{X} _ {\mathrm{t}-1} \mid \mathrm{X} _ {\mathrm{t}} \mathrm{X} _ {0}\right) $ 的分布表达式。
损失函数
-
我们已经明确了要训练 $ \operatorname{pe}\left(X_{t-1} \mid X_{t}\right) $, 那么目标函数如何确定。
-
有两个很直接的想法:
-
一个是负对数的最大似然概率,即 :$ -\log _ {\mathrm{P} \Theta}\left(\mathrm{X}_ {0}\right) $
-
另一个是真实分布与预测分布的交叉熵,即 :$ -\mathrm{E} _ {\mathrm{q}\left(\mathrm{X} _ {0}\right)} \log \mathrm{p} \Theta\left(\mathrm{X} _ {0}\right) $
-
这两个获取均比较困难,因此参考 VAE, 不去优化这两个东西,而是优化他们的变分上界(variational lower bound)
-
定义 $ L_{V L B} $ 如下:
$$
\mathrm{L} _ {\mathrm{VLB}}=\mathrm{E} _ {\mathrm{q}\left(\mathrm{x} _ {0: \mathrm{T}}\right)}\left[\log \frac{\mathrm{q}\left(\mathrm{X} _ {1: \mathrm{T}} \mid \mathrm{X} _ {0}\right)}{\mathrm{p} _ {\Theta}\left(\mathrm{X} _ {0: \mathrm{T}}\right)}\right]
$$ -
可以证明:
$$ \begin{array}{c} \mathrm{L} _ {\mathrm{VLB}} \geq-\log \mathrm{p} \Theta\left(\mathrm{X} _ {0}\right) \\ \mathrm{~L} _ {\mathrm{VLB}} \geq-\mathrm{E} _ {\mathrm{q}\left(\mathrm{X} _ {0}\right)} \log \mathrm{p} \Theta\left(\mathrm{X} _ {0}\right) \end{array} $$ -
则若减小了 $ L_{V L B} $ 则减小了$ -\log \mathrm{p} \Theta\left(\mathrm{X} _ {0}\right) $ 和 $ -\mathrm{E} _ {\mathrm{q}\left(\mathrm{X} _ {0}\right)} \log \mathrm{p} \Theta\left(\mathrm{X} _ {0}\right) $ 的上界,也就优化了损失函数。
-
$ L_{V L B} $ 定义如下:
$$
\mathrm{L} _ {\mathrm{V} L B}=\mathrm{E} _ {\mathrm{q}\left(\mathrm{x} _ {0: \mathrm{T}}\right)}\left[\log \frac{\mathrm{q}\left(\mathrm{X} _ {1: \mathrm{T}} \mid \mathrm{X} _ {0}\right)}{\mathrm{p \Theta}\left(\mathrm{X} _ {0: \mathrm{T}}\right)}\right]
$$ -
下面证明 $ \mathrm{L} _ {\mathrm{V} \mathrm{LB}} $ 是 $ -\log \mathrm{p} _ {\Theta}\left(\mathrm{X} _ {0}\right) $ 和 $ -\mathrm{E} _ {\mathrm{q}\left(\mathrm{X} _ {0}\right)} \log \mathrm{p} _ {\Theta}\left(\mathrm{X} _ {0}\right) $ 的上界:
-
证明 $ \mathrm{L} _ {\mathrm{V} \mathrm{LB}} \geq-\log \mathrm{P} _ {\Theta}\left(\mathrm{X} _ {0}\right) $ :
$$ \begin{array}{c} -\log \mathrm{p} \Theta\left(\mathrm{X} _ {0}\right) &\leq&-\log \mathrm{p} _ {\Theta}\left(\mathrm{X} _ {0}\right)+\mathrm{D} _ {\mathrm{KL}}\left(\mathrm{q}\left(\mathrm{X} _ {1: \mathrm{t}} \mid \mathrm{X} _ {0}\right)|| \mathrm{p} _ {\Theta}\left(\mathrm{X} _ {1: \mathrm{T}} \mid \mathrm{X} _ {0}\right)\right) \\ &=&-\log \mathrm{p} _ {\Theta}\left(\mathrm{X} _ {0}\right)+\mathrm{E} _ {\mathrm{X} _ {1: \mathrm{T}} \sim \mathrm{q}\left(\mathrm{X} _ {1: \mathrm{T}} \mid \mathrm{X} _ {0}\right)}\left(\log \frac{\mathrm{q}\left(\mathrm{X} _ {1: \mathrm{T}} \mid \mathrm{X} _ {0}\right)}{\mathrm{p} _ {\Theta}\left(\mathrm{X} _ {1: \mathrm{T}} \mid \mathrm{X} _ {0}\right)}\right) \\ &=&-\log _{\Theta}\left(\mathrm{X} _ {0}\right)+\mathrm{E} _ {\mathrm{X} _ {1: \mathrm{T}} \sim \mathrm{q}\left(\mathrm{X} _ {1: \mathrm{T}} \mid \mathrm{X} _ {0}\right)}\left(\log \frac{\mathrm{q}\left(\mathrm{X} _ {1: \mathrm{T}} \mid \mathrm{X} _ {0}\right) \mathrm{p} _ {\Theta}\left(\mathrm{X} _ {0}\right)}{\mathrm{p} _ {\Theta}\left(\mathrm{X} _ {0: \mathrm{T}}\right)}\right) \\ & =&-\log \mathrm{p} _ {\Theta}\left(\mathrm{X} _ {0}\right)+\mathrm{E} _ {\mathrm{X} _ {1: \mathrm{T}} \sim \mathrm{q}\left(\mathrm{X} _ {1: \mathrm{T}} \mid \mathrm{X} _ {0}\right)}\left(\log \frac{\mathrm{q}\left(\mathrm{X} _ {1: \mathrm{T}} \mid \mathrm{X} _ {0}\right)}{\mathrm{p} _ {\Theta}\left(\mathrm{X} _ {0: \mathrm{T}}\right)}+\log \left(\mathrm{p} _ {\Theta}\left(\mathrm{X} _ {0}\right)\right)\right) \\ & =&\mathrm{E} _ {\mathrm{X} _ {0: \mathrm{T}} \sim \mathrm{q}\left(\mathrm{X} _ {0: \mathrm{T}}\right)}\left(\log \frac{\mathrm{q}\left(\mathrm{X} _ {1: \mathrm{T}} \mid \mathrm{X} _ {0}\right)}{\mathrm{p} _ {\Theta}\left(\mathrm{X} _ {0: \mathrm{T}}\right)}\right)=\mathrm{L} _ {\mathrm{VLB}} \end{array} $$ -
证明 $ \mathrm{~L} _ {\mathrm{V} \mathrm{LB}} \geq-\mathrm{E} _ {\mathrm{q}\left(\mathrm{X} _ {0}\right)} \log _{\Theta}\left(\mathrm{X} _ {0}\right) $ :
$$ \begin{array}{c} \mathrm{L} _ {\mathrm{CE}}&=&-\int \mathrm{q}\left(\mathrm{X} _ {0}\right) \log \mathrm{p} _ {\Theta}\left(\mathrm{X} _ {0}\right) \mathrm{dX} _ {0} \\&=&-\mathrm{E} _ {\mathrm{q}\left(\mathrm{X} _ {0}\right)} \log \mathrm{p} _ {\Theta}\left(\mathrm{X} _ {0}\right) \\ &=&-\mathrm{E} _ {\mathrm{q}\left(\mathrm{X} _ {0}\right)} \log \left(\int \mathrm{p} _ {\Theta}\left(\mathrm{X} _ {1: \mathrm{T}} \mid \mathrm{X} _ {0}\right) \mathrm{p} _ {\Theta}\left(\mathrm{X} _ {0}\right) \mathrm{dX} _ {1: \mathrm{T}}\right) \\ &=&-\mathrm{E} _ {\mathrm{q}\left(\mathrm{X} _ {0}\right)} \log \left(\int \mathrm{p} _ {\Theta}\left(\mathrm{X} _ {0: \mathrm{T}}\right) \mathrm{d} \mathrm{X} _ {1: \mathrm{T}}\right) \\ &=&-\mathrm{E} _ {\mathrm{q}\left(\mathrm{X} _ {0}\right)} \log \left(\int \mathrm{q}\left(\mathrm{X} _ {1: \mathrm{T}} \mid \mathrm{X} _ {0}\right) \frac{\mathrm{p} _ {\Theta}\left(\mathrm{X} _ {0: \mathrm{T}}\right)}{\mathrm{q}\left(\mathrm{X} _ {1: \mathrm{T}} \mid \mathrm{X} _ {0}\right)} \mathrm{dX} _ {1: \mathrm{T}}\right) \\ &=&-\mathrm{E} _ {\mathrm{q}\left(\mathrm{X} _ {0}\right)}\left(\log \left(\mathrm{E} _ {\mathrm{q}\left(\mathrm{X} _ {1: \mathrm{T}} \mid \mathrm{X} _ {0}\right)} \frac{\mathrm{p} \Theta\left(\mathrm{X} _ {0: \mathrm{T}}\right)}{\mathrm{q}\left(\mathrm{X} _ {1: \mathrm{T}} \mid \mathrm{X} _ {0}\right)}\right)\right) \\ &\leq&-\mathrm{E} _ {\mathrm{q}\left(\mathrm{X} _ {0}\right)}\left(\mathrm{E} _ {\mathrm{q}\left(\mathrm{X} _ {1: \mathrm{T}} \mid \mathrm{X} _ {0}\right)} \log \left(\frac{\mathrm{P} _ {\Theta}\left(\mathrm{X} _ {0: \mathrm{T}}\right)}{\mathrm{q}\left(\mathrm{X} _ {1: \mathrm{T}} \mid \mathrm{X} _ {0}\right)}\right)\right) \\ &=&\mathrm{E} _ {\mathrm{q}\left(\mathrm{x} _ {0: \mathrm{T}}\right)}\left[\log \frac{\mathrm{q}\left(\mathrm{X} _ {1: \mathrm{T}} \mid \mathrm{X} _ {0}\right)}{\mathrm{p} \Theta\left(\mathrm{X} _ {0: \mathrm{T}}\right)}\right]=\mathrm{L} _ {\mathrm{VLB}} \end{array} $$ -
至此,证明了 $ \mathrm{L} _ {\mathrm{V} \mathrm{LB}} $ 是 $ -\log \mathrm{p} \Theta\left(\mathrm{X} _ {0}\right) $ 和 $ -\mathrm{E} _ {\mathrm{q}\left(\mathrm{X} _ {0}\right)} \log \mathrm{p} \Theta\left(\mathrm{X} _ {0}\right) $ 的上界。
-
简化 $ \mathrm{L} _ {\mathrm{V} \mathrm{LB}} $ :
- $$ \begin{array}{c} \mathrm{L} _ {\mathrm{V} L B}&=& \mathrm{E} _ {\mathrm{q}\left(\mathrm{x} _ {0: \mathrm{T}}\right)}\left[\log \frac{\mathrm{q}\left(\mathrm{X} _ {1: \mathrm{T}} \mid \mathrm{X} _ {0}\right)}{\mathrm{p} _ {\Theta}\left(\mathrm{X} _ {0: \mathrm{T}}\right)}\right] \\ &=&\mathrm{E} _ {\mathrm{q}\left(\mathrm{x} _ {0: \mathrm{T}}\right)}\left[\log \frac{\prod_{\mathrm{t}=1}^{\mathrm{T}} \mathrm{q}\left(\mathrm{X} _ {\mathrm{t}} \mid \mathrm{X} _ {\mathrm{t}-1}\right)}{\mathrm{p}\left(\mathrm{X} _ {\mathrm{T}}\right) \prod_{\mathrm{t}=1}^{\mathrm{T}} \mathrm{P} _ {\Theta}\left(\mathrm{X} _ {\mathrm{t}-1} \mid \mathrm{X} _ {\mathrm{t}}\right)}\right] \\ &=&\mathrm{E} _ {\mathrm{q}\left(\mathrm{x} _ {0: \mathrm{T}}\right)}\left[-\log \mathrm{p} _ {\Theta}\left(\mathrm{X} _ {\mathrm{T}}\right)+\sum_{\mathrm{T}=1}^{\mathrm{T}} \log \frac{\mathrm{q}\left(\mathrm{X} _ {\mathrm{t}} \mid \mathrm{X} _ {\mathrm{t}-1}\right)}{\mathrm{p}\left(\mathrm{X} _ {\mathrm{t}-1} \mid \mathrm{X} _ {\mathrm{t}}\right)}\right] \\ &=&\mathrm{E} _ {\mathrm{q}\left(\mathrm{x} _ {0: \mathrm{T}}\right)}\left[-\log \mathrm{p} _ {\Theta}\left(\mathrm{X} _ {\mathrm{T}}\right)+\sum_{\mathrm{t}=2}^{\mathrm{T}} \log \frac{\mathrm{q}\left(\mathrm{X} _ {\mathrm{t}} \mid \mathrm{X} _ {\mathrm{t}-1}\right)}{\mathrm{p} \Theta\left(\mathrm{X} _ {\mathrm{t}-1} \mid \mathrm{X} _ {\mathrm{t}}\right)}+\log \frac{\mathrm{q}\left(\mathrm{X} _ {1} \mid \mathrm{X} _ {0}\right)}{\left.\mathrm{p} \Theta \mathrm{X} _ {0} \mid \mathrm{X} _ {1}\right)}\right] \\ &=& \mathrm{E} _ {\mathrm{q}\left(\mathrm{X} _ {0: \mathrm{T}}\right)}\left[-\log \mathrm{p} \Theta\left(\mathrm{X} _ {\mathrm{T}}\right)+\sum_{\mathrm{t}=2}^{\mathrm{T}} \log \left(\frac{\mathrm{q}\left(\mathrm{X} _ {\mathrm{t}-1} \mid \mathrm{X} _ {\mathrm{t}} \mathrm{X} _ {0}\right)}{\mathrm{p} _ {\Theta}\left(\mathrm{X} _ {\mathrm{t}-1} \mid \mathrm{X} _ {\mathrm{t}}\right)} * \frac{\mathrm{q}\left(\mathrm{X} _ {\mathrm{t}} \mid \mathrm{X} _ {0}\right)}{\mathrm{q}\left(\mathrm{X} _ {\mathrm{t}-1} \mid \mathrm{X} _ {0}\right)}\right)+\log \frac{\mathrm{q}\left(\mathrm{X} _ {1} \mid \mathrm{X} _ {0}\right)}{\mathrm{p} _ {\Theta}\left(\mathrm{X} _ {0} \mid \mathrm{X} _ {1}\right)}\right] \\ &=&\mathrm{E} _ {\mathrm{q}\left(\mathrm{x} _ {0: \mathrm{T}}\right)}\left[-\log \mathrm{p} _ {\Theta}\left(\mathrm{X} _ {\mathrm{T}}\right)+\sum_{\mathrm{t}=2}^{\mathrm{T}} \log \frac{\mathrm{q}\left(\mathrm{X} _ {\mathrm{t}-1} \mid \mathrm{X} _ {\mathrm{t}} \mathrm{X} _ {0}\right)}{\mathrm{p} _ {\Theta}\left(\mathrm{X} _ {\mathrm{t}-1} \mid \mathrm{X} _ {\mathrm{t}}\right)}+\sum_{\mathrm{t}=2}^{\mathrm{T}} \log \frac{\mathrm{q}\left(\mathrm{X} _ {\mathrm{t}} \mid \mathrm{X} _ {0}\right)}{\mathrm{q}\left(\mathrm{X} _ {\mathrm{t}-1} \mid \mathrm{X} _ {0}\right)}+\log \frac{\mathrm{q}\left(\mathrm{X} _ {1} \mid \mathrm{X} _ {0}\right)}{\mathrm{p} _ {\Theta}\left(\mathrm{X} _ {0} \mid \mathrm{X} _ {1}\right)}\right] \\ &=&\mathrm{E} _ {\mathrm{q}\left(\mathrm{x} _ {0: \mathrm{T}}\right)}\left[-\log \mathrm{p} _ {\Theta}\left(\mathrm{X} _ {\mathrm{T}}\right)+\sum_{\mathrm{t}=2}^{\mathrm{T}} \log \frac{\mathrm{q}\left(\mathrm{X} _ {\mathrm{t}-1} \mid \mathrm{X} _ {\mathrm{t}} \mathrm{X} _ {0}\right)}{\mathrm{p} _ {\Theta}\left(\mathrm{X} _ {\mathrm{t}-1} \mid \mathrm{X} _ {\mathrm{t}}\right)}+\log \frac{\mathrm{q}\left(\mathrm{X} _ {\mathrm{T}} \mid \mathrm{X} _ {0}\right)}{\mathrm{q}\left(\mathrm{X} _ {1} \mid \mathrm{X} _ {0}\right)}+\log \frac{\mathrm{q}\left(\mathrm{X} _ {1} \mid \mathrm{X} _ {0}\right)}{\mathrm{p} \Theta\left(\mathrm{X} _ {0} \mid \mathrm{X} _ {1}\right)}\right] \\ &=&\mathrm{E} _ {\mathrm{q}\left(\mathrm{x} _ {0: \mathrm{T}}\right)}\left[\log \frac{\mathrm{q}\left(\mathrm{X} _ {\mathrm{T}} \mid \mathrm{X} _ {0}\right)}{\mathrm{p} _ {\Theta}\left(\mathrm{X} _ {\mathrm{T}}\right)}+\sum_{\mathrm{t}=2}^{\mathrm{T}} \log \frac{\mathrm{q}\left(\mathrm{X} _ {\mathrm{t}-1} \mid \mathrm{X} _ {\mathrm{t}} \mathrm{X} _ {0}\right)}{\mathrm{p} _ {\Theta}\left(\mathrm{X} _ {\mathrm{t}-1} \mid \mathrm{X} _ {\mathrm{t}}\right)}-\log \mathrm{p} _ {\Theta}\left(\mathrm{X} _ {0} \mid \mathrm{X} _ {1}\right)\right] \\ &=&\mathrm{D} _ {\mathrm{KL}}\left(\mathrm{q}\left(\mathrm{X} _ {\mathrm{T}} \mid \mathrm{X} _ {0}\right) \| \mathrm{p} _ {\Theta}\left(\mathrm{X} _ {\mathrm{T}}\right)\right)+ \sum_{\mathrm{t}=2}^{\mathrm{T}} \mathrm{D} _ {\mathrm{KL}}\left(\mathrm{q}\left(\mathrm{X} _ {\mathrm{t}-1} \mid \mathrm{X} _ {\mathrm{t}} \mathrm{X} _ {0}\right) \| \mathrm{p} _ {\Theta}\left(\mathrm{X} _ {\mathrm{t}-1} \mid \mathrm{X} _ {\mathrm{t}}\right)\right)-\log \mathrm{p} _ {\Theta}\left(\mathrm{X} _ {0} \mid \mathrm{X} _ {1}\right) \\&=&\mathrm{L} _ {\mathrm{T}}+\mathrm{L} _ {\mathrm{T}-1}+\ldots+\mathrm{L} _ {0} \end{array} $$
-
其中:
$$ \begin{array}{c} \mathrm{L} _ {\mathrm{T}}=\mathrm{D} _ {\mathrm{KL}}\left(\mathrm{q}\left(\mathrm{X} _ {\mathrm{T}} \mid \mathrm{X} _ {0}\right) \| \mathrm{p} \Theta\left(\mathrm{X} _ {\mathrm{T}}\right)\right) \\ \mathrm{L} _ {\mathrm{t}}=\mathrm{D} _ {\mathrm{KL}}\left(\mathrm{q}\left(\mathrm{X} _ {\mathrm{t}} \mid \mathrm{X} _ {\mathrm{t}}+1 \mathrm{X} _ {0}\right) \| \mathrm{p} \Theta\left(\mathrm{X} _ {\mathrm{t}} \mid \mathrm{X} _ {\mathrm{t}+1}\right)\right), 1 \leq \mathrm{t} \leq \mathrm{T} \\ \mathrm{L} _ {0}=-\log \mathrm{p} \Theta\left(\mathrm{X} _ {0} \mid \mathrm{X} _ {1}\right) \end{array} $$ -
从 $ \mathrm{L} _ {\mathrm{t}} $ 即可看出,对 $ \mathrm{p} _ {\Theta}\left(\mathrm{X} _ {\mathrm{t}} \mid \mathrm{X} _ {\mathrm{t}+1}\right) $ 的监督就是最小化 $ \mathrm{p} _ {\Theta}\left(\mathrm{X} _ {\mathrm{t}} \mid \mathrm{X} _ {\mathrm{t}+1}\right) $ 和 $ \mathrm{q}\left(\mathrm{X} _ {\mathrm{t}} \mid \mathrm{X} _ {\mathrm{t}+1} \mathrm{X} _ {0}\right) $ 的KL散度。
参考资料
- 《Denoising Diffusion Probabilistic Models》
- 《Diffusion Models Beat GANs on Image Synthesis》
- https://zhuanlan.zhihu.com/p/532736667
- https://zhuanlan.zhihu.com/p/529525303
- https://blog.csdn.net/weixin_44846680/article/details/117414296
- https://blog.csdn.net/Little_White_9/article/details/124435560
- https://lilianweng.github.io/posts/2021-07-11-diffusion-models/#forward-diffusion-process
- http://www.pczh.cn/news/27360.html
- https://lilianweng.github.io/posts/2021-07-11-diffusion-models/
- https://yinglinzheng.netlify.app/diffusion-model-tutorial/
文章链接:
https://www.zywvvd.com/notes/study/deep-learning/generation/diffusion-model/diffusion-model/
“觉得不错的话,给点打赏吧 ୧(๑•̀⌄•́๑)૭”

微信支付

支付宝支付