Memory Bank

异常检测是无监督任务的重要应用，本文记录一个重要的相关技巧 Memory Bank。

基于重构的异常检测

• 异常检测重要一脉是基于重构的方法，常见的方法是基于 Auto-Encoder ，对输入数据进行重构

• 根据重构误差判断是否有异常部分

Memory Bank (trained)

• 在基于重构的视频异常检测任务中用到了 Memory Bank

  Memorizing Normality to Detect Anomaly: Memory-augmented Deep Autoencoder for Unsupervised Anomaly Detection (2019 CVPR)

• 流程框架

  

• MemAE 的整体结构框架主要分为三个部分：Encoder/ Memory module/ Decoder

Encoder / Decoder : U-net 结构

• 假设 Encoder 生成的 feature maps 大小为 $(H,W,C)$，则将其拆分成 $H\ast W$ 个 $(1,1,C)$ 的 queries 作为 Memory module 模块的输入，所以 Encoder 可以视为是 query 生成器；Decoder输入是 Memory module 生成的大小为 $(H,W,C)$ 的新的 feature maps，用来重构生成图片。

  $$\begin{array}{l}z=f_c(x;{\theta }_c)\\ x^{\prime }=f_d(z^{\prime };{\theta }_d)\end{array}$$

• 上式中，${\theta }_e,{\theta }_d$ 分别为Encoder / Decoder模型参数，$x$ 为输入图片，$z$ 为Encoder生成的feature maps，$z^{\prime }$ 为Memory module生成的新feature maps，$x^{\prime }$ 为重构生成的图片。

Memory module

• 如图架构所示，Memory items: M.shape=$(N,C)$，$C$ 与 Encoder feature maps 相同，$N$ 为 Memory items个数，超参数，根据需要调整，论文最后消融实验证明模型性能与 $N$ 关系不大，具体参加论文实验部分，图中 Memory Addressing 计算每一个 query 与所有Memory items 的权重 $w$：

$$w_i=\frac{exp(d(z,m_i))}{\sum _{j=1}^{N}exp(d(z,m_j))}$$

$$d(z,m_i)=\frac{z{m}_i^T}{|||z|||m_i||}$$

• 上面提到过因为卷积网络的泛华性能过强会导致异常帧重构后也会得到较小的重构误差，这里为了避免发生这类问题，对计算出来的相似度权重进行了类似 RELU 操作，即相似度权重小于某阈值时清零：

$$w_i^{\prime }=\frac{max(w_i-X_j)\cdot w_i}{|w_i-X||+e}$$

• 基于以上步骤，Memory module 产生新的 feature maps：

$$z=WM=\sum _{i=1}^N{w}_i{m}_i$$

• 以上即为Memory module部分的计算步骤，可以理解为对Encoder feature maps的重构，生成的新feature maps包含了更多关于正常帧的信息，使得Decoder重构之后异常帧能够得到较大的重构误差。

目标函数

• 重构任务自然是要有重构误差指标，所以目标函数第一项就是最小化重构误差：

$$R(x^t,x^{\prime t})=||x^t-x^{\prime t}|{|}_2^2$$

• 上面提到为了避免异常帧重构得到较小重构误差的问题，设定阈值 $\lambda$ 对较小相似度权重 $w$ 清零，所以目标函数第二项就是为了保证相似度权重 $w^{\prime }$ 尽可能的稀疏，通过最小化$w^{\prime }$ 的熵来实现，即：

$$E(w^{\prime t})=\sum _{i=1}^T-w_i\cdot \log (w_i)$$

• 综上，MemAE最终的目标函数为：

$$L({\theta }_c,{\theta }_d,M)=\frac{1}{T}\sum _{t=1}^{T}R(x^t,x^{\prime t})+\alpha E(w^{\prime t}))$$

小结

在Encoder / Decoder中加入Memory module帮助增强模型记忆正常帧信息的能力，将其插入在Encoder之后，Decoder之前，处理生成的feature maps，Memory items需要优先进行初始化，并通过网络的反向传播来进行更新，Memory items是整个网络权重的一部分，也因为这个原因，Memory items只能在训练过程中进行迭代优化，测试过程中是不改变的。论文对各项超参数的选取及目标函数的选取都进行了消融实验，实验详情见论文第四部分。

Memory Bank (independent)

• Learning Memory-guided Normality for Anomaly Detection (2020 CVPR) 用到了类似的结构，不过 Memory Bank 是独立于网络的

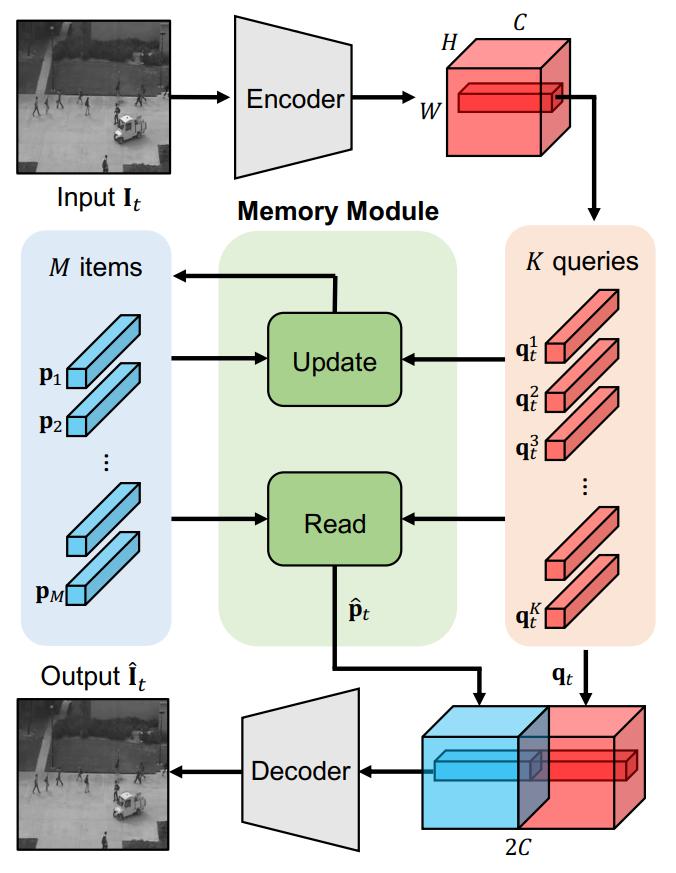
• 也是分为三个部分: Encoder / Memory Module / Decoder。区别主要有两点，第一是Memory Module的计算过程，第二是Decoder的输入是Memory Module feature maps + Encoder feature maps。这里重点讲 Memory Module。
• 在2019年论文中Memory items是通过梯度回传进行迭代更新的，所以不能再测试阶段进行改变，在这篇论文中，将Memory Module作为了一个独立于整体网络参数之外的一个部分，不通过梯度回传进行更新，而是通过作者指定的方式进行更新，所以，只要判断输入为正常帧时就对Memory items进行更新，训练测试阶段都可进行，使得模型具有了一定适应新场景的能力。作为独立于整体模型参数之外的部分，其主要分为两部分：Update / Read

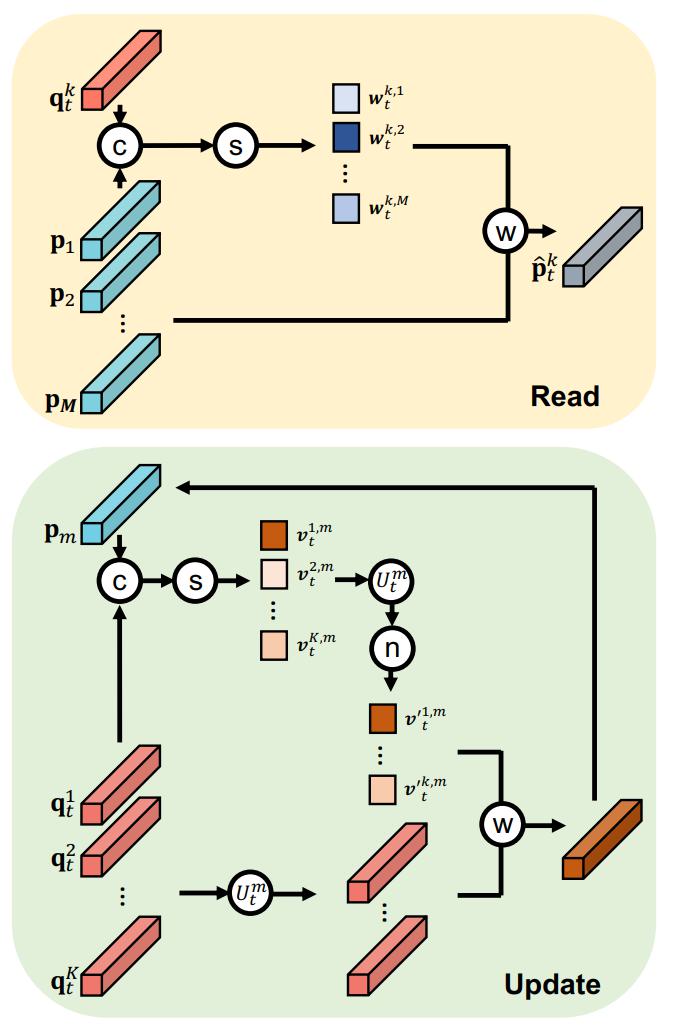
Read

• 用来生成新的feature maps

• 这里的计算方法和2019年论文基本相似，其文字叙述过程可以概括为：每一个query和所有Memory items计算余弦相似度，相似度与对应的Memory item相乘之后相加求和得到新的feature maps：

  $$w_t^{k,m}=\frac{\exp \left({\left(p_m\right)}^T{q}_t^k\right)}{\sum _{\tilde{m}=1}^M\exp \left({\left(p_{\tilde{m}}\right)}^T{q}_t^k\right)}$$

• 新 feature maps 计算：

  $${\tilde{p}}_t^k=\sum _{\tilde{m}=1}^M{w}_t^{k,\tilde{m}}{p}_{\tilde{m}}$$

Update

• 这里的Update更新Memory items是在原先基础上加上改变量实现的：

  $$p^m\leftarrow f(p^m+\sum _{k\in U_t^m}{\tilde{v}}_t^{k,m}{q}_t^k)$$

• 文字叙述其过程可以概括为：每一个Memory item与所有queries计算余弦相似度，相似度进行normalize，与对应的query相乘然后求和得到改变量，将改变量与原始Memory item相加得到更新之后的Memory items。

• 余弦相似度计算：

  $$v_t^{k,m}=\frac{\exp \left({\left(p_m\right)}^T{q}_t^k\right)}{\sum _{\tilde{k}}^K\exp \left({\left(p_m\right)}^T{q}_t^{\tilde{k}}\right)}$$

• 归一化：

  $${\tilde{v}}_t^{k,m}=\frac{v_t^{k,m}}{\underset{\tilde{k}\in U_t^m}{max}{v}_t^{\tilde{k},m}}$$

• 更新触发条件为输入帧为正常帧，在训练阶段都是正常帧，每一步都进行更新，但是在测试时，不知道输入是否为正常帧，所以为了判断，论文引入了一个新的变量 ${\epsilon }_t$ (regular score)判断当前帧是否为正常帧：

  $${\epsilon }_t=\sum _{i,j}{W}_{ij}({\tilde{I}}_t,I_t){\Vert {\tilde{I}}_t^{ij}-I_t^{ij}\Vert }_2$$ $$W_{ij}({\tilde{I}}_t,I_t)=\frac{1-\exp (-{\Vert {\tilde{I}}_t^{ij}-I_t^{ij}\Vert }_2)}{\sum _{i,j}1-\exp (-{\Vert {\tilde{I}}_t^{ij}-I_t^{ij}\Vert }_2)}$$

目标函数

• 这里的目标函数分为三部分：重构损失(reconstruction loss)、特征紧密度损失(feature compactness loss)、特征分散度损失(feature separateness loss)

$$L=L_{rec}+{\lambda }_c{L}_{\text{compact }}+{\lambda }_s{L}_{\text{separate }}$$

重构损失(reconstruction loss)：

$$L_{rec}=\sum _t^T{\Vert {\tilde{I}}_t-I_t\Vert }^2$$

重构损失旨在使模型输出尽可能接近输入，记录正常模式信息，使得输入为异常帧时得到较大的重构误差，区分正常/异常帧。

特征紧密度损失(feature compactness loss)：

$$L_{\text{compact }}=\sum _t^T\sum _k^K{\Vert q_t^k-p_p\Vert }_2$$ $$p={\mathrm{argmax}}_{m\in M}{w}_t^{k,m}$$

• 特征紧密损失的主体思想是：使得 Memory item 与离它最接近的query尽可能的靠近， $p$ 代表了最靠近当前 query 的 Memory item

每一个五角星代表一个Memory item，该损失的作用类似于聚类，使得每个类别(正常帧特征) 尽可能的接近聚类中心(Memory items)

特征分散度损失(feature separateness loss)：

$$L_{\text{separate }}=\sum _t^T\sum _k^K{[{\Vert q_t^k-p_p\Vert }_2-{\Vert q_t^k-p_n\Vert }_2+\alpha ]}_{+}$$ $$n=\mathrm{argmax}{x}_{m\in M,m\ne p}{w}_t^{k,m}$$

• 在紧密度损失中，使得同类别的query尽可能的接近对应的Memory items，但是可能会导致一个问题：Memory item之间的距离过近，没有区分度，为了避免这个问题，在目标函数中添加了一项分散度损失，损失的第一项和紧密度损失一直，第二项表示离对应Memory item第二接近的query要尽可能的远离当前Memory item，确保不同Memory item之间具有区分性。如图6所示，这项损失使得不同Memory item(五角星)之间可分。

论文小结

• Memory Module仍然是插入在Encoder / Decoder之间。和第一篇论文相似，需要初始化Memory Module，区别在于不通过网络权重反向传播更新，并且在训练和测试时均可更新，前提是要判断当前帧是否正常，这里判断正常帧的方法不够准确，但是通过实验发现确实能够帮助提升精度。论文同样对目标函数及各项超参数进行了消融实验，具体实验步骤及结果见论文第四部分。

参考资料

• https://zhuanlan.zhihu.com/p/404715378
• Memorizing Normality to Detect Anomaly: Memory-augmented Deep Autoencoder for Unsupervised Anomaly Detection (2019 CVPR)
• Learning Memory-guided Normality for Anomaly Detection (2020 CVPR)
• Learning Normal Dynamics in Videos with Meta Prototype Network (2021 CVPR)

文章链接：
https://www.zywvvd.com/notes/study/deep-learning/block/memory-bank/memory-bank/