本文最后更新于:2024年5月7日 下午
卡尔曼滤波是非常经典的预测追踪算法,能够在系统存在噪声和干扰的情况下进行系统状态的最优估计,广泛使用在导航、制导、控制相关的领域。
简介
- SLAM 过程可以由运动方程和观测方程来描述,考虑一个简单的场景,在离散的时间 $t=0…N$ 的时间内,有一个机器人“小萝卜”,他在这些时间上不断控制自己做着各种各样的动作,每个对应时刻有自己的状态变量 $[x_0, …, x_N]$,在过程中也会产生某种观测变量 $[y_0, …,y_N]$
- 在实际数据产生过程中,必定会带有误差,控制系统会有控制误差,观测会产生测量误差,如果误差符合某种分布,那么状态和观测值也是服从某种概率分布的随机变量。
- 因此,我们关心的问题就变成:当我们拥有某些运动数据和观测数据之时,如何确定状态量 $x,y$ 的分布。
问题描述
- 考虑在 $k$ 时刻下,“小萝卜” 的状态随机变量用 $x_k$ 表示,这个时刻控制变量用 $u_k$ 表示,控制噪声用 $w_k$ 表示,此时观测到的数据记作 $z_k$,观测噪声为 $v_k$,于是可以写出运动与观测方程:
$$
\left\{\begin{array}{l}\boldsymbol{x}_{k}=f\left(\boldsymbol{x}_{k-1}, \boldsymbol{u}_{k}\right)+\boldsymbol{w}_{k} \\ \boldsymbol{z}_{k}=h\left(\boldsymbol{x}_{k}\right)+\boldsymbol{v}_{k}\end{array} \quad k=1, \ldots, N\right.
$$
- 我们希望用过去 $0$ 到 $k$ 中的数据来估计现在的状态分布:
$$
P\left(\boldsymbol{x}_{k} \mid \boldsymbol{x}_{0}, \boldsymbol{u}_{1: k}, \boldsymbol{z}_{1: k}\right)
$$
- 当我们只关注 $x_k$ 与 $z_k$ 时,根据贝叶斯法则:
$$
\begin{array}{c}
P\left(\boldsymbol{x}_{k},z_k \mid \boldsymbol{x}_{0}, \boldsymbol{u}_{1: k}, \boldsymbol{z}_{1: k-1}\right) =P\left(\boldsymbol{x}_{k} \mid \boldsymbol{x}_{0}, \boldsymbol{u}_{1: k}, \boldsymbol{z}_{1: k}\right)·P(z_k)\\
= P\left(\boldsymbol{z}_{k} \mid \boldsymbol{x}_{k}\right) P\left(\boldsymbol{x}_{k} \mid \boldsymbol{x}_{0}, \boldsymbol{u}_{1: k}, \boldsymbol{z}_{1: k-1}\right)
\end{array}
$$
$$
P\left(\boldsymbol{x}_{k} \mid \boldsymbol{x}_{0}, \boldsymbol{u}_{1: k}, \boldsymbol{z}_{1: k}\right) \propto P\left(\boldsymbol{z}_{k} \mid \boldsymbol{x}_{k}\right) P\left(\boldsymbol{x}_{k} \mid \boldsymbol{x}_{0}, \boldsymbol{u}_{1: k}, \boldsymbol{z}_{1: k-1}\right)
$$
- 右边第一项为似然,第二项为先验。
- 还有一个假设是 $x_k$ 是基于过去所有的状态估计得到的,那么 $x_k$ 至少会受到 $x_{k-1}$ 的影响,那么以 $ \boldsymbol{x}_{k-1} $ 时刻为条件概率展开:
$$
P\left(\boldsymbol{x}_{k} \mid \boldsymbol{x}_{0}, \boldsymbol{u}_{1: k}, \boldsymbol{z}_{1: k-1}\right)=\int P\left(\boldsymbol{x}_{k} \mid \boldsymbol{x}_{k-1}, \boldsymbol{x}_{0}, \boldsymbol{u}_{1: k}, \boldsymbol{z}_{1: k-1}\right) P\left(\boldsymbol{x}_{k-1} \mid \boldsymbol{x}_{0}, \boldsymbol{u}_{1: k}, \boldsymbol{z}_{1: k-1}\right) \mathrm{d} \boldsymbol{x}_{k-1}
$$
滤波器模型
- 我们假设这个状态变化具有马尔科夫性,也就是 $k$ 时刻的状态仅与 ${k-1}$ 时刻状态有关,上述积分式的右边第一项:
$$
P\left(\boldsymbol{x}_{k} \mid \boldsymbol{x}_{k-1}, \boldsymbol{x}_{0}, \boldsymbol{u}_{1: k}, \boldsymbol{z}_{1: k-1}\right)=P\left(\boldsymbol{x}_{k} \mid \boldsymbol{x}_{k-1}, \boldsymbol{u}_{k}\right)
$$
$$
P\left(\boldsymbol{x}_{k-1} \mid \boldsymbol{x}_{0}, \boldsymbol{u}_{1: k}, \boldsymbol{z}_{1: k-1}\right)=P\left(\boldsymbol{x}_{k-1} \mid \boldsymbol{x}_{0}, \boldsymbol{u}_{1: k-1}, \boldsymbol{z}_{1: k-1}\right)
$$
线性高斯系统
- 我们从形式最简单的线性高斯系统开始,最后得到卡尔曼滤波器。明确了起点和终点之后,我们再来考虑中间的路线。线性高斯系统是指,运动方程和观测方程可以由线性方程来描述:
$$
\left\{\begin{array}{l}\boldsymbol{x}_{k}=\boldsymbol{A}_{k} \boldsymbol{x}_{k-1}+\boldsymbol{u}_{k}+\boldsymbol{w}_{k} \\ \boldsymbol{z}_{k}=\boldsymbol{C}_{k} \boldsymbol{x}_{k}+\boldsymbol{v}_{k}\end{array} \quad k=1, \ldots, N\right.
$$
$$
\boldsymbol{w}_{k} \sim N(\mathbf{0}, \boldsymbol{R}) . \quad \boldsymbol{v}_{k} \sim N(\mathbf{0}, \boldsymbol{Q})
$$
- 利用马尔科夫性,假设我们知道了在 $k-1$ 时刻的后验(在 $ k-1 $ 时刻看来) 状态估计 $ \hat{\boldsymbol{x}}_{k-1} $ 及其协方差 $ \hat{\boldsymbol{P}}_{k-1} $, 现在要根据 $ k $ 时刻的输人和观 测数据, 确定 $ \boldsymbol{x}_{k} $ 的后验分布。
- 为区分推导中的先验和后验, 我们在记号上做一点区别:以上帽子 $ \hat{\boldsymbol{x}}_{k} $ 表示后验, 以下帽子 $ \check{\boldsymbol{x}}_{k} $ 表示先验分布。
卡尔曼滤波
预测
- 卡尔曼滤波器的第一步为预测, 通过运动方程确定 $ \boldsymbol{x}_{k} $ 的先验分布。这一步是线性的,而高斯分布的线性变换仍是高斯分布。
- 而且协方差矩阵具有性质:
$$
\begin{aligned} \operatorname{Cov}(x) & =\Sigma \\ \operatorname{Cov}(\mathbf{A} x) & =\mathbf{A} \Sigma \mathbf{A}^{T}\end{aligned}
$$
$$
P\left(\boldsymbol{x}_{k} \mid \boldsymbol{x}_{0}, \boldsymbol{u}_{1: k}, \boldsymbol{z}_{1: k-1}\right)=N\left(\boldsymbol{A}_{k} \hat{\boldsymbol{x}}_{k-1}+\boldsymbol{u}_{k}, \boldsymbol{A}_{k} \hat{\boldsymbol{P}}_{k-1} \boldsymbol{A}_{k}^{\mathrm{T}}+\boldsymbol{R}\right)
$$
- 它显示了如何从上一个时刻的状态,根据输入信息(但是有噪声)推断当前时刻的状态分布。这个分布也就是
先验。
$$
\check{\boldsymbol{x}}_{k}=\boldsymbol{A}_{k} \hat{\boldsymbol{x}}_{k-1}+\boldsymbol{u}_{k}, \quad \check{\boldsymbol{P}}_{k}=\boldsymbol{A}_{k} \hat{\boldsymbol{P}}_{k-1} \boldsymbol{A}_{k}^{\mathrm{T}}+\boldsymbol{R}
$$
- 显然这一步状态的不确定度要变大,因为系统中添加了噪声。
观测
- 由观测方程,我们可以计算在某个状态下应该产生怎样的观测数据,可以认为这就是
似然:
$$
P\left(\boldsymbol{z}_{k} \mid \boldsymbol{x}_{k}\right)=N\left(\boldsymbol{C}_{k} \boldsymbol{x}_{k}, \boldsymbol{Q}\right)
$$
$$
\boldsymbol{x}_{k} \sim N\left(\hat{\boldsymbol{x}}_{k}, \hat{\boldsymbol{P}}_{k}\right)
$$
- 根据上文的贝叶斯公式,这个
似然与先验乘积与后验相差一个常数倍
$$
N\left(\hat{\boldsymbol{x}}_{k}, \hat{\boldsymbol{P}}_{k}\right)=\eta N\left(\boldsymbol{C}_{k} \boldsymbol{x}_{k}, \boldsymbol{Q}\right) \cdot N\left(\check{\boldsymbol{x}}_{k}, \check{\boldsymbol{P}}_{k}\right)
$$
- 这里我们稍微用点讨巧的方法。既然我们已经知道等式两侧都是高斯分布,那就只需比较指数部分,无须理会高斯分布前面的因子部分。指数部分很像是一个二次型的配方,我们来推导一下。首先把指数部分展开,有:
$$
\left(\boldsymbol{x}_{k}-\hat{\boldsymbol{x}}_{k}\right)^{\mathrm{T}} \hat{\boldsymbol{P}}_{k}^{-1}\left(\boldsymbol{x}_{k}-\hat{\boldsymbol{x}}_{k}\right)=\left(\boldsymbol{z}_{k}-\boldsymbol{C}_{k} \boldsymbol{x}_{k}\right)^{\mathrm{T}} \boldsymbol{Q}^{-1}\left(\boldsymbol{z}_{k}-\boldsymbol{C}_{k} \boldsymbol{x}_{k}\right)+\left(\boldsymbol{x}_{k}-\check{\boldsymbol{x}}_{k}\right)^{\mathrm{T}} \check{\boldsymbol{P}}_{k}^{-1}\left(\boldsymbol{x}_{k}-\check{\boldsymbol{x}}_{k}\right)
$$
- 为了求左侧的 $ \hat{\boldsymbol{x}}_{k} $ 和 $ \hat{\boldsymbol{P}}_{k} $ , 我们把两边展开, 并比较 $ \boldsymbol{x}_{k} $ 的二次和一次系数。对于二次系数, 有:
$$
\hat{\boldsymbol{P}}_{k}^{-1}=\boldsymbol{C}_{k}^{\mathrm{T}} \boldsymbol{Q}^{-1} \boldsymbol{C}_{k}+\check{\boldsymbol{P}}_{k}^{-1}
$$
- 该式给出了协方差的计算过程。为了便于后面列写式子, 定义一个中间变量:
$$
\boldsymbol{K}=\hat{\boldsymbol{P}}_{k} \boldsymbol{C}_{k}^{\mathrm{T}} \boldsymbol{Q}^{-1}
$$
- 左右各乘 $ \hat{\boldsymbol{P}}_{k} $, 有:
$$
\boldsymbol{I}=\hat{\boldsymbol{P}}_{k} \boldsymbol{C}_{k}^{\mathrm{T}} \boldsymbol{Q}^{-1} \boldsymbol{C}_{k}+\hat{\boldsymbol{P}}_{k} \check{\boldsymbol{P}}_{k}^{-1}=\boldsymbol{K} \boldsymbol{C}_{k}+\hat{\boldsymbol{P}}_{k} \check{\boldsymbol{P}}_{k}^{-1}
$$
$$
\hat{\boldsymbol{P}}_{k}=\left(\boldsymbol{I}-\boldsymbol{K} \boldsymbol{C}_{k}\right) \check{\boldsymbol{P}}_{k}
$$
$$
\begin{aligned}
-2 \hat{\boldsymbol{x}}_{k}^{\mathrm{T}} \hat{\boldsymbol{P}}_{k}^{-1} \boldsymbol{x}_{k}&=-2 \boldsymbol{z}_{k}^{\mathrm{T}} \boldsymbol{Q}^{-1} \boldsymbol{C}_{k} \boldsymbol{x}_{k}-2 \check{\boldsymbol{x}}_{k}^{\mathrm{T}} \check{\boldsymbol{P}}_{k}^{-1} \boldsymbol{x}_{k} \\
\hat{\boldsymbol{P}}_{k}^{-1} \hat{\boldsymbol{x}}_{k}&=\boldsymbol{C}_{k}^{\mathrm{T}} \boldsymbol{Q}^{-1} \boldsymbol{z}_{k}+\check{\boldsymbol{P}}_{k}^{-1} \check{\boldsymbol{x}}_{k} \\
\hat{\boldsymbol{x}}_{k} & =\hat{\boldsymbol{P}}_{k} \boldsymbol{C}_{k}^{\mathrm{T}} \boldsymbol{Q}^{-1} \boldsymbol{z}_{k}+\hat{\boldsymbol{P}}_{k} \check{\boldsymbol{P}}_{k}^{-1} \check{\boldsymbol{x}}_{k} \\ \hat{\boldsymbol{x}}_{k}&=\boldsymbol{K} \boldsymbol{z}_{k}+\left(\boldsymbol{I}-\boldsymbol{K} \boldsymbol{C}_{k}\right)\check{\boldsymbol{x}}_{k} \\
\hat{\boldsymbol{x}}_{k}&=\check{\boldsymbol{x}}_{k}+\boldsymbol{K}\left(\boldsymbol{z}_{k}-\boldsymbol{C}_{k} \check{\boldsymbol{x}}_{k}\right)\end{aligned}
$$
- 于是我们又得到了后验均值的表达。总而言之,上面的两个步骤可以归纳为
预测和更新(Update)两个步骤:
-
预测:
$$
\check{\boldsymbol{x}}_{k}=\boldsymbol{A}_{k} \hat{\boldsymbol{x}}_{k-1}+\boldsymbol{u}_{k}, \quad \check{\boldsymbol{P}}_{k}=\boldsymbol{A}_{k} \hat{\boldsymbol{P}}_{k-1} \boldsymbol{A}_{k}^{\mathrm{T}}+\boldsymbol{R}
$$
-
更新:先计算 $ \boldsymbol{K} $, 它又称为卡尔曼增益:
$$
\boldsymbol{K}=\check{\boldsymbol{P}}_{k} \boldsymbol{C}_{k}^{\mathrm{T}}\left(\boldsymbol{C}_{k} \check{\boldsymbol{P}}_{k} \boldsymbol{C}_{k}^{\mathrm{T}}+\boldsymbol{Q}_{k}\right)^{-1}
$$
-
计算后验概率的分布:
$$
\begin{array}{l}\hat{\boldsymbol{x}}_{k}=\check{\boldsymbol{x}}_{k}+\boldsymbol{K}\left(\boldsymbol{z}_{k}-\boldsymbol{C}_{k} \check{\boldsymbol{x}}_{k}\right) \\ \hat{\boldsymbol{P}}_{k}=\left(\boldsymbol{I}-\boldsymbol{K} \boldsymbol{C}_{k}\right) \check{\boldsymbol{P}}_{k}\end{array}
$$
实现代码
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
| import numpy as np
import matplotlib.pyplot as plt
import matplotlib.animation as animation
import cv2
def target_simple(t):
x_t = 100
y_t = 100 + t
return x_t, y_t
def get_u(target_xy, cur_xy, length):
d_v = np.mat(target_xy).T - cur_xy
mode_d = (np.array(d_v) ** 2).sum() ** 0.5
u = d_v / mode_d * length
return u
d_t = 1
data_init = np.mat([[0], [0], [0], [0]])
P_init = np.zeros([4, 4])
A = np.mat([
[1, 0, d_t, 0],
[0, 1, 0, d_t],
[0, 0, 1, 0],
[0, 0, 0, 1]
])
B = np.mat([
[0.5 * d_t * d_t, 0],
[0, 0.5 * d_t * d_t],
[d_t, 0],
[0, d_t]
])
sigma_r = 0.0
R = np.mat(np.eye(4) * (1 - sigma_r) + sigma_r) * 0.1
C = np.eye(4)
sigma_q = 0.0
Q = np.mat(np.eye(4) * (1 - sigma_q) + sigma_q) * 0.1
u_l = 1
data_list = [data_init]
P_list = [P_init]
target_pos_list = [target_simple(0)]
fig, ax = plt.subplots(1, 1)
plt.grid(ls='--')
ax.set_xlim(-100, 500)
ax.set_ylim(-100, 800)
line_missile, = plt.plot(data_list[0][0],data_list[0][1], 'r-')
line_fly, = plt.plot(target_pos_list[0][0],target_pos_list[0][1], 'b-')
label_data = 200
def fly_update(index):
x_t, y_t = target_simple(index)
target_pos_list.append(target_simple(index))
cur_u = get_u([x_t, y_t], data_list[index - 1][:2], u_l)
x_pre = A * data_list[index - 1] + B * cur_u
p_pre = A * P_list[index - 1] * A.T + R
control_noise = np.mat(np.random.multivariate_normal([0, 0, 0, 0], R, 1).T)
real_x = x_pre + control_noise
view_noise = np.mat(np.random.multivariate_normal([0, 0, 0, 0], Q, 1).T)
z_k = C * real_x + view_noise
K = (p_pre * C) * ((C * p_pre * C.T + Q) ** -1)
x_post = x_pre + K * (z_k - C * x_pre)
P_post = (np.mat(np.eye(4))- K * C) * p_pre
data_list.append(x_post)
P_list.append(P_post)
pos_data = np.array(data_list)[:, :2, 0]
fly_data = np.array(target_pos_list)[:, :2]
line_missile, = plt.plot(pos_data[:, 0],pos_data[:, 1], 'r-')
line_fly, = plt.plot(fly_data[:, 0],fly_data[:, 1], 'b-')
return line_missile, line_fly,
def fly_init():
pos_data = np.array(data_list)[:, :2, 0]
line_missile.set_data(pos_data[:, 0], pos_data[:, 1])
fly_data = np.array(target_pos_list)[:, :2]
line_fly, = plt.plot(fly_data[:, 0],fly_data[:, 1], 'b-')
return line_missile, line_fly,
fly_anim = animation.FuncAnimation(fig=fig, func=fly_update,
frames=np.arange(1, label_data),
init_func=fly_init, interval=100, blit=True)
fly_anim.save('vvd_missile.gif', writer='pillow', fps=10)
plt.show()
|
-
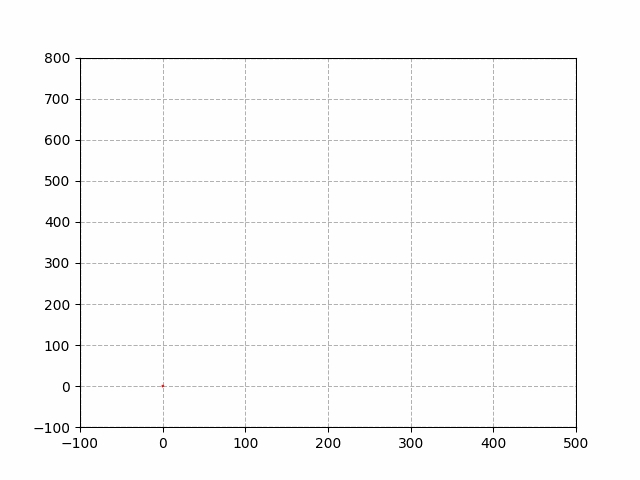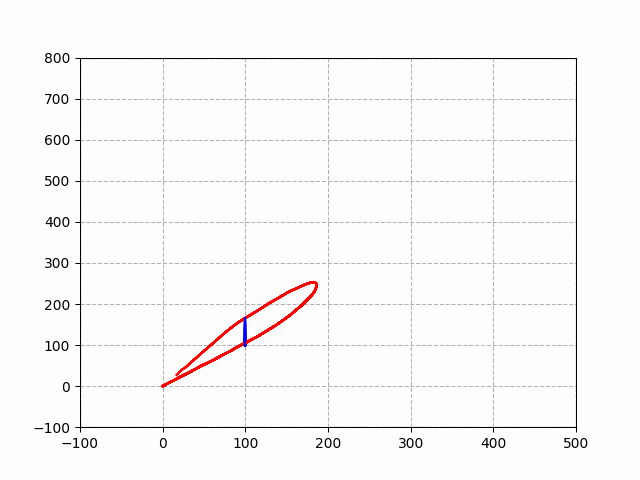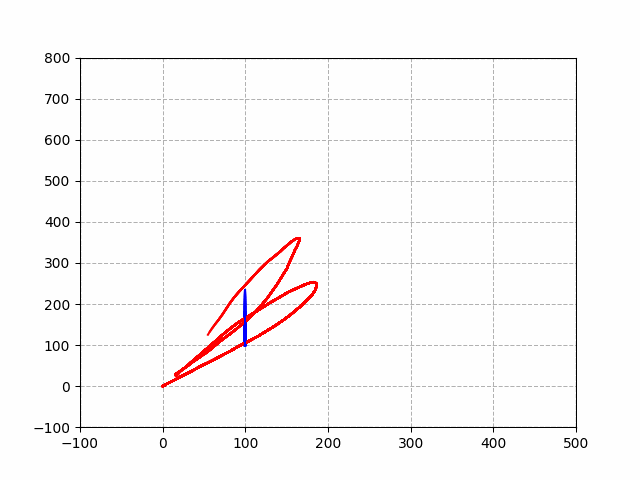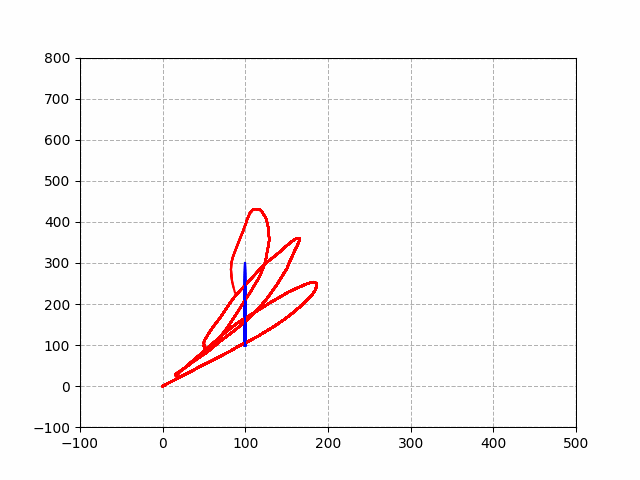
实现效果:
对,控制的方法并不科学,应该是打不着飞机了,提供一个可供参考的实现过程
参考资料
文章链接:
https://www.zywvvd.com/notes/study/SLAM/kalman-filter/kalman-filter/


