概率论基础 - 5 - 马尔可夫不等式

马尔可夫不等式把概率关联到数学期望，给出了随机变量的累积分布函数一个宽泛但仍有用的界。

定义

马尔可夫不等式用于估计尾事件的概率上界。

• 若随机变量$X$只取非负值，则$\forall a>0$有：

$$
\mathbb{P}(X \geq a) \leq \frac{\mathbb{E}(X)}{a}
$$

证明

思路1

放大概率，得到部分函数期望

截断函数期望，二者相比较

• 考虑 $X\ge a$的情况 → $\frac {X}{a} \ge 1$
• 对于不等式左边有：

$$
\mathbb P(X \geq a)=\int_{a}^{+\infty} f(x) d x \leq \int_{a}^{+\infty} \frac{X}{a} f(x) d x
$$

• 对于不等式右边有：

$$
E\left(\frac{X}{a}\right)=\int_{-\infty}^{a} \frac{X}{a} f(x) d x+\int_{a}^{+\infty} \frac{X}{a} f(x) d x
$$

• 由于：

$$
\int_{-\infty}^{a} \frac{X}{a} f(x) d x \geq 0
$$

• 因此：

$$
\mathbb P(X \geq a) \leq \int_{a}^{+\infty} \frac{X}{a} f(x) d x \leq E\left(\frac{X}{a}\right)
$$

• 即：

$$
\mathbb P(X \geq a) \leq E\left(\frac{X}{a}\right)=\frac{E(X)}{a}
$$

思路2

原始期望大于截断部分非负值的期望

求取期望时缩小$X$得到$a$

$$
\begin{aligned}
\mathbb{E}(X) &=\int_{-\infty}^{\infty} x f(x) d x \
& \geq \int_{a}^{\infty} x f(x) d x \quad(a \geq 0) \
& \geq \int_{a}^{\infty} a f(x) d x \
&=a \int_{a}^{\infty} f(x) d x \
&=a \mathbb{P}(X \geq a)
\end{aligned}
$$

图示

$a$越大于均值，$X>a$的概率越小

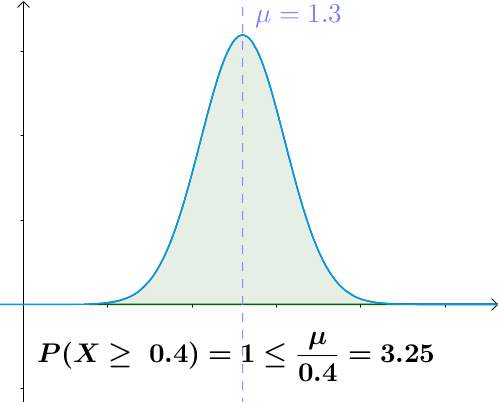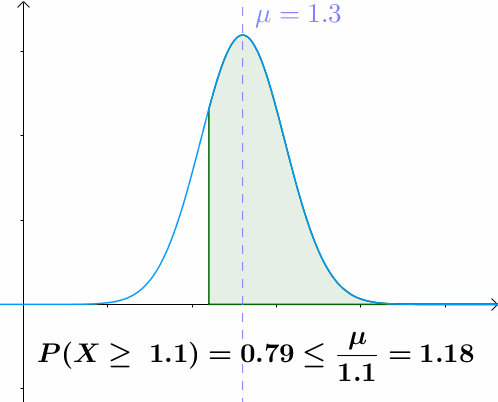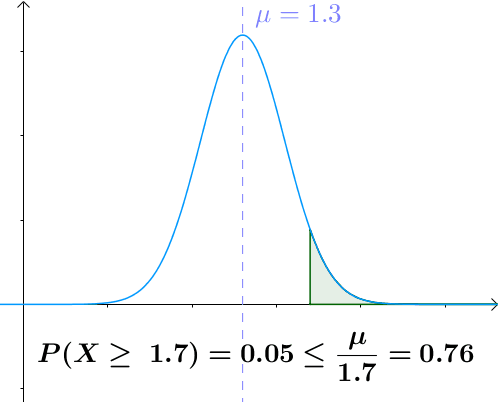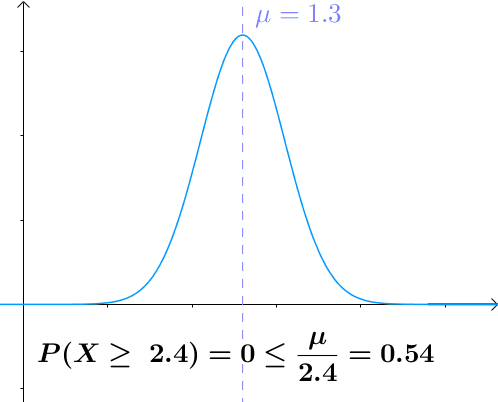
用途

• 将概率与期望联系起来建立了不等式关系
• 约束较松，可以用来粗略估计尾部事件

例如：

如果$X$是工资，那么$E(X)$就是平均工资，假设$a=n E(X)$，即平均工资的$n$倍。那么根据马尔可夫不等式，不超过$1/n$的人会有超过平均工资的$n$倍的工资。

参考资料

• https://baike.baidu.com/item/马尔可夫不等式/7565874?fr=aladdin

• https://www.zhihu.com/question/27821324

• https://blog.csdn.net/ukakasu/article/details/82688413

文章链接：
https://www.zywvvd.com/notes/study/probability/markov-inequality/markov-inequality/