最小二乘法与正态分布

最小二乘法由天文学的问题产生，由法国的数学家勒让德Legendre)创造，但也有人说是高斯(Gauss)创造的。本文记录最小二乘法的相关内容。

神说，要有正态分布，就有了正态分布。

神看正态分布是好的，就让随机误差服从了正态分布。

—— 创世纪—数理统计

最小二乘法的历史

17、18 世纪是科学发展的黄金年代，微积分的发展和牛顿万有引力定律的建立，直接的推动了天文学和测地学的迅猛发展。当时的大科学家们都在考虑许多天文学上的问题，这些天文学和测地学的问题，无不涉及到数据的多次测量、分析与计算；17、18 世纪的天文观测，也积累了大量的数据需要进行分析和计算。很多年以前，学者们就已经经验性的认为，对于有误差的测量数据，多次测量取算术平均是比较好的处理方法。虽然缺乏理论上的论证，也不断的受到一些人的质疑，取算术平均作为一种异常直观的方式，已经被使用了千百年, 在多年积累的数据的处理经验中也得到相当程度的验证，被认为是一种良好的数据处理方法。

问题的核心是，我们直接关心的目标量往往无法直接观测，但是一些相关的量是可以观测到的，而通过建立数学模型，最终可以解出我们关心的量。这些问题都可以用如下数学模型描述：我们想估计的量是 $β_0,⋯,β_p$, 另有若干个可以测量的量 $x_1,⋯,x_p,y$, 这些量之间有线性关系:
$$
y = \beta_0 + \beta_1x_1 + \cdots + \beta_px_p
$$
如何通过多组观测数据求解出参数$β_0,⋯,β_p$呢？ 欧拉和拉普拉斯采用的的方法都是求解如下线性方程组

$$ \begin{eqnarray} \left\{ \begin{array}{lll} y_1 = \beta_0 + \beta_1x_{11} + \cdots + \beta_px_{p1} \\ y_2 = \beta_0 + \beta_1x_{12} + \cdots + \beta_px_{p2} \\ \vdots \\ y_n = \beta_0 + \beta_1x_{1n} + \cdots + \beta_px_{pn} . \end{array} \right. \end{eqnarray} $$

但是面临的一个问题是，有 $n$ 组观测数据，$p+1$ 个变量， 如果 $n>p+1$, 则得到的线性矛盾方程组，无法直接求解。

所以欧拉和拉普拉斯采用的方法都是通过对数据的一定的观察，把$ n$个线性方程分为 $p+1$组，然后把每个组内的方程线性求和后归并为一个方程，从而就把$n$个方程的方程组化为$p+1$个方程的方程组，进一步解方程求解参数。这些方法初看有一些道理，但是都过于经验化, 无法形成统一处理这一类问题的通用解决框架。

最小化累计误差

有效的最小二乘法是勒让德在 1805 年发表的，基本思想就是认为测量中有误差，所以所有方程的累积误差为
$$
累积误差 =
∑
(
观测值 – 理论值
)
2
$$
我们求解出导致累积误差最小的参数就是利用当前数据对理论值的最优估计

$$ \begin{eqnarray} \label{least-square-error} \begin{array}{lll} \hat{\boldsymbol\beta}& = & \displaystyle \arg\min_{\boldsymbol {\beta}} \sum_{i=1}^n e_i^2 \\ & = & \displaystyle \arg\min_{\boldsymbol\beta} \sum_{i=1}^n\Bigl[y_i – (\beta_0 + \beta_1x_{1i} + \cdots + \beta_px_{pi})\Bigr]^2 . \end{array} \end{eqnarray} $$

提出最小二乘法

勒让德在论文中对最小二乘法的优良性做了几点说明：

1. 最小二乘法使得误差平方和最小，并在各个方程的误差之间建立了一种平衡，从而防止某一个极端误差取得支配地位；
2. 计算中只要求偏导后求解线性方程组，计算过程明确便捷；
3. 最小二乘法可以导出算术平均值作为估计值。

对于最后一点，推理如下：假设真值为 $θ, x_1,⋯,x_n$为 $n$ 次测量值, 每次测量的误差为 $e_i=x_i–θ$，按最小二乘法，误差累积为
$$
L(\theta) = \sum_{i=1}^n e_i^2 = \sum_{i=1}^n (x_i – \theta)^2
$$
求解$θ$使得$L(θ)$达到最小，正好是算术平均:
$$
\overline{x} = \frac{\sum_{i=1}^n x_i}{n}
$$
由于算术平均是一个历经考验的方法，而以上的推理说明，算术平均是最小二乘法的一个特例，所以从另一个角度说明了最小二乘法的优良性，使我们对最小二乘法更加有信心。

极大似然估计

1801 年 1 月，天文学家朱塞普 · 皮亚齐 (Giuseppe Piazzi, 1746-1826) 发现了一颗从未见过的光度 8 等的星在移动，这颗现在被称作谷神星（Ceres）的小行星在夜空中出现 6 个星期，扫过八度角后就在太阳的光芒下没了踪影，无法观测。而留下的观测数据有限，难以计算出他的轨道，天文学家也因此无法确定这颗新星是彗星还是行星，这个问题很快成了学术界关注的焦点。高斯当时已经是很有名望的年轻数学家了，这个问题引起了他的兴趣。高斯以其卓越的数学才能创立了一种崭新的行星轨道的计算方法，一个小时之内就计算出了谷神星的轨道，并预言了他在夜空中出现的时间和位置。 1801 年 12 月 31 日夜，德国天文爱好者奥伯斯 (Heinrich Olbers, 1758-1840)，在高斯预言的时间里，用望远镜对准了这片天空。果然不出所料，谷神星出现了！

高斯为此名声大震，但是高斯当时拒绝透露计算轨道的方法，原因可能是高斯认为自己的方法的理论基础还不够成熟，而高斯一向治学严谨、精益求精，不轻易发表没有思考成熟的理论。直到 1809 年高斯系统地完善了相关的数学理论后，才将他的方法公布于众，而其中使用的数据分析方法，就是以正态误差分布为基础的最小二乘法。那高斯是如何推导出误差分布为正态分布的？让我们看看高斯是如何猜测上帝的意图的。

设真值为 $θ, x_1,⋯,x_n$ 为 $n$ 次独立测量值, 每次测量的误差为 $e_i=x_i–θ$，假设误差 $e_i$ 的密度函数为$f(e)$, 则测量值的联合概率为 $n$ 个误差的联合概率，记为

$$ \begin{align*} L(\theta) & = L(\theta;x_1,\cdots,x_n)=f(e_1)\cdots f(e_n) \\ & = f(x_1-\theta)\cdots f(x_n-\theta) \end{align*} $$

但是高斯不采用贝叶斯的推理方式，而是直接取使 $ L(\theta) $ 达到最大值的 $ \hat{\theta}=\hat{\theta}\left(x_{1}, \cdots, x_{n}\right) $ 作为 $θ $的估计值，即
$$
\hat{\theta}= \arg\max_{\theta} L(\theta)
$$
现在我们把 $L(θ)$ 称为样本的似然函数，而得到的估计值 $ \hat{\theta} $ 称为极大似然估计。

高斯首次给出了极大似然的思想，这个思想后来被统计学家费希尔系统的发展成为参数估计中的极大似然估计理论。

高斯接下来的想法特别牛，他开始揣度上帝的意图，而这充分体现了高斯的数学天才。高斯把整个问题的思考模式倒过来：既然千百年来大家都认为算术平均是一个好的估计，那我就认为极大似然估计导出的就应该是算术平均！所以高斯猜测上帝在创世纪中的旨意就是：

误差分布导出的极大似然估计 = 算术平均值

正态分布

我们认识的高斯分布

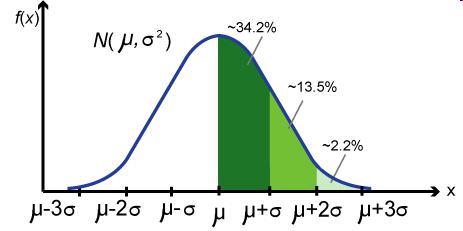
正态分布钟形的分布曲线不但形状优雅，它对应的密度函数写成数学表达式

$$ \displaystyle f(x)=\frac{1}{\sqrt{2\pi}\sigma}e^{-\frac{{(x-\mu})^2}{2\sigma^2}} $$

也非常具有数学的美感。其标准化后的概率密度函数

$$ \displaystyle f(x)=\frac{1}{\sqrt{2\pi}}e^{-\frac{x^2}{2}} $$

更加的简洁漂亮，两个最重要的数学常量 π、e 都出现在这公式之中。这个分布戴着神秘的面纱，在自然界中无处不在，让你在纷繁芜杂的数据背后看到隐隐的秩序。这个分布也称为高斯分布，正是由于高斯在推导最小二乘法过程中发现了这个分布。

极大似然之后

高斯去找迎合 误差分布导出的极大似然估计 = 算术平均值 这一猜想的密度函数 $f $ 。

即寻找这样的概率分布密度函数 $f$, 使得极大似然估计正好是算术平均 $\hat{\theta} = \overline{x}$。而高斯应用数学技巧求解这个函数$f$, 并且证明，所有的概率密度函数中，唯一满足这个性质的就是

$$ f(x)=\frac{1}{\sqrt{2\pi}\sigma}e^{-\frac{x^2}{2\sigma^2}} $$

正态分布的密度函数 $ N\left(0, \sigma^{2}\right) $ 就这样被高斯给解出来了!

高斯基于这个误差分布的密度函数对最小二乘法给出了一个很漂亮的解释。对于最小二乘公式中涉及的每个误差 $e_i$, 由于误差服从概率分布 $N(0,σ^2)$, 则$(e_1,⋯,e_n)$的概率密度为

$$ \frac{1}{(\sqrt{2\pi}\sigma)^n}\exp\left\{-\frac{1}{2\sigma^2} \sum_{i=1}^n e_i^2 \right\} . $$

要使得这个概率密度最大，必须使得 $\sum_{i=1}^n e_i^2 $ 取最小值，这正好就是最小二乘法的要求。

正态分布的推导过程

高斯以如下准则作为出发点
$$
误差分布导出的极大似然估计 = 算术平均值
$$
设真值为 $θ, x_1,⋯,x_n$为 $n$ 次独立测量值, 每次测量的误差为 $e_i=x_i–θ$，假设误差$e_i$的密度函数为 $f(e)$, 则测量值的联合概率密度为$n$个误差的联合概率，记为：

$$ \begin{align*} L(\theta) &= L(\theta;x_1,\cdots,x_n)=f(e_1)\cdots f(e_n) \\ & = f(x_1-\theta)\cdots f(x_n-\theta) \end{align*} $$

为求极大似然估计，令导数为 0
$$
\frac{d \log L(\theta)}{d \theta} = 0
$$
整理后可以得到
$$
\sum_{i=1}^n \frac{f’(x_i-\theta)}{f(x_i-\theta)} = 0
$$
令 $ g(x)=\frac{f^{\prime}(x)}{f(x)} $，则有
$$
\sum_{i=1}^n g(x_i-\theta) = 0
$$
由于高斯假设极大似然估计的解就是算术平均 $ \bar{x} = \frac{x_{1}+x_{2}+\ldots+x_{n}}{n} $ ，把解代入上式，可以得到
$$
\begin{equation} \sum_{i=1}^n g(x_i-\bar{x}) = 0 \quad \end{equation}
$$
该式对任意 $x_i$ 求偏导值均为零，即：
$$
\begin{equation} \frac{d \sum_{i=1}^n g(x_i-\bar{x})}{dx_i} = 0 \quad \end{equation}
$$
也就是说

$$ \begin{array}{l}g^{\prime}\left(x_{1}-\bar{x}\right)\left(1-\frac{1}{n}\right)+g^{\prime}\left(x_{2}-\bar{x}\right)\left(-\frac{1}{n}\right)+\ldots+g^{\prime}\left(x_{n}-\bar{x}\right)\left(-\frac{1}{n}\right)=0 \\ g^{\prime}\left(x_{2}-\bar{x}\right)\left(-\frac{1}{n}\right)+g^{\prime}\left(x_{2}-\bar{x}\right)\left(1-\frac{1}{n}\right)+\ldots+g^{\prime}\left(x_{n}-\bar{x}\right)\left(-\frac{1}{n}\right)=0 \\ \ldots \\ g^{\prime}\left(x_{1}-\bar{x}\right)\left(-\frac{1}{n}\right)+g^{\prime}\left(x_{2}-\bar{x}\right)\left(-\frac{1}{n}\right)+\ldots+g^{\prime}\left(x_{n}-\bar{x}\right)\left(1-\frac{1}{n}\right)=0\end{array} $$

我们可以将上述 $ n $ 个式子看作一个其次线性方程组，将 $ g^{\prime}\left(x_{i}-\bar{x}\right) $ 看作末知数向量，将系数提 取为一个 $ n \times n $ 的矩阵，则:

$$ \left[\begin{array}{cccc}1-\frac{1}{n} & -\frac{1}{n} & \ldots & -\frac{1}{n} \\ -\frac{1}{n} & 1-\frac{1}{n} & \ldots & -\frac{1}{n} \\ & & \cdot & \\ & & \cdot & \\ -\frac{1}{n} & -\frac{1}{n} & \ldots & 1-\frac{1}{n}\end{array}\right] \times\left[\begin{array}{c}g^{\prime}\left(x_{1}-\bar{x}\right) \\ g^{\prime}\left(x_{2}-\bar{x}\right) \\ \cdot \\ \cdot \\ \cdot \\ g^{\prime}\left(x_{n}-\bar{x}\right)\end{array}\right]=\left[\begin{array}{c}0 \\ 0 \\ \cdot \\ \cdot \\ \cdot \\ 0\end{array}\right] $$

求解这个齐次线性方程组可以得到一组通解：
$$
\mathbf{g}^{\prime}\left(x_{i}-\bar{x}\right)=c(1,1, \ldots 1)^{T}
$$
即对于任意 $x_i$ 有

$$ g^{\prime}\left(x_{1}-\bar{x}\right)=g^{\prime}\left(x_{2}-\bar{x}\right)=\ldots=g^{\prime}\left(x_{n}-\bar{x}\right)=c $$

等价于
$$
g^{\prime}\left(x\right)=c
$$
因此 $ g(x) $ 必然是一个线性方程: $ g(x)=c x+b $

又因为
$$
\sum_{i=1}^{n} g\left(x_{i}-\bar{x}\right)=\sum_{i=1}^{n} c\left(x_{i}-\bar{x}\right)+n b=0
$$
因此 $nb = 0$，即 $b=0$

最终我们得出了
$$
g(x)=\frac{f^{\prime}(x)}{f(x)}=c x
$$
将其转化为一阶线性微分方程的一般形式
$$
f^{\prime}(x)-(c x) f(x)=0
$$
求解这个微分方程得出
$$
f(x)=k e^{\frac{1}{2} c x^{2}}
$$
由于概率密度积分为1，对上式标准化后得到了正态分布的 PDF 0均值形式

$$ f(x)=\frac{1}{\sqrt{2 \pi} \sigma} e^{\frac{-x^{2}}{2 \sigma^{2}}} $$

上述过程证明了 最小二乘法得到的结果是真值的最佳估计 与 误差分布为正态分布 两个命题互为充要条件

$$ x=\bar{x} \Longleftrightarrow p(\epsilon)=\frac{1}{\sigma \sqrt{2 \pi}} e^{-\frac{\epsilon^{2}}{2 \sigma^{2}}} $$

中心极限定理

服从高斯分布的误差可以用最小二乘法估计真值，那误差的分布是正态分布吗

林德伯格 - 列维 中心极限定理

设 $ X_{1}, \cdots, X_{n} $ 独立同分布，且具有有限的均值 $ \mu $ 和方差 $ \sigma^{2} $ ，则在 $ n \rightarrow \infty $ 时, 有：
$$
\frac{\sqrt{n}(\bar{X}-\mu)}{\sigma} \rightarrow N(0,1)
$$
多么奇妙的性质，随意的一个概率分布中生成的随机变量，在序列和 (或者等价的求算术平均) 的操作之下，表现出如此一致的行为，统一的规约到正态分布。

假设独立随机变量序列 $X_i$ 的中值为 0, 要使序列和 $\displaystyle S=\sum_{i=1}^nX_i$ 的分布密度函数逼近正态分布，以下条件是充分必要的

1. 如果 $ X_{i} $ 相对于序列和 $ S $ 的散布 (也就是标准差) 是不可忽略的，则 $ X_{i} $ 的分布必须接近正态分布

2. 对于所有可忽略的 $ X_{i} $, 取绝对值最大的那一项，这个绝对值相对于序列和也是可忽略的

参考资料

• https://cosx.org/2013/01/story-of-normal-distribution-1
• https://cosx.org/2013/01/story-of-normal-distribution-2/
• https://zh.m.wikipedia.org/zh-cn/最小二乘法
• https://blog.csdn.net/The_lastest/article/details/82413772?share_token=04418df1-cfa5-4dec-b1d4-6dfeda9eca79
• https://blog.csdn.net/ccnt_2012/article/details/81127117
• https://zhuanlan.zhihu.com/p/379805764

文章链接：
https://www.zywvvd.com/notes/study/probability/least-square-normal-dis/least-square-normal-dis/