本文最后更新于:2025年4月30日 下午
本文介绍协方差。
协方差
协方差表示的是两个变量的总体的误差,这与只表示一个变量误差的方差不同。 如果两个变量的变化趋势一致,也就是说如果其中一个大于自身的期望值,另外一个也大于自身的期望值,那么两个变量之间的协方差就是正值。 如果两个变量的变化趋势相反,即其中一个大于自身的期望值,另外一个却小于自身的期望值,那么两个变量之间的协方差就是负值。 —— 百度百科
定义
- 在概率论和统计学中,协方差用于衡量两个变量的总体误差。而方差是协方差的一种特殊情况,即当两个变量是相同的情况。
- 期望值分别为$E[X]$与$E[Y]$的两个实随机变量$X$与$Y$之间的**协方差$Cov(X,Y)$定义为:
相关系数
- 定义随机变量$X$与$Y$的相关系数:
$$
\rho_{X Y}=\frac{\operatorname{Cov}[X, Y]}{\sqrt{\operatorname{Var}[X]} \sqrt{\operatorname{Var}[Y]}}
$$
- 相关系数是协方差的归一化
与方差的关系
- 由定义可知:
协方差的性质
-
$a, b$ 为常数,有:
$$
\operatorname{Cov}[a X, b Y]=a b \operatorname{Cov}[X, Y]
$$ -
变量和的协方差:
$$
\operatorname{Cov}\left[X_{1}+X_{2}, Y\right]=\operatorname{Cov}\left[X_{1}, Y\right]+\operatorname{Cov}\left[X_{2}, Y\right]
$$
- 连续变量的协方差:
$$
\operatorname{Cov}[f(X), g(Y)]=\mathbb{E}[(f(X)-\mathbb{E}[f(X)])(g(Y)-\mathbb{E}[g(Y)])]
$$
- 连续变量的协方差系数:
$$
\rho[f(X), g(Y)]=\frac{\operatorname{Cov}[f(X), g(Y)]}{\sqrt{\operatorname{Var}[f(X)]} \sqrt{\operatorname{Var}[g(Y)]}}
$$
协方差的物理意义
-
协方差的绝对值越大,说明两个随机变量都远离它们的均值
-
协方差为正,则说明两个随机变量同时趋向于取较大的值或者同时趋向于取较小的值
-
协方差为负,则说明一个随变量趋向于取较大的值,另一个随机变量趋向于取较小的值
-
两个随机变量的独立性可以导出协方差为零,但是两个随机变量的协方差为零无法导出独立性——正交-不相关-独立
因为独立性也包括:没有非线性关系
有可能两个随机变量是非独立的,但是协方差为零
如:假设随机变量 $X \sim U[-1,1]$。定义随机变量 的概率分布函数为:
$$
P(S=1)=\frac{1}{2} P(S=-1)=\frac{1}{2}
$$
定义随机变量 $Y=SX$,则随机变量$X,Y$是非独立的,但是有:
$$
Cov[X,Y]=0
$$
相关系数的物理意义
考虑以随机变量$X$的线性函数$a+bX$ 来近似表示$Y$。
- 均方误差,$e$为:
- e取极小值,该优化问题为凸优化,直接求导为0即可:
- 解得:
- 带入$e$得:
$$
\min (e)=\mathbb{E}\left[\left(Y-\left(a_{0}+b_{0} X\right)\right)^{2}\right]=\left(1-\rho_{X Y}^{2}\right) \operatorname{Var}[Y]
$$
-
因此有以下定理:
- $\left|\rho_{X Y}\right| \leq 1$
- $|\rho_{X Y}| = 1$的充要条件为:存在常数$a,b$使得$Y=a+bX$
-
当$\left|\rho_{X Y}\right|$较大时, $e$较小,意味着随机变量$X$和$Y$联系较紧密。于是$\rho_{X Y}$ 是一个表征 $X$、$Y$之间线性关系紧密程度的量
-
当$\rho_{X Y}=0$时,称$X$和$Y$ 不相关。
- 不相关是就线性关系来讲的,而相互独立是一般关系而言的。
- 相互独立一定不相关;不相关则未必独立。
协方差矩阵
- 设$n$维随机变量$(X_1,X_2, \dots,X_n)$的二阶混合中心矩
$$
c_{i j}=\operatorname{Cov}\left[X_{i}, X_{j}\right]=\mathbb{E}\left[\left(X_{i}-\mathbb{E}\left[X_{i}\right]\right)\left(X_{j}-\mathbb{E}\left[X_{j}\right]\right)\right]
$$
- 都存在,则称矩阵:
- 为$n$维随机变量$(X_1,X_2, \dots,X_n)$的协方差矩阵
- 由于$c_{ij} = c_{ji}$ 因此协方差矩阵是对称阵
- 由于对角线为各个变量的方差,因此对角线非负
- 通常$n$ 维随机变量的分布是不知道的,或者太复杂以致数学上不容易处理,因此实际中协方差矩阵非常重要。
多元正态分布与线性变换
假设一个向量$x$服从均值向量为$\mu$ 、协方差矩阵为$\Sigma$的多元正态分布(multi-variate Gaussian distribution),则
令该分布的均值向量为$\mu=\mathbf{0}$ ,由于指数项外面的系数$|2\pi\Sigma|^{-1/2}$通常作为常数,故可将多元正态分布简化为
$$ p\left(\boldsymbol{x}\right)\propto\exp\left(-\frac12\boldsymbol{x}^T\Sigma^{-1}\boldsymbol{x}\right) $$ 再令$\boldsymbol{x}=(y,z)^T$ ,包含两个随机变量 $y$ 和 $z$ ,则协方差矩阵可写成如下形式: $$ \Sigma=\begin{bmatrix}\sigma(y,y)&\sigma(y,z)\\\sigma\left(z,y\right)&\sigma(z,z)\end{bmatrix}\in\mathbb{R}^{2\times2} $$用单位矩阵(identity matrix) I 作为协方差矩阵,随机变量 y 和 z 的方差均为1,则生成如干个随机数如图1所示。
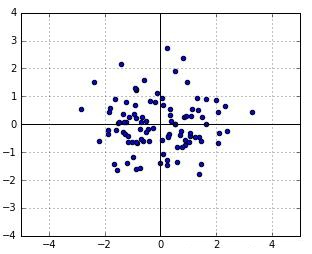
在生成的若干个随机数中,每个点的似然为
$$
\mathcal{L}\left(\boldsymbol{x}\right)\propto\exp\left(-\frac{1}{2}\boldsymbol{x}^{T}\boldsymbol{x}\right)
$$
对上图1中的所有点考虑一个线性变换(linear transformation):$ t=Ax$ ,我们能够得到下图2.

经过线性变换的二元正态分布,先将图1的纵坐标压缩0.5倍,再将所有点逆时针旋转30°得到。
在线性变换中,矩阵 A 被称为变换矩阵(transformation matrix),为了将图1中的点经过线性变换得到我们想要的图2,其实我们需要构造两个矩阵:
- 尺度矩阵(scaling matrix):
- 旋转矩阵(rotation matrix)
$$
R=\left[\begin{array}{cc}\cos(\theta)&-\sin(\theta)\\sin(\theta)&\cos(\theta)\end{array}\right]
$$
其中,$\theta$为顺时针旋转的度数。
变换矩阵、尺度矩阵和旋转矩阵三者的关系式:
$$
A=RS
$$
另外,需要考虑的是,经过了线性变换 $t$ 的分布是什么样子
将 $\boldsymbol{x}=A^{-1}\boldsymbol{t}$ 带入前面给出的似然 $\mathcal{L}\left(\boldsymbol{x}\right)$, 有
$$ \mathcal{L}\left(\boldsymbol{t}\right)\propto\exp\left(-\frac{1}{2}\left(A^{-1}\boldsymbol{t}\right)^{T}\left(A^{-1}\boldsymbol{t}\right)\right) =\exp\left(-\frac{1}{2}\boldsymbol{t}^{T}\left(AA^{T}\right)^{-1}\boldsymbol{t}\right) $$ 由此可以得到,多元正态分布的协方差矩阵为 $$ \Sigma=AA^{T}= \begin{bmatrix} {\frac{\sqrt{3}}{2}} & {\frac{1}{4}} \\ {-\frac{1}{2}} & {\frac{\sqrt{3}}{4}} \end{bmatrix} \begin{bmatrix} {\frac{\sqrt{3}}{2}} & {-\frac{1}{2}} \\ {\frac{1}{4}} & {\frac{\sqrt{3}}{4}} \end{bmatrix}= \begin{bmatrix} {\frac{13}{16}} & {-\frac{3\sqrt{3}}{16}} \\ {-\frac{3\sqrt{3}}{16}} & {\frac{7}{16}} \end{bmatrix}. $$协方差矩阵的特征值分解
回到我们已经学过的线性代数内容,对于任意对称矩阵 $Σ$ ,存在一个特征值分解(eigenvalue decomposition, EVD):
$$
Σ=UΛU^T
$$
其中,$U$ 的每一列都是相互正交的特征向量,且是单位向量,满足 $U^TU=I$ ,$Λ$ 对角线上的元素是从大到小排列的特征值,非对角线上的元素均为0。
当然,这条公式在这里也可以很容易地写成如下形式:
$$ \Sigma= \begin{pmatrix} U\Lambda^{1/2} \end{pmatrix} \begin{pmatrix} U\Lambda^{1/2} \end{pmatrix}^T=AA^T $$其中,$A=U\Lambda^{1/2}$ ,因此,通俗地说,任意一个协方差矩阵都可以视为线性变换的结果。
在上面的例子中,特征向量构成的矩阵为
$$ U=R= \begin{bmatrix} {\cos(\theta)} & {-\sin(\theta)} \\ {\sin(\theta)} & {\cos(\theta)} \end{bmatrix}= \begin{bmatrix} {\frac{\sqrt{3}}{2}} & {\frac{1}{2}} \\ {-\frac{1}{2}} & {\frac{\sqrt{3}}{2}} \end{bmatrix}. $$ 特征值构成的矩阵为 $$ \Lambda=SS^{T}= \begin{bmatrix} {s_{y}^{2}} & {0} \\ {0} & {s_{z}^{2}} \end{bmatrix}= \begin{bmatrix} {1} & {0} \\ {0} & {\frac{1}{4}} \end{bmatrix}. $$到这里,我们发现:多元正态分布的概率密度是由协方差矩阵的特征向量控制旋转(rotation),特征值控制尺度(scale),除了协方差矩阵,均值向量会控制概率密度的位置,在图1和图2中,均值向量为 0 ,因此,概率密度的中心位于坐标原点。
- 笔记:
- 每个样本可以理解为一个p维的随机向量。同时,每个维度可以理解为一个随机变量。样本的协方差矩阵说的是,p个随机变量之间的协方差,所构成的矩阵。
- 由于有p个随机变量,因此样本的协方差矩阵为p×p;
- 样本的协方差矩阵如何计算?(每个样本都对协方差矩阵贡献了自己的方差),所以是这样算的:永远在你身后:PCA(主成分分析)原理推导
- 协方差矩阵和PCA之间的关系是啥?$w^T$样本的协方差矩阵$*w$就是样本投影到 $w$ 这个方向上的方差;而PCA就是最大化这个方差(方差可以理解为信息,尽可能多的保留信息)
- 如何理解投影后方差这个公式,可以协方差矩阵当成一个线性系统。线性系统左乘了一个行向量 $w$,代表啥?右乘了一个投影向量又代表啥?
- 协方差刻画的是,两个随机变量之间的相关性,还是相似性(答案是相似性,peason相关,请复习peason相关)?
参考资料
文章链接:
https://www.zywvvd.com/notes/study/probability/covariance/covariance/
“觉得不错的话,给点打赏吧 ୧(๑•̀⌄•́๑)૭”

微信支付

支付宝支付