牛顿—莱布尼兹公式

本文最后更新于：2023年12月5日下午

牛顿—莱布尼兹公式描述了定积分和不定积分的关系。

牛顿—莱布尼兹公式

牛顿—莱布尼兹公式描述了定积分和不定积分的关系．我们已知不定积分是求导的逆运算，而定积分是函数曲线与 $x$ 轴之间的面积，二者乍看起来没什么联系，但牛顿—莱布尼兹公式却揭示了了二者之间的重要关系．

若 $ F(x) $ 是 $ f(x) $ 的一个原函数，则：
$$
\int_{a}^{b} f(x) \mathrm{d} x=F(b)-F(a)
$$

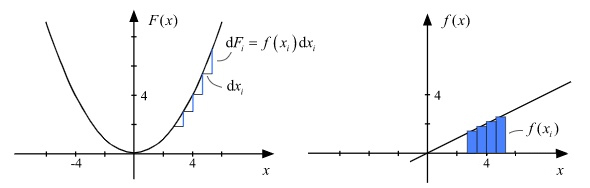
如图，根据定积分的定义：

$$ \int_{a}^{b} f(x) \mathrm{d} x=\lim _{\Delta x_{i} \rightarrow 0} \sum_{i} f\left(x_{i}\right) \Delta x_{i} $$

其中 $ f\left(x_{i}\right) \Delta x_{i} $ 可看成是右图中第 $ i $ 个小矩形的面积，求和是对从 $ a $ 到 $ b $ 的所有小矩形求和. 现在不妨把 $ x_{i} $ 设为第 $ i $ 个小矩形左端的 $ x $ 坐标. 考虑到求导是不定积分的逆运算，有 $ f\left(x_{i}\right)=F^{\prime}\left(x_{i}\right) $ ，所以小矩形的面积变为
$$
f\left(x_{i}\right) \Delta x_{i}=F^{\prime}\left(x_{i}\right) \Delta x_{i} \approx \Delta F_{i}=F\left(x_{i+1}\right)-F\left(x_{i}\right)
$$
最后一步使用了微分近似. 该式可以理解成，右图中的小矩形面积约等于左图中的小竖线长度，原函数 $F(x)$ 在 $x_i$ 到 $x_{i+1}$ 间的增量。当取极限 $\Delta x_{i} \rightarrow 0 $ 时，上式取等号

$$ \int_{a}^{b} f(x) \mathrm{d} x=\lim _{\Delta x_{i} \rightarrow 0} \sum_{i}\left[F\left(x_{i+1}\right)-F\left(x_{i}\right)\right]=F(b)-F(a) $$

该式可理解为，如果把左图中每一段 $ \Delta x_{i} $ 所对应的微小增量 $ \Delta F_{i} $ 都加起来，再取极限 $ \Delta x_{i} \rightarrow 0 $ ，就是 $ F(x) $ 从 $ a $ 到 $ b $ 的总增量. 在计算定积分的过程中，为了书写简洁，我们往往将上式中的 $ F(b)-F(a) $ 记为 $ \left.F(x)\right|_{a} ^{b} $.

推导

定义一个变上限积分函数 $ \Phi(x)=\int_{a}^{x} f(t) \mathrm{d} t $ ，让函数 $ \Phi(x) $ 获得增量 $ \Delta x $ ，则对应的函数增量：
$$
\int_{a}^{x+\Delta x} f(t) \mathrm{d} t-\int_{a}^{x} f(t) \mathrm{d} t=\int_{x}^{x+\Delta x} f(t) \mathrm{d} t
$$
根据积分中值定理：
$$
\Delta \Phi=\int_{x}^{x+\Delta x} f(t) \mathrm{d} t=f(\xi) \Delta x ， \quad(\mathrm{x} \le \xi \le \mathrm{x}+\Delta \mathrm{x})
$$

$$
\lim _{\Delta x \rightarrow 0} \frac{\Delta \Phi}{\Delta x}=\lim _{\Delta x \rightarrow 0} \frac{f(\xi) \Delta x}{\Delta x}=\lim _{\Delta x \rightarrow 0} f(\xi)=\lim _{\xi \rightarrow x} f(\xi)=f(x)
$$

所以：
$$
\Phi^{\prime}(x)=f(x), \quad \Phi(x)=F(x)+C
$$
因为：
$$
\begin{array}{c}
\Phi(a)=C+F(a)=0\
C=-F(a)\
\Phi(x)+F(a)=F(x)
\end{array}
$$
因此：
$$
\Phi(b)=F(b)-F(a)
$$

$$
\int_{a}^{b} f(x) d x=F(b)-F(a)
$$

算例

定积分上下限求导

$$
\frac{\mathrm{d}}{\mathrm{d} x} \int_{a}^{x} f(t) \mathrm{d} t
$$

我们可以先对定积分用牛顿莱布尼兹公式，令原函数为 $ F(x) $ ，有：
$$
\frac{\mathrm{d}}{\mathrm{d} x} \int_{a}^{x} f(t) \mathrm{d} t=\frac{\mathrm{d}}{\mathrm{d} x}[F(x)-F(a)]=f(x)
$$
类似地，对积分下限求导如：
$$
\frac{\mathrm{d}}{\mathrm{d} x} \int_{x}^{a} f(t) \mathrm{d} t=\frac{\mathrm{d}}{\mathrm{d} x}[F(a)-F(x)]=-f(x)
$$
对上下限同时求导如：
$$
\frac{\mathrm{d}}{\mathrm{d} x} \int_{-x}^{x} f(t) \mathrm{d} t=\frac{\mathrm{d}}{\mathrm{d} x}[F(x)-F(-x)]=f(x)+f(-x)
$$