蒙特卡洛（Monte Carlo）方法

本文最后更新于：2024年5月7日下午

蒙特卡洛方法可以近似计算某个概率值，计算结果随着实验次数增加而愈加精确，本文记录相关内容。

简介

蒙特卡洛方法Monte Carlo 可以通过采用随机投点法来求解不规则图形的面积。

求解结果并不是一个精确值，而是一个近似值。当投点的数量越来越大时，该近似值也越接近真实值。
蒙特卡洛方法也可以用于根据概率分布来随机采样的任务。

布丰投针

布丰投针问题是1777年法国科学家布丰提出的一种计算圆周率的方法：随机投针法。

执行步骤

首先取一张白纸，在上面绘制许多条间距为$d$ 的平行线。
取一根长度为$l , l \lt d$的针，随机地向纸上投掷$n$次，观测针与直线相交的次数，记做 $m$。
计算针与直线相交的概率 $p=\frac{m}{n}$。因此有：

$$
\pi = 2 \frac { n \times l } { m \times d }
$$

相交概率证明

由于向纸上投针是完全随机的, 因此用二维随机变量 $ (X, Y) $ 来确定针在纸上的具体位置。其中:

$ X $ 表示针的中点到平行线的距离，它是 $ [0, d / 2] $ 之间的均匀分布。
$ Y $ 表示针与平行线的夹角，它是 $ \left[0, \frac{\pi}{2}\right] $ 之间的均匀分布。

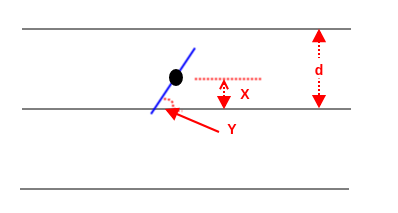
当 $ X<\frac{l}{2} \sin Y $ 时，针与直线相交。
由于 $ X, Y $ 相互独立，因此有概率密度函数：

$$ p(X=x, Y=y)=\left\{\begin{array}{ll} \frac{4}{\pi d}, & 0 \leq x \leq d / 2,0 \leq y \leq \pi / 2 \\ 0, & \text { else } \end{array}\right. $$

因此，针与直线相交的概率为：

$$ \begin{array}{c} P \left\{X<\frac{l}{2} \sin Y\right\} &= & \iint_{x<\frac{l}{2} \sin y} p(x, y) d x d y\\ &=& \int _ { x = 0 } ^ { x = \frac{1}{2} \sin y } \int_{y=0}^{ y = \pi / 2} \frac {4}{ \pi d} d x d y\\ &=& \frac{ 2l }{ \pi d } \end{array} $$

根据 $ \frac{2 l}{\pi d}=\frac{m}{n} $ 即可得证。

蒙特卡洛积分

对于函数 $ f(x) $, 其在区间 $ [a, b] $ 上的积分 $ \int_{a}^{b} f(x) d x $ 可以采用两种方法来求解: 投点法、期望法。

投点法

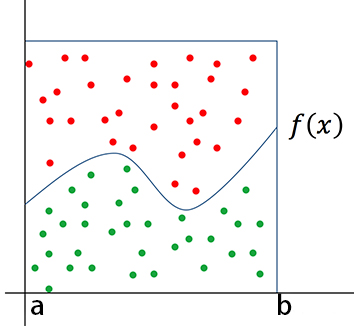
对函数 $ f(x) $, 对其求积分等价于求它的曲线下方的面积。
定义一个常数 $M$，使得 $ M>\max _{a \leq x \leq b} f(x) $，该常数在区间 $ [a, b] $上的面积就是矩形面积 $ M(b-a) $.
随机向矩形框中随机的、均匀的投点，设落在函数$ f(x) $下方的点为绿色，落在$ f(x) $和$M$之间的点为红色。
则有：落在$ f(x) $下方的点的概率等于$ f(x) $的面积比上矩形框的面积 。
从 $ [a, b] $ 之间的均匀分布中采样 $ x_{0} $, 从 $ [0, M] $ 之见的均匀分布中采样 $ y_{0}, \quad\left(x_{0}, y_{0}\right) $ 构成一个随机点。
若 $ y_{0} \leq f\left(x_{0}\right) $, 则说明该随机点在函数 $ f(x) $ 下方，染成绿色。
若 $ f\left(x_{0}\right)<y_{0} \leq M $, 则说明该随机点在函数 $ f(x) $ 上方，染成红色。
假设绿色点有$n_1$个，红色点有$n_2$个，总的点数为$n_1 + n_2$ ，因此有：

$$
\int_{a}^{b} f(x) d x=\frac{n_{1}}{n_{1}+n_{2}} \times M(b-a)
$$

期望法

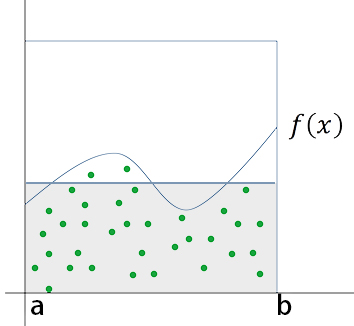
假设需要求解积分$ I=\int_{a}^{b} f(x) d x $，则任意选择一个概率密度函数 $ p(x) $，其中$ p(x) $满足条件:

$$ \begin{array}{c} \int_{a}^{b} p(x) d x=1 \\ \text { if } f(x) \neq 0 \text { then } p(x) \neq 0, \quad a \leq x \leq b \end{array} $$

令:

$$ f^{*}(x)=\left\{\begin{array}{ll} \frac{f(x)}{p(x)}, & p(x) \neq 0 \\ 0, & p(x)=0 \end{array}\right. $$

则有:

$$
I=\int_{a}^{b} f(x) d x=\int_{a}^{b} f^{*}(x) p(x) d x
$$

$I$刚好是一个期望：设随机变量 $ X $ 服从分布 $ X \sim p(x) $, 则 $ I=\mathbb{E}_{X \sim p}\left[f^{*}(X)\right] $
则期望法求积分的步骤是：
- 任选一个满足条件的概率分布 $ p(x) $ 。
- 根据 $ p(x) $, 生成一组服从分布 $ p(x) $ 的随机数 $ x_{1}, x_{2}, \cdots, x_{N} $ 。
- 计算均值 $ \bar{I}=\frac{1}{N} \sum_{i=1}^{N} f^{*}\left(x_{i}\right) $, 并将 $ \bar{I} $ 作为 $ I $ 的近似。
在期望法求积分中, 如果 $ a, b $ 均为有限值, 则 $ p(x) $ 可以取均匀分布的概率密度函数：

$$ p(x)=\left\{\begin{array}{ll}\frac{1}{b-a}, & a \leq x \leq b \\ 0, & \text { else }\end{array}\right. $$

	此时 $ f^{*}(x)=(b-a) f(x), \quad \bar{I}=\frac{b-a}{N} \sum_{i=1}^{N} f\left(x_{i}\right) $ 。

其物理意义为: $ \frac{\sum_{i}^{N} f\left(x_{i}\right)}{N} $ 为在区间 $ [a, b] $ 上函数的平均高度, 乘以区间宽度 $ b-a $ 就是平均面积。

蒙特卡洛采样

采样问题的主要任务是：根据概率分布 $ p(x) $, 生成一组服从分布 $ p(x) $ 的随机数 $ x_{1}, x_{2}, \cdots . $

均匀分布模拟$p(x)$采样

如果 $ p(x) $ 就是均匀分布，则均匀分布的采样非常简单。
如果 $ p(x) $ 是非均匀分布，则可以通过均匀分布的采样来实现。

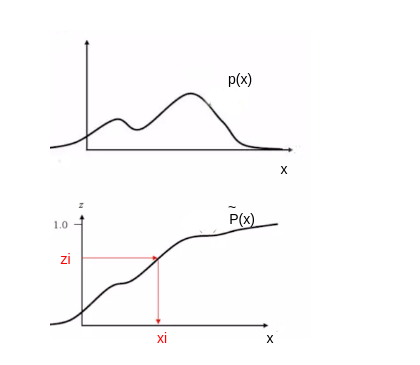
首先根据均匀分布 $ U(0,1) $ 随机生成一个样本 $ z_{i} $ 。
设 $ \tilde{P}(x) $ 为概率分布 $ p(x) $ 的累计分布函数:

$$
\tilde{P}(x)=\int_{-\infty}^{x} p(z) d z
$$

令 $ z_{i}=\tilde{P}\left(x_{i}\right) $, 计算得到 $ x_{i}=\tilde{P}^{-1}\left(z_{i}\right) $, 其中 $ \tilde{P}^{-1} $ 为反函数, 则 $ x_{i} $ 为对 $ p(x) $ 的采样。

通过均匀分布的采样的原理：假设随机变量$ Z, X $ 满足 $ Z=\tilde{P}(X) $, 则 $ X $ 的概率分布为:

$$
p_{Z}(z) \frac{d}{d x} \tilde{P}(x)
$$

因为 $ Z $ 是 $ [0,1] $ 上面的均匀分布，因此 $ p_{Z}(z)=1 ; \tilde{P}(x) $ 为概率分布 $ p(x) $ 的累计分布函数, 因此 $ \frac{d}{d x} \tilde{P}(x)=p_{X}(x) $ 。因此上式刚好等于 $ p(x) $, 即： $ x_{i} $ 服从概率分布 $ p(x) $ 。

这其中有两个关键计算：

根据 $ p(x) $, 计算累计分布函数 $ \tilde{P}(x)=\int_{-\infty}^{\pi} p(z) d z $ 。
根据 $ z=\tilde{P}(x) $ 计算反函数 $ x=\tilde{P}^{-1}(z) $ 。

如果累计分布函数无法计算，或者反函数难以求解，则该方法无法进行。

接受-拒绝采样

对于复杂的概率分布$p(x)$ ，难以通过均匀分布来实现采样。此时可以使用接受-拒绝采样 策略。

首先选定一个容易采样的概率分布 $ q(x) $ ，选择一个常数 $ k $, 使得在定义域的所有位置都满足 $ p(x) \leq k \times q(x) $ 。
然后根据概率分布 $ q(x) $ 随机生成一个样本 $ x_{i} $ 。
计算 $ \alpha_{i}=\frac{p\left(x_{i}\right)}{k q\left(x_{i}\right)} $, 以概率 $ \alpha_{i} $ 接受该样本。

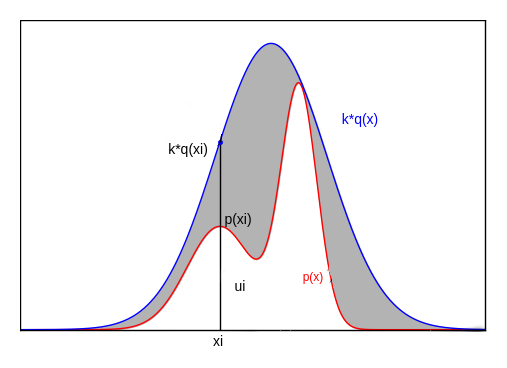
方法一

根据均匀分布$ U(0,1) $随机生成一个点 $ u_{i} $，如果 $ u_{i} \leq \alpha_{i} $，则接受该样本；否则拒绝该样本。

方法二

根据均匀分布 $ U\left(0, k q\left(x_{i}\right)\right) $ 生成一个随机点, 如果该点落在灰色区间$((p(x_{i}), k q(x_{i})]) $则拒绝该样本；如果该点落在白色区间$ \left(\left[0, p\left(x_{i}\right)\right]\right) $则接受该样本。