希尔伯特曲线 Hilbert Curve

本文最后更新于：2024年5月7日下午

希尔伯特曲线是一条填满整个平面的神奇曲线，可以理解为一种线段和正方形平面的一一映射，本文记录相关内容。

简介

希尔伯特曲线（Hilbert Curve）是一种连续的空间填充曲线，具有多个回旋和折叠的特点。它最初由德国数学家David Hilbert于1891年引入，并在之后的数学研究中广泛应用。希尔伯特曲线的独特之处在于它具有无限长度，但能以有限的空间覆盖整个平面。因此，希尔伯特曲线广泛应用于计算机科学、物理学、遥感、生物信息学等领域，用于分形分析、地图制作、信号处理等方面。

定义

其构造方式是把前一阶的曲线复制四份, 将左下角和右下角的曲线做一个沿对角线的翻转, 然后增加三条线段把这四份连起来.这些曲线的极限就是希尔伯特曲线。

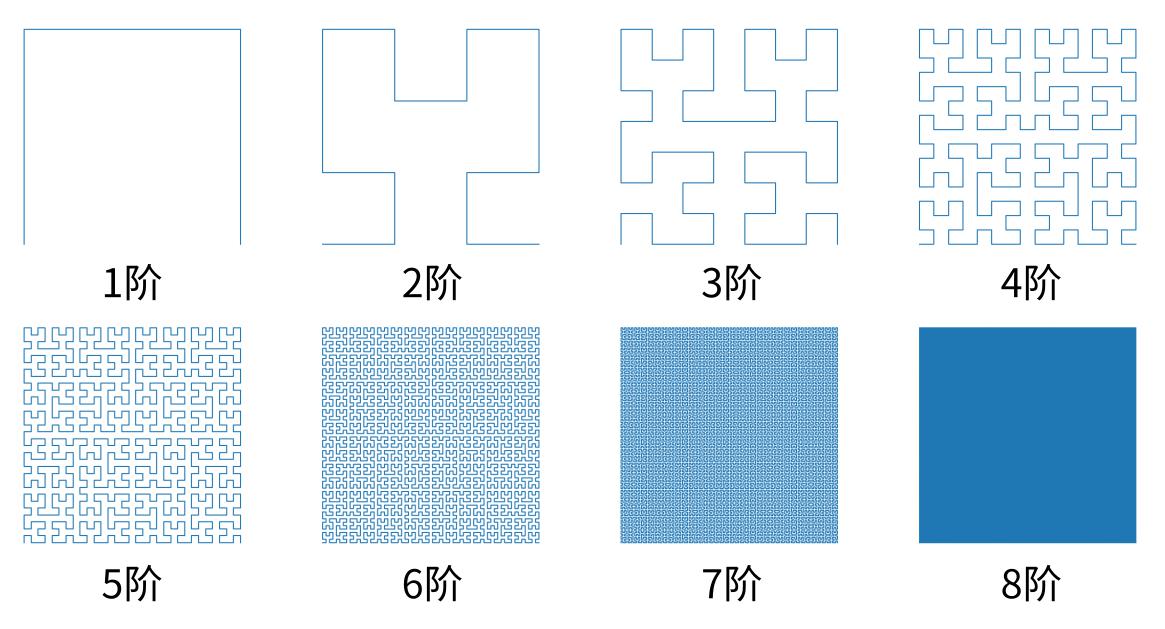
希尔伯特曲线一种能填充满一个平面正方形的分形曲线（空间填充曲线）。由于它能填满平面，它的豪斯多夫维是2。取它填充的正方形的边长为1，第 $n$ 步的希尔伯特曲线的长度是 $2^n - 2^{-n}$。

$ n $ 阶的希尔伯特曲线是从 $ [0,1] $ 区间到 $ [0,1] \times[0,1] $ 平面区域的映射 $ f_{n} $ ，把 0 和 1 映射到区域左下角和右下角:

$$
f_{n}(0)=(0,0), \quad f_{n}(1)=(1,0)
$$
并且, 通过适当的调整,让每个 1/4 的小区间映射到 4 个区域内.

填充整个区域的希尔伯特曲线是这样的函数 $f$, 使得函数列 $f_n$ 逐点收敛到它. 即:

$$ f(x):=\lim _{n \rightarrow \infty} f_{n}(x) $$

曲线性质

良定义

首先要说明这个定义是 well-defined , 即对于所有的 $x$, $f_n(x)$ 确实收敛。我认为这个可以从区间来说明。不管 $x$ 取定义域中的什么值, 都可以不断将区间四等分, 用长度为$1/4,1/16,1/64$的区间套来套住, 由于不同阶 Hilbert 曲线的定义, 对应的函数值也落在相应的区域套内. 这样形成一系列闭区域的套, 总有一个确定的极限值.

这里有个问题就是,当 $x$ 是两个四等分区间的交点时应该取左边的区间继续等分,还是取右边的区间继续等分. 这里应该能够证明取哪个得到的极限都是一样的, 这也是曲线连续性的要求.

填充整个区间

Hilbert 函数的取值遍布整个单位平面区域. 在 $[0,1]×[0,1]$ 里面随便选一个点 $(x,y)$ , 将平面不断四等分为上下左右四个闭区域, 用同样的方法, 能对应到定义域里的闭区间, 最后套出一个自变量 $x_0$ 来, 使得 $f(x_0)=(x,y)$.

这里要是选择的点落在边界上应该选哪个区域继续四等分呢? 这时选不同的点就不一样了. 比如 $(1/2,0)$点, 其实会有左右两个 $x$ ,都能逼近这个点. 这恰恰说明, Hilbert 曲线, 是满射(映上的), 不是单射(1-1的), 所以也不是双射.

仍然是曲线

曲线要求是 $[0,1]$ 到 $R^2$ 上的连续映射. 这里的连续性还比较好说. 对于值域中的点 $(x,y)$, 选择一个任意小的 $ϵ$ 邻域, 都可以在里面找到更小的$1/4 ^ k × 1/ 4 ^ k$ 大的(对齐的)闭区域, 对应到定义域是一个闭区间, 然后找到更小的 $δ$ 开区间, 这里的所有点都会映射到 $ ϵ$ 领域中.

因为 Hilbert 曲线不是单射, 故不存在逆映射. 不能说 Hilbert 曲线让直线段和平面区域拓扑同胚了.

生成过程

考虑一个 $1\times1$ 的正方形，通过希尔伯特曲线映射到 $(0,1)$ 区间

一阶

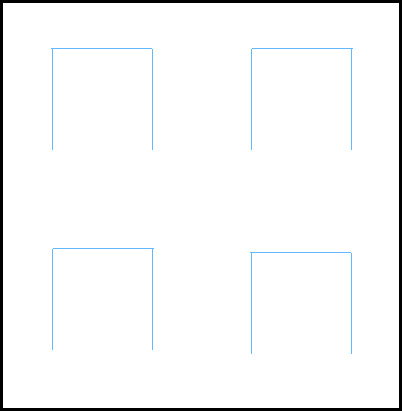
一阶的希尔伯特曲线，生成方法就是把正方形四等分，从其中一个子正方形的中心开始，依次穿线，穿过其余3个正方形的中心。

升阶

已经生成了上一阶希尔伯特曲线后生成下一阶，需要：

把之前每个子正方形继续四等分，每4个小的正方形先生成上一阶阶希尔伯特曲线；
每个小的四等分中第三第四象限的曲线分别沿两个对角线翻转；
添加三条线段把 4 个上一阶的希尔伯特曲线首尾相连。

四等分生成上一阶曲线

第三第四象限对角线翻转

添加三条线段

把 4 个上一阶的希尔伯特曲线首尾相连

这样就生成了下一阶希尔伯特曲线，以此类推，可以在 $1\times1$ 内生成无限阶希尔伯特曲线填满空间。

映射顺序

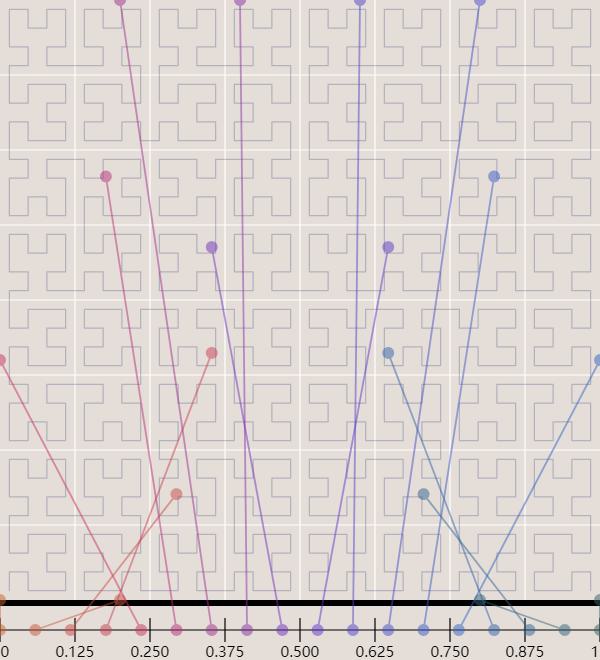
由于希尔伯特曲线是不断四等分划分而来，而且保持了固定的穿线顺序，因此没有处于边界上的二维点会被稳定地映射到一维线段中对应的某一段：

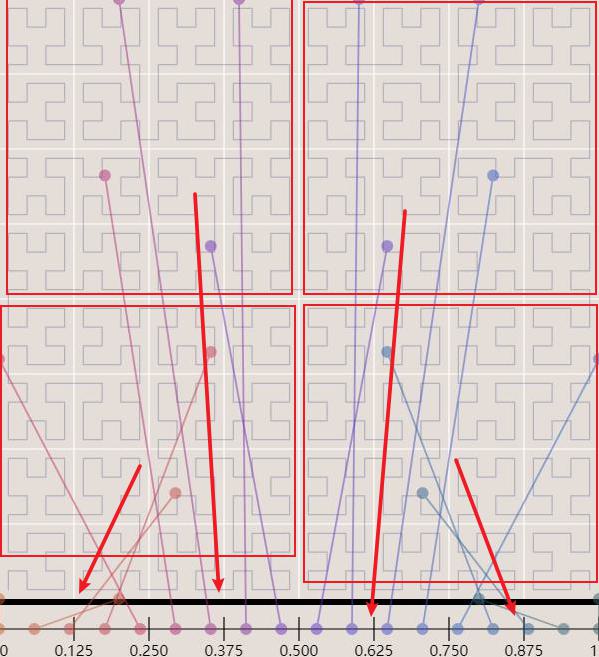
这样二维映射时就保证了一定的顺序，但处于分界线上的点事实上是双射，无法保证顺序了：

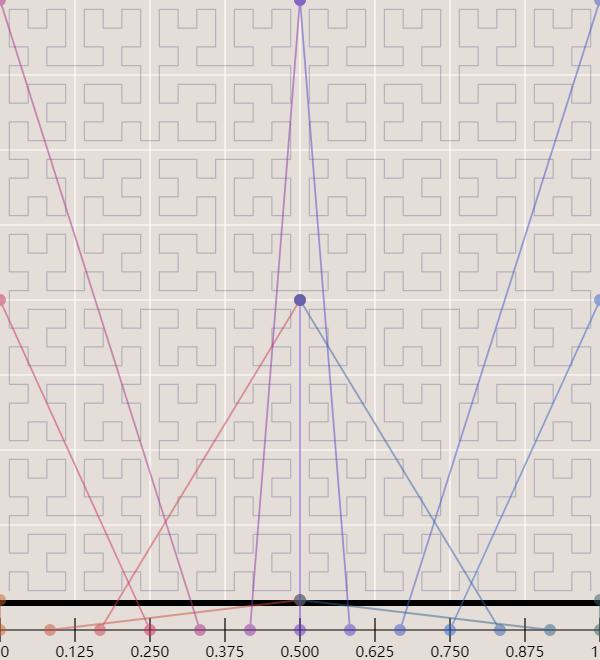
曲线长度

$n$ 阶希尔伯特曲线长度为 $2^n - 2^{-n}$，这里给出我个人的计算方法：

线段个数

首先我计算 $n$ 阶希尔伯特曲线的线段个数 $M_n$，根据定义：

$$ \begin{array}{c} M_1 = 3\\ M_{n+1} = 4M_n + 3 \end{array} $$

可以得到：

$$ \begin{array}{c} \frac{M_{n+1} + 1}{M_{n} + 1} = 4\\ M_{1}+1 = 4 \end{array} $$

即 $M_{k} + 1$ 是首项为 4，公比为 4 的等比数列，因此：

$$ \begin{array}{c} {M_{n} + 1} = 4^n\\ M_{n}=4^n-1 \end{array} $$

即 $n$ 阶希尔伯特曲线线段个数为 $M_n=4^n-1$

线段长度

紧贴曲线

如果希尔伯特曲线边缘紧贴 $1 \times 1$ 的正方形，如下图所示：

则一阶的曲线线段长度为 1，设此时第 $n$ 阶曲线的线段将边长1的长度拆分为 $C_n$ 份，则 $n+1$ 阶会将 1 拆分为 $2C_n+1$ 份，即：
$$
C_{n+1}=2C_n+1
$$
同样的等比数列，可以推导得到 $n$ 阶曲线将边长 1 拆分为 $C_n=2^n-1$ 份。

因此当希尔伯特曲线边缘紧贴正方形边缘时 $n$ 阶曲线的线段边长 $E_n$ 为：
$$
E_n=\frac{1}{C_n}=\frac{1}{2^n-1}
$$

真实曲线

考虑真实的希尔伯特曲线，其本身相当于把上文的紧贴曲线进行缩放某一个倍率，可以轻易得到第 $n$ 阶曲线会将紧贴曲线缩小 $S_n = \frac{2^n-1}{2^n}$ 倍。

曲线长度

结合上述结论，我们可以计算 $n$ 阶希尔伯特曲线的长度了，这里用$L_n$ 表示：

$$ \begin{array}{c} L_n &=&M_nE_nS_n\\ &=&(4^n-1)(\frac{1}{2^n-1})(\frac{2^n-1}{2^n})\\ &=&2^n-2^{-n} \end{array} $$

曲线绘制

这里贴一段 ChatGPT4 写的一段 python 绘制希尔伯特曲线的代码，为了显示大方好看一点，一些参数我做了修改：

import turtle

def hilbert_curve(turtle, level, angle, step):
    if level == 0:
        return
    turtle.right(angle)
    hilbert_curve(turtle, level - 1, -angle, step)
    turtle.forward(step)
    turtle.left(angle)
    hilbert_curve(turtle, level - 1, angle, step)
    turtle.forward(step)
    hilbert_curve(turtle, level - 1, angle, step)
    turtle.left(angle)
    turtle.forward(step)
    hilbert_curve(turtle, level - 1, -angle, step)
    turtle.right(angle)

turtle.setup(400, 400)
turtle.penup()
turtle.goto(-140, 140)
turtle.pendown()
hilbert_curve(turtle, 3, 90, 40)
turtle.done()

绘制过程：

二维排序应用

可以将二维平面上若干点映射到希尔伯特曲线上，按照点在曲线上的位置距离进行排序：

import numpy as np 
from hilbertcurve.hilbertcurve import HilbertCurve

def points_sort(points_array):
    BITS_PER_DIM = 16
    scaled_points = (points_array * (2**BITS_PER_DIM - 1)).astype('int64')
    # Create a Hilbert curve object with the specified number of bits per dimension
    hilbert_curve = HilbertCurve(BITS_PER_DIM, 2)
    # Map the 2D points to 1D values using the Hilbert curve
    hilbert_values = np.array([hilbert_curve.distance_from_point(p) for p in scaled_points])
    # Sort the points by their Hilbert values
    sorted_indices = np.argsort(hilbert_values)
    sorted_points = points_array[sorted_indices]
    return sorted_points