本文最后更新于:2024年5月7日 下午
本文将讨论推土机距离 Earth Mover’s Distance (EMD),和欧式距离一样,它们都是一种距离度量的定义、可以用来测量某两个分布之间的距离。本文记录推土机距离相关内容。
推土机距离
-
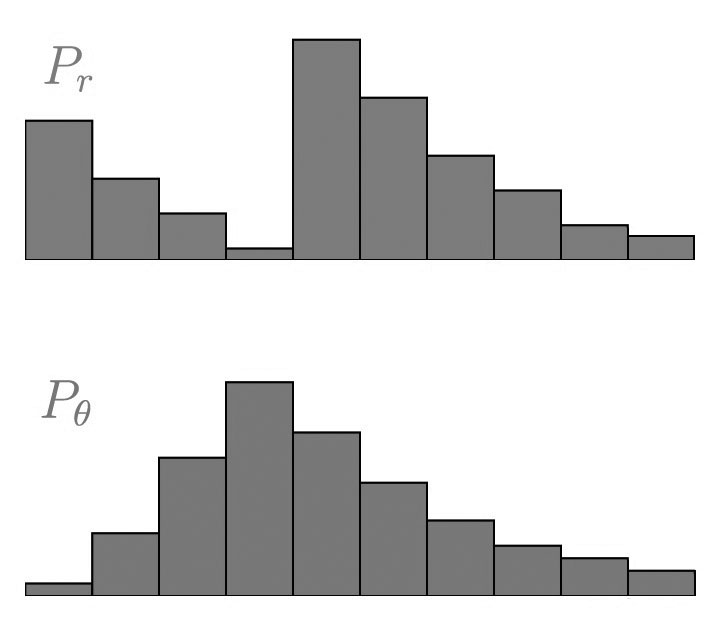
如果我们将分布想象为两个有一定存土量的土堆,每个土堆维度为 $N$,那么 EMD 就是将一个土堆转换为另一个土堆所需的最小总工作量。工作量的定义是单位泥土 的总量乘以它移动的距离。两个离散的土堆分布记作 $P_r$ 和 $P_\theta$ ,以以下两个任意的分布为例。
-
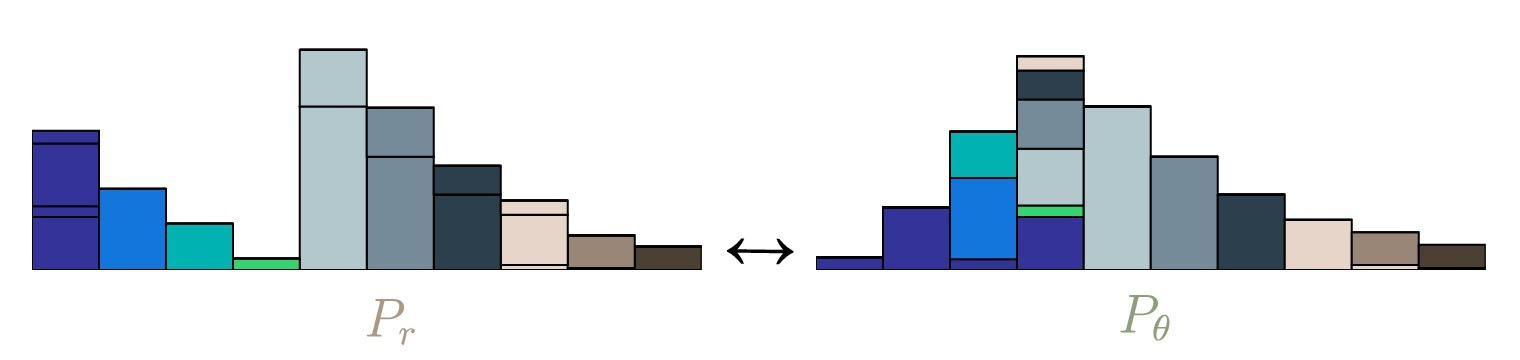
直观理解,土堆 $ P_{r} $ 和 $ P_{\theta} $其中的单个柱条记为,$ P_{r}(x) $ 和 $ P_{\theta}(y) $,每一个 $P_{r}(x) $就是当前 $ x $ 位置土的存量, $ P_{\theta}(x) $ 指的是最终 $ x $ 位置要存放的土量。
- 如果 $ P_{r}(x)>P_{\theta}(x) $:就要将 $x$ 处多余的一部分$ P_{r}(x)-P_{\theta}(x) $土方搬运到别处;
- 如果 $ P_{r}(x)<P_{\theta}(x) $:就要从其他处搬一部分将部分到 $x$ 处,使得 $x$ 处的土方存量为$ P_{r}(x) $。
-
假设联合分布 $ \gamma(x, y) $ 为联合分布,它的边缘分布为前面提到的 $ P_{r} $ 和 $ P_{\theta} $。
-
$ \int \gamma(x, y) d y=P_{r}(x) $ 且 $ \int \gamma(x, y) d x=P_{\theta}(y) $
-
$ P_{r} $ 是原始分布、 $ P_{\theta} $ 是目标分布。$ \gamma(x, y) $ 的含义是,要从 $ x $ 处搬 $ \gamma(x, y) d x $ 这么多的土方到 $ y $ 处。
-
从 $ x $ 处搬运单位土方到 $ y $ 的成本定义为 $ d(x, y) $,常见的成本函数一般可以由 L 范数衍生出来。例如: $ |x-y|{1} 、|x-y|{2} 、|x-y|_{2}^{2} $ 等。
-
Wasserstein 距离就可以定义为:
-
inf ,这里表示下确界,即取最小,也就是说,要从所有的运输方案中,找出总搬运成本
-
$ \int_{x} \int_{y} \gamma(x, y) d(x, y) d x d y $ 最小的方案 $ \gamma(x, y) $ ,这个方案的成本,就是我们要算的$ W\left[P_{r}, P_{\theta}\right] $。
-
用推图来解释就是: 两个土堆的形状确定( $ P_{r} $ 和 $ P_{\theta} $ 确定 )、搬运成本 $ d(x, y) $ 确定,最优的搬运方案 $ \gamma(x, y) $ 下的搬运成本记为两个土堆之间的 Wasserstein 距离。
所以 Wasserstein 距离也被称为"推土机距离"(Earth Mover’s Distance)。
优化问题
- “推土机” 的任务是将分布"搬运"到指定分布,搬走的方法有无数种,但是这不是随便就能搬走的,从一处搬运"土"到另一处需要消耗一定代价,记为成本单价矩阵 $ d(x, y) $,我们的目的是找到成本总和最小的"搬运"方案;
- 实际上距离就是要解决 $ \int_{x} \int_{y} \gamma(x, y) d(x, y) d x d y $ 的最小值,其中 $ d(x, y) $ 是确定的,同时这个最优化需要满足如下约束条件:
- 我们可以将积分的形式写为求和形式:
- 写成内积形式:
其中:
$$ \begin{array}{c}\left.\Gamma=\left[\gamma\left(x_{1}, y_{1}\right), \gamma\left(x_{1}, y_{2}\right), \ldots, \gamma\left(x_{2}, y_{1}\right), \gamma\left(x_{2}, y_{2}\right), \ldots, \gamma\left(x_{n}, y_{1}\right), \gamma\left(x_{n}, y_{2}\right), \ldots, \gamma\left(x_{n}, y_{n}\right)\right)\right]^{T} \\ \left.D=\left[d\left(x_{1}, y_{1}\right), d\left(x_{1}, y_{2}\right), \ldots, d\left(x_{2}, y_{1}\right), d\left(x_{2}, y_{2}\right), \ldots, d\left(x_{n}, y_{1}\right), d\left(x_{n}, y_{2}\right), \ldots, d\left(x_{n}, y_{n}\right)\right)\right]^{T} \end{array} $$- 示例图:
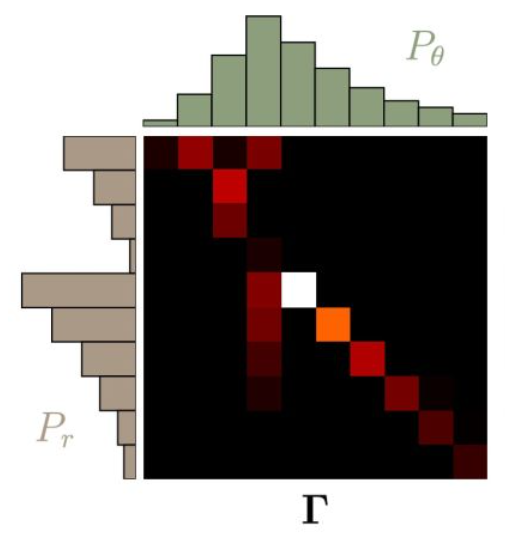 |
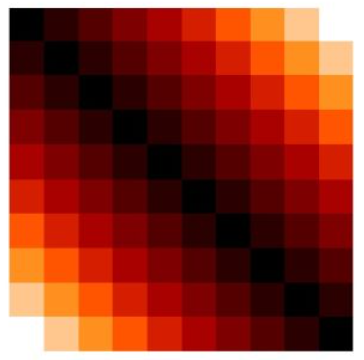 |
- 将 $ P_{r}(x) $ 和 $ P_{\theta}(y) $ 两个向量拼接成一个长的向量 $ b $
- 即,当前已知条件为单价矩阵 $d$,$2N$ 个求和约束条件,同时搬运矩阵值非负,在此种情况下,计算代价最小的搬运方案矩阵 $ \Gamma $
- 也就将问题归化为一个 线性约束条件下的线性函数最小值 的优化问题。
- 最起码可以用 拉格朗日乘数法 解决该问题
参考资料
文章链接:
https://www.zywvvd.com/notes/study/math/distance/emd/emd/
“觉得不错的话,给点打赏吧 ୧(๑•̀⌄•́๑)૭”

微信支付

支付宝支付