线段相交判断

本文最后更新于：2024年8月6日下午

本文记录判断线段是否相交的方法。

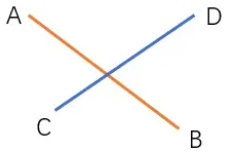
判断线段是否相交

判断线段是否共线

判断 AB 和 CD 向量叉乘是否为 0，如果为 0 则平行，如果 AB 和 AC、 AD 叉乘也为 0 则共线。

随后查看线段是否重叠，分别查看 x, y 是否重叠即可判断。

在不共线情况下判断是否相交

此种情况下线段相交有两种情况

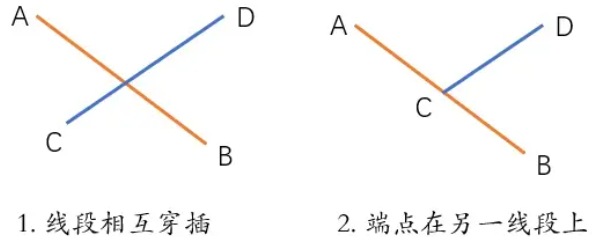
A,B 两点分别在线段 CD 两侧，同时 C, D 两点分别在 AB 线段两侧

$$ \begin{array}{c} (\vec{AC}\times\vec{AB})\cdot(\vec{AD}\times\vec{AB})<0 \\ (\vec{CA}\times\vec{CD})\cdot(\vec{CB}\times\vec{CD})<0 \end{array} $$

第二种情况下由于端点在线段上，所以有一个叉乘为0，因此：

$$ \begin{array}{c} (\overrightarrow{AC}\times\overrightarrow{AB})\cdot(\overrightarrow{AD}\times\overrightarrow{AB})=0 \\(\overrightarrow{CA}\times\overrightarrow{CD})\cdot(\overrightarrow{CB}\times\overrightarrow{CD})=0 \end{array} $$

计算交点

假设交点为$P$,则有$P= A+ \overrightarrow {AB}* t$, $t\in [ 0, 1]$且$P= C+ \overrightarrow {CD}* u$, $u\in [ 0, 1]$ 即 $$ \begin{array}{c} A+ \overrightarrow {AB}* t= C+ \overrightarrow {CD}* u \\ \overrightarrow {AB}* t= \overrightarrow {AC}+ \overrightarrow {CD}* u \end{array} $$ 由于向量自身的叉乘为0，所以上式两边同时叉乘 $\overrightarrow {CD}$ 可得： $$ \vec{CD}\times\vec{AB}*t=\vec{CD}\times\vec{AC} $$ 变形可得： $$ t=\frac{\overrightarrow{CD}\times\overrightarrow{AC}}{\overrightarrow{CD}\times\overrightarrow{AB}},\:t\in[0,1] $$ 同理，两边同时叉乘$\overrightarrow{AB}$可得：$-\overrightarrow{AB}\times\overrightarrow{CD}*u=\overrightarrow{AB}\times\overrightarrow{AC}$ ,所以： $$ u=\frac{\overrightarrow{AB}\times\overrightarrow{AC}}{\overrightarrow{CD}\times\overrightarrow{AB}},\:u\in[0,1] $$