凸集与凸函数

凸函数在优化问题中有着很好的性质，本文记录相关概念。

凸集与凸函数

凸集

• 定义：设集合 $ C \subset \mathbb{R}^{n} $ ，若对 $ \forall x, y \in C $ ，有：
  $$
  \theta x+(1-\theta) y \in C, \theta \in[0,1]
  $$
  则称 $C$ 为 凸集

• 几何意义：若 $ x, y $ 属于凸集 $ C $ 则 $ x $ 与 $ y $ 连线上的所有点都属于凸集 $ C $：

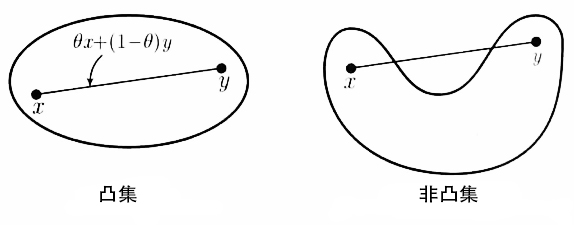
• 性质： 凸集关于加法、数乘和交运算都是封闭的。对于凸集 $ C_{1}, C_{2} \in \mathbb{R}^{n} ， \beta \in \mathbb{R} $ ，则：

  1. $ C_{1}+C_{2}=\left\{x_{1}+x_{2} \mid x_{1} \in C_{1}, x_{2} \in C_{2}\right\} $ 是凸集
  2. $ \beta C_{1}=\left\{\beta x \mid x \in C_{1}\right\} $ 是凸集

  3. $ C_{1} \cap C_{2} $ 是凸集

凸函数

• 定义：设集合 $ C \subset \mathbb{R}^{n} $ 为非空凸集，函数 $ f: C \rightarrow \mathbb{R} $ 。若对 $ \forall x, y \in C $ ，有:

$$
f(\theta x+(1-\theta) y) \leq \theta f(x)+(1-\theta) f(y), \theta \in[0,1]
$$

• 几何意义：凸函数曲线上任意两点连线都在函数曲线之上:

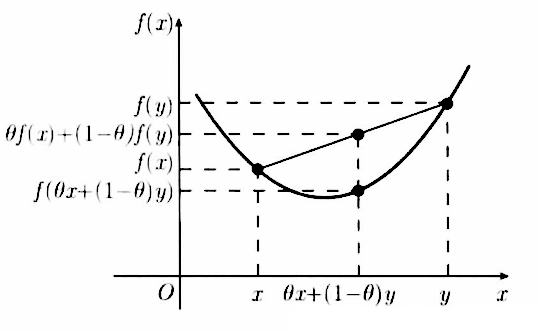
• 判定方法

  1. 一阶判定条件

     设集合 $ C \subset \mathbb{R}^{n} $ 为非空开凸集, 函数 $ f: C \rightarrow \mathbb{R} $ 可微, 则:

     • $f(x)$ 是凸函数当且仅当对$ \forall x, y \in C $ 有：

     $$
     f(y) \geqslant f(x)+g(x)^{\mathrm{T}}(y-x)
     $$

     • $f(x)$ 是严格凸函数当且仅当对$ \forall x, y \in C, x \neq y $有：

     $$
     f(y)>f(x)+g(x)^{\mathrm{T}}(y-x)
     $$

  2. 二阶判定条件

     设集合 $ C \subset \mathbb{R}^{n} $ 为非空开凸集, 函数 $ f: C \rightarrow \mathbb{R} $ 二阶连续可微, 则:

     • $f(x)$ 是凸函数当且仅当对$ \forall x∈C$, Hesse矩阵 $G(x)$ 半正定
     • 若对 $ \forall x∈C$, Hesse矩阵 $G(x)$ 正定，则 $f$ 是严格凸函数。

凸函数判定条件证明

• 凸函数（一元）的定义是： 任意属于定义域的两个自变量 $ x_{1} $ 和 $ x_{2} $ ，且对于任意 $ 0 \leq \theta \leq 1 $ ，如果函数 $ f(\cdot) $ 满足:
  $$
  f\left(\theta x_{1}+(1-\theta) x_{2}\right) \leq \theta f\left(x_{1}\right)+(1-\theta) f\left(x_{2}\right)
  $$
  那么函数 $ f(\cdot) $ 是凸函数。

直观的理解就是函数曲线上任意两点为短点的线段一定在函数曲线的上方。

• 多变量函数可以把自变量写成一个向量 $ \mathbf{x}=\left[x_{1}, x_{2}, \ldots, x_{n}\right]^{T} $ ，同理对于定义域的任意两个 自变量 $ \mathbf{ x } _ { 1 } $ 和 $ \mathbf{x }_ { 2} $ ，以及任意 $ 0 \leq \theta \leq 1 $ ，如果函数 $ f(\cdot) $ 满足:

  $$ f\left(\theta \mathbf{x}_{1}+(1-\theta) \mathbf{x}_{2}\right) \leq \theta f\left(\mathbf{x}_{1}\right)+(1-\theta) f\left(\mathbf{x}_{2}\right) $$

  那么函数 $ f(\cdot) $ 是凸函数。

一阶判定条件充分性证明

• 一阶条件的含义为（以一元函数为例）：对于定义域内任意两个自变量 $ x_{1} $ 和 $ x_{2} $ ，函数 $ f(\cdot) $ 满足则函 $ f\left(x_{2}\right) \geq f\left(x_{1}\right)+f^{\prime}\left(x_{1}\right)\left(x_{2}-x_{1}\right) $ 数 $ f(\cdot) $ 为凸函数。

  

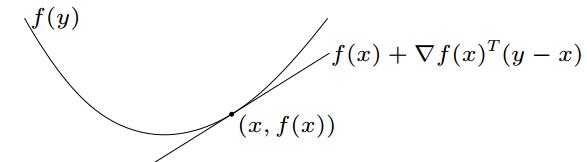
  直观的理解就是函数曲线始终位于任意一点的切线的上方。

• 现在要证明的凸函数有 $f ( x _ { 2 } ) \geq f ( x _ { 1 } ) + f ^ { \prime } ( x _ { 1 } ) ( x _ { 2 } - x _ { 1 } )$ 的性质。

• 假设函数 $f$ 在定义域上是凸函数，那么有：

  $$ \begin{array}{c} { f ( \theta x _ { 1 } + ( 1 - \theta ) x _ { 2 } ) \leq \theta f ( x _ { 1 } ) + ( 1 - \theta ) f ( x _ { 2 } ) } \\ { f ( x _ { 2 } + \theta ( x_1-x _ { 2 } ) ) \leq f ( x _ { 2 } ) + \theta (f ( x _ { 1 } ) - f ( x_2))}\\ { f ( x _ { 2 } + \theta ( x _ { 1 } - x _ { 2 } ) ) - f ( x _ { 2 } ) \leq \theta ( f ( x _ { 1 } ) - f ( x _ { 2 } ) ) } \\ { \frac { f ( x _ { 2 } + \theta ( x _ { 1 } - x _ { 2 } ) ) - f ( x _ { 2 } ) } { \theta } \leq f ( x _ { 1 } ) - f ( x _ { 2 } ) } \end{array} $$

• 变形可以得到:

  $$ f\left(\mathbf{x}_{1}\right) \geq f\left(\mathbf{x}_{2}\right)+\frac{f\left(\mathbf{x}_{2}+\theta\left(\mathbf{x}_{1}-\mathbf{x}_{2}\right)\right)-f\left(\mathbf{x}_{2}\right)}{\theta} $$

• 令 $ g(\theta)=f\left(\mathbf{x}_{2}+\theta\left(\mathbf{x}_{1}-\mathbf{x}_{2}\right)\right) $ ，则 $ g(0)=f\left(\mathbf{x} _ { 2}\right) $ ，那么有
  $$
  f\left(\mathbf{x}_ { 1}\right) \geq f\left(\mathbf{x}_ {2}\right)+\frac{g(\theta)-g(0)}{\theta}
  $$

• 当$\theta$趋近于0时，有:
  $$
  \lim _{\theta \rightarrow 0} \frac{g(\theta)-g(0)}{\theta}=g^{\prime}(0)
  $$

• 这一项也就是函数 $ g(\theta) $ 在 $ \theta=0 $ 处的导数值， $ g(\theta) $ 实际是 $ f(\mathbf{x}) $ 与$ \mathbf{x}=\mathbf{x}_ {2}+\theta\left(\mathbf{x}_ {1}-\mathbf{x}_ {2}\right) $的复合函数，容易求导得:
  $$
  \frac{d g}{d \theta}=\frac{df}{dx}\frac{dx}{d\theta}=\left(\mathbf{x}_ {1}-\mathbf{x}_ {2}\right) \frac{d f\left(\mathbf{x}_ {2}+\theta\left(\mathbf{x}_ {1}-\mathbf{x}_ {2}\right)\right)}{d \mathbf{x}}
  $$

• 由于只要求在$\theta = 0$处的导数值所以容易得

  $$ \left.\frac{d g}{d \theta}\right|_{\theta=0}=\left(\mathbf{x}_ {1}-\mathbf{x}_ {2}\right) \frac{d f\left(\mathbf{x}_ {2}\right)}{d \mathbf{x_ 2}}=\nabla f\left(\mathbf{x}_ {2}\right) \cdot\left(\mathbf{x}_ {1}-\mathbf{x}_ {2}\right) $$

• 代入回不等式即可得到:
  $$
  f\left(\mathbf{x}_ {1}\right) \geq f\left(\mathbf{x}_ {2}\right)+\nabla f\left(\mathbf{x}_ {2}\right) \cdot\left(\mathbf{x}_ {1}-\mathbf{x}_ {2}\right)
  $$

二阶判定条件充分性证明

• 在凸函数的前提下，根据一阶条件可以得到：

$$
f\left(\mathbf{x}_ {1}\right) \geq f\left(\mathbf{x}_ {2}\right)+\nabla f\left(\mathbf{x}_ {2}\right) \cdot\left(\mathbf{x}_ {1}-\mathbf{x}_ {2}\right)
$$

• 将 $f$ 在任一点 $x_0$ 泰勒展开：
  $$
  f\left(\mathbf{x}_ {0}+t \mathbf{d}\right)=f\left(\mathbf{x}_ {0}\right)+t \nabla f\left(\mathbf{x}_ {0}\right) \mathbf{d}+\frac{t^{2}}{2} \mathbf{d}^{T} \mathbf{H d}+o\left(t^{2}\right)
  $$

• 其中 $ t$ 为长度（标量），$d$ 为任意向量

• 根据以上两个公式可得：

  $$ \begin{array}{c} \frac{t^{2}}{2} \mathbf{d}^{T} \mathbf{H d}+o\left(t^{2}\right) \geq 0 \\ \mathbf{d}^{T} \mathbf{H d}+\frac{2 o\left(t^{2}\right)}{t^2} \geq 0 \end{array} $$

• 该不等式在 $t \to 0 $ 时仍然成立，而 $t \to 0 $ 时有：

$$
\lim _{t \rightarrow 0} \frac{o\left(t^ {2}\right)}{t^ {2}}=0
$$

• 因此有：

$$
\mathbf{d}^{T} \mathbf{H d} \geq 0
$$

• 即 Hessian 矩阵 $\mathbf{H}$ 必须半正定。

参考资料

• https://blog.csdn.net/wxc971231/article/details/115275103
• https://www.zhihu.com/question/40181086/answer/693868441

文章链接：
https://www.zywvvd.com/notes/study/math/convex-func/convex-func/