异常检测 SVDD 算法

机器学习中的异常检测在很多场景有重要应用，本文记录 SVDD 算法。

简介

支持向量数据描述 SVDD（Support Vector Data Description，SVDD）是一种单值分类算法，能够实现目标样本和非目标样本的区分，通常应用于异常检测、入侵检测等领域。

• 论文链接

单分类问题

• 单分类问题的目的并不时将不同类别的数据区分开来，而是对某个类别的数据生成一个描述（description），可以理解为是样本空间中的一个区域，当某个样本落在这个区域外，我们就认为该样本不属于这个类别。

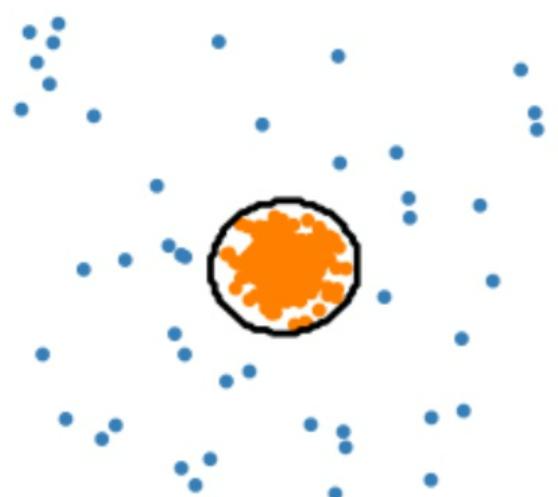
SVDD 思想

SVDD 的思路是寻找一个尽可能小的高维球体，将训练数据容纳进去，那么在预测数据时，认为在球体之外的数据为异常数据。

算法原理

原始问题

• 假设我们有 $m$ 个样本点，分别为 $x(1),x(2),\cdots ,x(m)$ 。
• 我们假设这些样本点分布在一个球心为 $a$ ，半径为 $R$ 的球中。那么样本 $x(i)$ 满足

$$(x^{(i)}-a{)}^T(x^{(i)}-a)\le R^2$$

• 为了允许部分样本不在这个球中，我们引入松弛变量：

$${(x^{(i)}-a)}^T(x^{(i)}-a)\le R^2+{\xi }_i,\xi \ge 0$$

• 我们的目标是最小球的半径 $R$ 和松弛变量的值，于是目标函数:

$$\begin{array}{c}\underset{a,\xi ,R}{min}{R}^2+C\sum _{i=1}^m{\xi }_i\\ \text{ s.t. }{(x^{(i)}-a)}^T(x^{(i)}-a)\le R^2+{\xi }_i,\\ {\xi }_i\ge 0,i=1,2,\cdots ,m.\end{array}$$

其中，$C>0$ 是惩罚参数，由人工设置。

• 写成拉格朗日方程：

$$\begin{array}{rl}L(R,a,\alpha ,\xi ,\gamma )=& R^2+C\sum _{i=1}^m{\xi }_i-\sum _{i=1}^m{\alpha }_i(R^2+{\xi }_i-(x^{(i{)}^T}{x}^{(i)}-2a^T{x}^{(i)}+a^2))-\sum _{i=1}^m{\gamma }_i{\xi }_i.\end{array}$$

• 其中， ${\alpha }_i\ge 0,{\gamma }_i\ge 0$ 是拉格朗日乘子。

• 此时事实上涉及到了需要用 $\alpha$ 选择支持向量了，但是此时其他参数都还没有确定，那么确定那个样本作为支持向量更是无从谈起，因此原始问题：

$$\underset{R,a,\xi }{min}\underset{\alpha ,\gamma ;\alpha \ge 0}{max}L(R,a,\alpha ,\xi ,\gamma )$$

​ 无法求解，幸运的是该问题总体是凸优化问题，对偶问题与原问题等价，我们尝试求解对偶问题

对偶问题

• 对偶问题：

$$\underset{\alpha ,\gamma ;\alpha \ge 0}{max}\underset{R,a,\xi }{min}L(R,a,\alpha ,\xi ,\gamma )$$

• 令拉格朗日函数对 $R,a,{\xi }_i$ 的偏导为 0，得到:

$$\begin{array}{c}\sum _{i=1}^m{\alpha }_i=1\\ a=\sum _{i=1}^m{\alpha }_i{x}^{(i)}\\ C-{\alpha }_i-{\gamma }_i=0\end{array}$$

• 我们可以将 ${\alpha }_i$ 看作样本 $x^{(i)}$ 的权重。上式表明所有样本的权重之和为1，而球心 $a$ 是所有样本的加权和。将上式带入到拉格朗日函数中:

$$\begin{array}{c}\underset{\alpha }{max}L(\alpha )=\sum _{i=1}^m{\alpha }_i{x}^{(i{)}^T}{x}^{(i)}-\sum _{i=1}^m\sum _{j=1}^m{\alpha }_i{\alpha }_j{x}^{(i{)}^T}{x}^{(j)}\\ s.t.0\le {\alpha }_i\le C\\ \sum _{i=1}^m{\alpha }_i=1,i=1,2,\cdots ,m.\end{array}$$

• 当通过求解对偶问题得到 ${\alpha }_i$ 后，可以通过 $a=\sum _{i=1}^m{\alpha }_i{x}^{(i)}$ 计算球心 $a$ 。
• 半径 $R$，则可以通过计算球心与支持向量（ ${\alpha }_i<C$ ）之间的距离得到。当 ${\alpha }_i=C$ 时，意味着样本$x^{(i)}$ 位于球的外面。

判断新样本是否为异常点

• 对于一个新的样本点 $z$ ，如果它满足下式，那么我们认为它是一个异常点。

$$(z-a{)}^T(z-a)>R^2$$

• 展开上式，得:

$$z^{T}z-2\sum _{i=1}^m{\alpha }_i{z}^T{x}^{(i)}+\sum _{i=1}^m\sum _{j=1}^m{\alpha }_i{\alpha }_j{x}^{(i{)}^T}{x}^{(j)}>R^2$$

引入核函数

正常情况下，数据并不会呈现球状分布，因此有必要使用核函数的方法提高模型的表达能力。

• 只需将 $K(x^{(i)},x^{(j)})$ 替换 $ x^{(i){T}} x^{(j)} $ 即可。

• 在训练前通过变换函数$\Phi :x\to F$ 将数据从原始空间映射到新特征空间, 然后在新特征空间中导找一个体积最小的超球体, SVDD 要解决的优化问题变为:

$$\begin{array}{c}\underset{\mathbf{a},R,\xi }{min}{R}^2+C\sum _{i=1}^n{\xi }_i\\ s.t.{\Vert \mathrm{\Phi }\left({\mathbf{x}}_i\right)-\mathbf{a}\Vert }^2\le R^2+{\xi }_i,\\ {\xi }_i\ge 0,\mathrm{\forall }i=1,2,\cdots ,n\end{array}$$

• 那么对偶问题会变为

$$\begin{array}{c}\underset{{\alpha }_i}{min}\sum _{i=1}^n\sum _{j=1}^n{\alpha }_i{\alpha }_{j}K({\mathbf{x}}_i,{\mathbf{x}}_j)-\sum _{i=1}^n{\alpha }_{i}K({\mathbf{x}}_i,{\mathbf{x}}_i)\\ s.t.0\le {\alpha }_i\le C,\\ \sum _{i=1}^n{\alpha }_i=1\end{array}$$

• 求解该对偶问题后，可以获取所有样本对应的拉格朗日系数。
• 拉格朗日系数满足 $0<{\alpha }_i<C$ 的样本称为支持向量，用 ${\mathbf{x}}_{\mathbf{v}}$ 表示，那么球心和半径的公式为：

$$\mathbf{a}=\sum _{i=1}^n{\alpha }_i\mathrm{\Phi }\left({\mathbf{x}}_i\right)$$ $$R=\sqrt{K({\mathbf{x}}_v,{\mathbf{x}}_v)-2\sum _{i=1}^n{\alpha }_{i}K({\mathbf{x}}_v,{\mathbf{x}}_i)+\sum _{i=1}^n\sum _{j=1}^n{\alpha }_i{\alpha }_{j}K({\mathbf{x}}_i,{\mathbf{x}}_j)}$$

多项式核

• 多项式核函数的表达式如下:

$$\mathcal{K}\left(x^{(i{)}^T}{x}^{(j)}\right)=(x^{(i{)}^T}{x}^{(j)}+1{)}^d$$

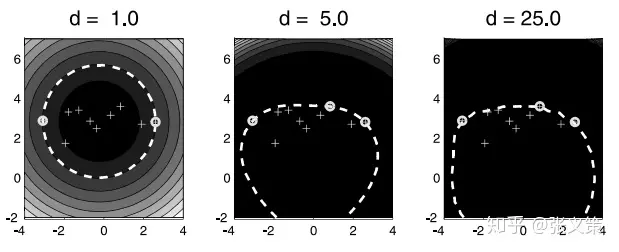
• 如下图所示，多项式核实际上不太适合 SVDD。特别是当 $d$ 取值非常大的时候。

img

高斯核

• 高斯核函数的表达式如下

$$\mathcal{K}\left(x^{(i{)}^T}{x}^{(j)}\right)=\exp (\frac{-{(x^{(i)}-x^{(j)})}^2}{s^2})$$

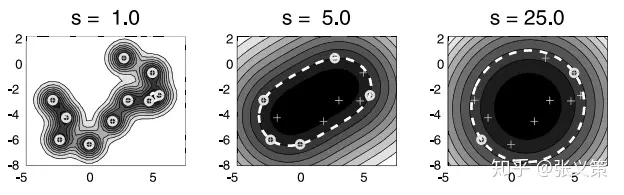
• 如下图，相比于多项式核函数，高斯核函数的结果就合理多了。可以看到模型的复杂程度随着 $s$ 的增大而减小。

img

原始论文

参考资料

• Tax D M J, Duin R P W. Support vector domain description[J]. Pattern recognition letters, 1999, 20(11-13): 1191-1199.
• https://zhuanlan.zhihu.com/p/65617987
• https://dreamhomes.top/posts/202105081146/
• https://blog.csdn.net/OrthocenterChocolate/article/details/40592403

文章链接：
https://www.zywvvd.com/notes/study/machine-learning/one-class/svdd/svdd/