SVM 中的核函数 (kernel function)

SVM 在实际应用时往往会用到核函数，可以用很小的计算代价达到提升特征维度的效果，本文记录相关内容。

核函数

定义

• 函数 $\Phi$ 是一个从低维特征空间到高维特征空间的一个映射，那么如果存在函数 $K(x,z)$, 对于任意的低维特征向量 $x$ 和 $z$，都有：

$$
\mathrm{K}(x, z)=\Phi(x) \bullet \Phi(z)
$$

​ 则称函数 $K(x,z)$ 为核函数 (kernel function), $\Phi(x)$ 为映射函数，$\Phi(x) \bullet \Phi(z)$ 为 $x,y$ 映射到特征空间上的内积。

• 本质： 核函数是一个低维的计算结果，并没有采用低维到高维的映射。只不过核函数低维运算的结果等价于映射到高维时向量点积的值。

意义

• 其实在 SVM 的计算过程中，求解部分已经很漂亮地推导出来了，为何还要引入核函数呢。
• 其目的是可以使得有时在低维空间难以找到划分超平面的问题在高维空间中得到缓解：

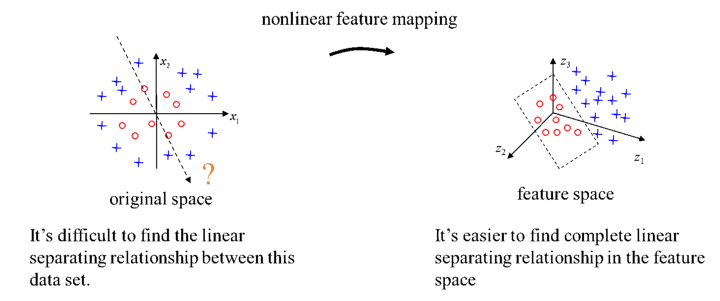
• 至于为何其内核是内积的形式就要聊一聊 SVM 中内积运算的部分。

SVM 中的内积运算

SVM 的求解和推断过程均可以表示为数据的内积运算，因此核函数替换内积后完全不影响结果，但是会显著提升高维特征的 SVM 运算速度。

求解过程

• 根据我们之前对 SVM 的推导过程 ，我们得到了带有核函数的优化目标拉格朗日方程：

$$ \begin{array}{c} L(w, b, \alpha)=\frac{1}{2}\|w\|^{2}-\sum_{i=1}^{n} \alpha_{i}\left(y_{i}\left(w^{T} \cdot \Phi\left(x_{i}\right)+b\right)-1\right) \\ s.t. y_{i}\left(w^{T} \cdot \Phi\left(x_{i}\right)+b\right) \geq 1 \end{array} $$

• 对对偶问题求解之后对 $w$ 和 $b$ 求偏导等于零得到的结果：

$$ \begin{array}{l} \frac{\partial L}{\partial w}=0 \Rightarrow w=\sum_{i=1}^{n} \alpha_{i} y_{i} \Phi\left(x_{n}\right) \\ \frac{\partial L}{\partial b}=0 \Rightarrow 0=\sum_{i=1}^{n} \alpha_{i} y_{i} \end{array} $$

• 最终 SVM 转为一个带约束的极小值优化问题：

$$ \begin{array}{l} \min _{\alpha} \frac{1}{2} \sum_{i=1}^{n} \sum_{j=1}^{n} \alpha_{i} \alpha_{j} y_{i} y_{j}\left(\Phi\left(x_{i}\right) \cdot \Phi\left(x_{j}\right)\right)-\sum_{i=1}^{n} \alpha_{i}\\ s.t. \sum_{i=1}^{n} \alpha_{i} y_{i}=0 , \alpha_{i} \geq 0 \end{array} $$

• 之后需要用 SMO 算法 求解 $\alpha$ 这其中所有 $x$ 相关的计算均为数据之间的内积运算，因此如果我们设计好了核函数 $K$，那么我们将所有的 $\left(\Phi\left(x_{i}\right) \cdot \Phi\left(x_{j}\right)\right)$ 换为 $K(x_i, x_j)$，不影响后续 $\alpha$ 的求解
• 也就是说： 核函数可以嵌入 SVM 的求解过程，不影响求解的过程，并且在求解时就已经避免了 $\Phi(x)$ 的高维运算；

推断过程

• 原始的分类平面为：

$$
w^{T} x+b=0
$$

• 那么最终的分类函数为：

$$
f(x)=\operatorname{sign}\left(w^{T} x+b\right)
$$

• 根据 SVM 的推导，有结论：

$$
w=\sum_{i=1}^{n} \alpha_{i} y_{i} x_{i}
$$

• 假设 $x_j$ 为支持向量 ，$b$ 为：

$$
b=y_j-w^Tx_j
$$

• 带入分类函数：

$$ \begin{aligned} f(x) &=w^{T} x+b \\ &=(\sum_{i=1}^{n} \alpha_{i} y_{i} x_{i})^{T} x+y_j-(\sum_{i=1}^{n} \alpha_{i} y_{i} x_{i})^{T}x_j\\ &=\sum_{i=1}^{n} \alpha_{i} y_{i}\left\langle x_{i}, x\right\rangle+y_j-\sum_{i=1}^{n} \alpha_{i} y_{i} \langle x_{i},x_j \rangle \end{aligned} $$

• 如果此时对原始数据，引入核函数：

$$
f(x)=\sum_{i=1}^{n} \alpha_{i} y_{i} K(x_{i},x)+y_j-\sum_{i=1}^{n} \alpha_{i} y_{i} K(x_{i},x_j)
$$

• 也就是说原始分类函数完全可以用核函数运算来表示
• 而且其中 $b$ 的运算结果是一个常数，算完放在那用就好了
• $w$ 的计算看起来有求和符号需要对所有训练数据求和，但是事实上仅有支持向量的 $\alpha$ 非零，仅需极小的复杂度就可以完成对数据的推断。

核函数条件

我们知道了什么是核函数，看到了核函数在 SVM 中的巧妙运用，也就是只要定义好核函数，求解推断一切都可以包办，但什么样的函数可以成为核函数呢。

• 假设一个函数 $K(x,y)$，我们想要确定是否有某个映射函数 $\Phi$ 对应 $K$ ，使得 $\mathrm{K}(x, z)=\Phi(x) \bullet \Phi(z)$，也就是判定这个 Kernel 函数是否可用 (Valid)

必要条件

• 根据 SVM 的计算需求，由于内积运算是可交换的，那么 $K$ 也必须可交换，即：

$$
K(x,y)=K(y,x)
$$

• 定义矩阵 $M$ 为 （在 SVM 中成为核矩阵）:

$$ \begin{array}{c} M &=&\left[\begin{array}{cccc}\boldsymbol{\Phi}\left(\mathbf{x}_{1}\right)^{T} \boldsymbol{\Phi}\left(\mathbf{x}_{1}\right) & \boldsymbol{\Phi}\left(\mathbf{x}_{1}\right)^{T} \boldsymbol{\Phi}\left(\mathbf{x}_{2}\right) & \ldots & \boldsymbol{\Phi}\left(\mathbf{x}_{1}\right)^{T} \boldsymbol{\Phi}\left(\mathbf{x}_{N}\right) \\ \boldsymbol{\Phi}\left(\mathbf{x}_{2}\right)^{T} \boldsymbol{\Phi}\left(\mathbf{x}_{1}\right) & \boldsymbol{\Phi}\left(\mathbf{x}_{2}\right)^{T} \boldsymbol{\Phi}\left(\mathbf{x}_{2}\right) & \ldots & \boldsymbol{\Phi}\left(\mathbf{x}_{2}\right)^{T} \boldsymbol{\Phi}\left(\mathbf{x}_{N}\right) \\ \Phi\left(\mathbf{x}_{N}\right)^{T} \boldsymbol{\Phi}\left(\mathbf{x}_{1}\right) & \boldsymbol{\Phi}\left(\mathbf{x}_{N}\right)^{T} \boldsymbol{\Phi}\left(\mathbf{x}_{2}\right) & \ldots & \boldsymbol{\Phi}\left(\mathbf{x}_{N}\right)^{T} \boldsymbol{\Phi}\left(\mathbf{x}_{N}\right)\end{array}\right] \\ &=&\left[\begin{array}{lllll}\mathbf{z}_{1} & \mathbf{z}_{2} & \ldots & \mathbf{z}_{N}\end{array}\right]^{T}\left[\begin{array}{llll}\mathbf{z}_{1} & \mathbf{z}_{2} & \ldots & \mathbf{z}_{N}\end{array}\right] \end{array} $$

• 其中 $\mathbf{z}_{i} = \boldsymbol{\Phi}\left(\mathbf{x}_{i}\right)$，那么 $M$ 可以看做是一个整合成平方形式的二项式的二次型参数矩阵，因此该矩阵必定是半正定的
• 总结一下两个核函数 $K$ 的两个必要条件：

1. 可交换
2. 对于当前数据的核矩阵半正定

充分条件

• 以上两条必要条件被前辈数学家证明也是充分条件…
• 那么上述两个要求 $K$ 的条件即是该核函数可用的充要条件

常用核函数

线性核函数

$$
K(x,y)=\langle x,y\rangle
$$

多项式核函数

$$
K(x,y)=(\langle x,y\rangle+c)^d
$$

高斯核函数

$$ K(x, y)=e^{-\frac{\|x-y\|^{2}}{2 \sigma^{2}}} $$

参考资料

• https://chih-sheng-huang821.medium.com/機器學習-kernel-函數-47c94095171
• https://zhuanlan.zhihu.com/p/261061617
• https://www.jianshu.com/p/028d1883ad93
• https://www.zywvvd.com/notes/study/machine-learning/about-svm/svm-summarize/svm-summarize/
• http://t.zoukankan.com/JZ-Ser-p-7479757.html

文章链接：
https://www.zywvvd.com/notes/study/machine-learning/about-svm/svm-kernel/svm-kernel/