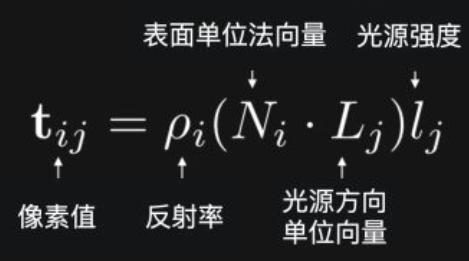Photometric Stereo 光度立体法三维重建

光度立体法，可以利用多张不同光照的相同机位相机拍摄的图像建模计算出物体表面深度、法向量，本文记录基础理论。

光度立体法

光度立体法，即Photometric Stereo, 最早是由当时在MIT的人工智能实验室的Robert J. Woodham教授在1978年左右提出。他在1979年的论文《Photometric stereo: A reflectance map technique for determining surface orientation from image intensity》，以及1980年的论文《Photometric Method for Determining Surface Orientation from Multiple Images》中比较系统的阐述了整套理论框架。

实现思路

• 当相机和目标物体相对位置固定不变时，使用不同方向的光源照射同一目标物体，相机可以拍摄到目标物体带有不同明暗分布的图像，再通过求解基于朗伯反射原理的反射方程组，求解目标表面的法向分布或者深度图。
• 为图中像素值产生的过程建立和物体表面属性精确的假设模型，求解低秩矩阵解得物体属性。

基本假设

基础的光度立体法对成像提出三个基本假设

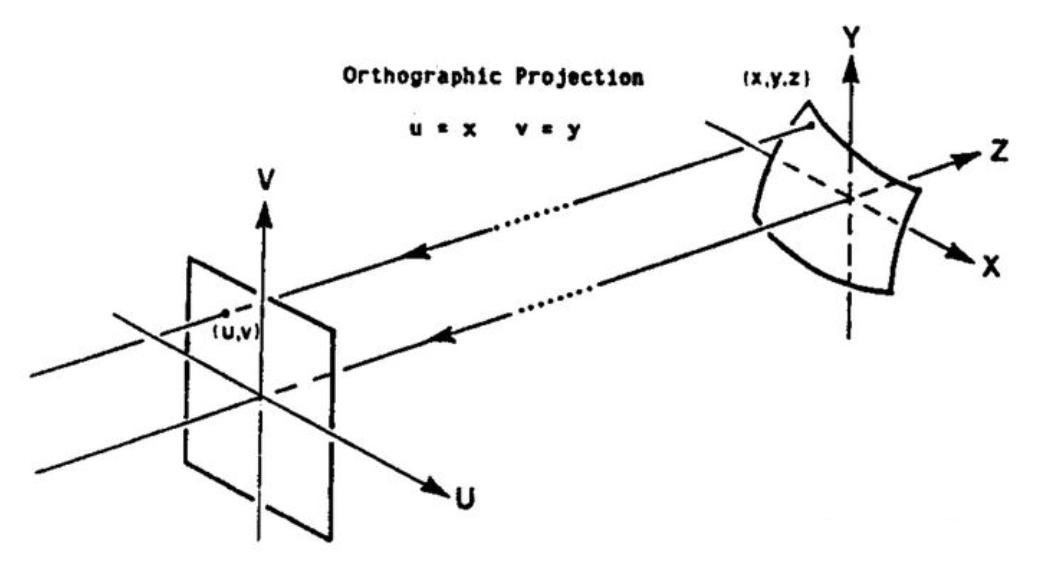
正交投影

图像的 $u,v$ 坐标直接对应物体的 $x,y$ 坐标值

入射光由远处的单一点光源发出

• 光线照到物体表面每一点的光的方向一致，强度一致

物体表面具有朗伯（lambertian）反射特性

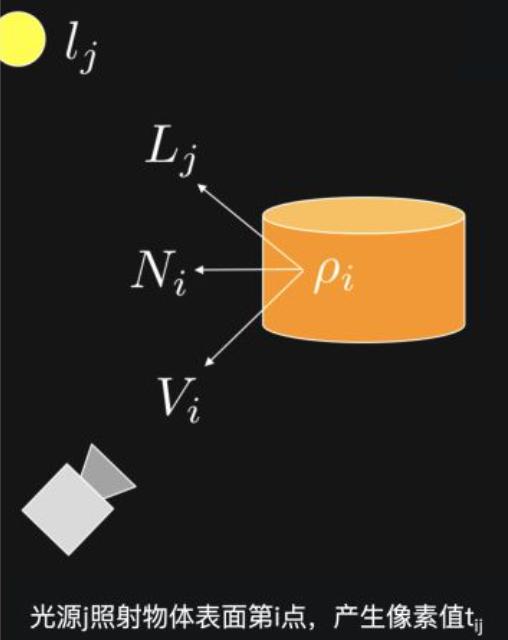
• 相机接收到的光线（像素值）与物体表面属性、表面法向量、入射光角度和强度维持一种特定的关系

• 满足以下漫反射公式

$$t_{ij}={\rho }_i(N_i·L_i)l_j$$

其中各变量含义：

求解物体表面深度

• 将反射公式表示成图像的像素值，公式变为

$$I_{x,y}^i={\rho }_{x,y}{L}_i{\mathbf{L}}_{\mathbf{i}}\cdot {\mathbf{N}}_{x,y}$$

• $i$ 表示第 $i$ 个光源，将$L_i$合并入$\rho$，用 $k_{x,y}$ 表示（$k_{x,y}=\rho L_i$），因此可以假设$L_i$为1，当前公式为：

$$I_{x,y}^i=k_{x,y}{\mathbf{N}}_{x,y}·{\mathbf{L}}_{\mathbf{i}}$$

• 对于图像中特定像素$(x,y)$：

$$\begin{array}{c}{I}_{x,y}^1=k_{x,y}{\mathbf{N}}_{x,y}·{\mathbf{L}}_{\mathbf{1}}\\ I_{x,y}^2=k_{x,y}{\mathbf{N}}_{x,y}·{\mathbf{L}}_{\mathbf{2}}\\ ...\\ I_{x,y}^n=k_{x,y}{\mathbf{N}}_{x,y}·{\mathbf{L}}_{\mathbf{n}}\end{array}$$

• 将 $k$ 合并入 $\mathbf{N}$，用 $\mathbf{G}$ 表示，$\mathbf{G}=k\mathbf{N}$，对于第 $i$ 个光源 $(x,y)$像素：

$$I_{x,y}^i={\mathbf{G}}_{x,y}{\mathbf{L}}_i$$

• 多个光源组成方程组（至少需要三个）

$$\begin{array}{c}{I}_{x,y}^1={\mathbf{G}}_{x,y}{\mathbf{L}}_{\mathbf{1}}\\ I_{x,y}^2={\mathbf{G}}_{x,y}{\mathbf{L}}_{\mathbf{2}}\\ ...\\ I_{x,y}^n={\mathbf{G}}_{x,y}{\mathbf{L}}_{\mathbf{n}}\end{array}$$

• 表示为矩阵：

$$\begin{array}{rl}[L]G& =[I]\\ L^{T}LG& =L^{T}I\\ G& ={\left(L^{T}L\right)}^{-1}{L}^{T}I\end{array}$$

• 因此有：

$$\begin{array}{rl}{k}_d& =\Vert G\Vert \\ N& =G/k_d\end{array}$$

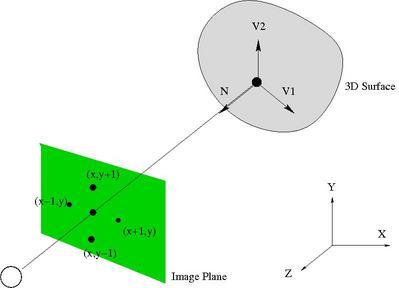
• 物体表面沿着 $x,y$ 方向的导数与法线方向正交

• $x$方向梯度向量$V1$ 为：

$$V_1=(x+1,y,z_{x+1,y})-(x,y,z_{x,y})=(1,0,z_{x+1,y}-z_{x,y})$$

• $V1$与$N$垂直：

$$\begin{array}{rl}N.V_1& =0\\ (n_x,n_y,n_z)\cdot (1,0,z_{x+1,y}-z_{x,y})& =0\\ n_x+n_z(z_{x+1,y}-z_{x,y})& =0\end{array}$$

• 同理 $V2$：

$$\begin{array}{rl}{V}_2& =(x,y+1,z_{x,y+1})-(x,y,z_{x,y})\\ & =(0,1,z_{x,y+1}-z_{x,y})\end{array}$$

• $V2$与 $N$ 垂直：

$$\begin{array}{rl}N.V_2& =0\\ (n_x,n_y,n_z)\cdot (0,1,z_{x,y+1}-z_{x,y})& =0\\ n_y+n_z(z_{x,y+1}-z_{x,y})& =0\end{array}$$

• 如果有像素由于边界问题，有些像素需要使用其他方向的梯度：

$$\begin{array}{rl}-n_x+n_z(z_{x-1,y}-z_{x,y})& =0\\ -n_y+n_z(z_{x,y-1}-z_{x,y})& =0\end{array}$$

• 我们还以$V1,V2$ 为例，整理可得：

$$\begin{array}{r}{z}_{x+1,y}-z_{x,y}=-\frac{{\mathit{n}}_x^{x,y}}{{\mathit{n}}_z^{x,y}}\\ z_{x,y+1}-z_{x,y}=-\frac{{\mathit{n}}_y^{x,y}}{{\mathit{n}}_z^{x,y}}\end{array}$$

• 假设求解的点有 $M$ 个点，那么需要求解的 $z$ 有 $M$ 个，$n$ 的比值 $M$ 个，那么可以列出 $2M\ast M$ 维系数矩阵，并有等式:

$$\left[\begin{array}{cccccc}⋮& ⋮& ⋮& ⋮& ⋮& ⋮\\ \cdots & -1& 1& \cdots & \cdots & \cdots \\ ⋮& ⋮& ⋮& ⋮& ⋮& ⋮\\ ⋮& ⋮& ⋮& ⋮& ⋮& ⋮\\ \cdots & -1& \cdots & \cdots & 1& \cdots \\ ⋮& ⋮& ⋮& ⋮& ⋮& ⋮\end{array}\right]\left[\begin{array}{c}⋮\\ z_{a,b}\\ z_{a,b+1}\\ ⋮\\ z_{a+1,b}\\ ⋮\end{array}\right]=\left[\begin{array}{c}⋮\\ -\frac{{\mathit{n}}_x^{a,b}}{{\mathit{n}}_z^{a,b}}\\ -\frac{{\mathit{n}}_x^{a,b+1}}{{\mathit{n}}_z^{a,b+1}}\\ ⋮\\ -\frac{{\mathit{n}}_x^{a+1,b}}{{\mathit{n}}_z^{a+1,b}}\\ ⋮\end{array}\right]$$

• 求解这个稀疏线性方程组，便可以得到物体的深度。

相关项目

• https://github.com/Robin-WZQ/Photometric-Stereo

• 效果示例

• https://github.com/yasumat/RobustPhotometricStereo

参考资料

• https://blog.csdn.net/SZU_Kwong/article/details/112757354

• https://www.jianshu.com/p/c8391a848425

• https://zhuanlan.zhihu.com/p/205778332

• https://pages.cs.wisc.edu/~csverma/CS766_09/Stereo/stereo.html

• https://www.zhihu.com/question/388447602/answer/1200616778

• https://blog.csdn.net/SZU_Kwong?type=blog

• https://xw.qq.com/cmsid/20220218A0A1Y900

文章链接：
https://www.zywvvd.com/notes/study/image-processing/photometric-stereo/basic/