本文最后更新于：2024年1月14日 晚上

OpenCV 自带大量矩阵处理函数，本文记录相关内容。

简介

  • OpenCV 矩阵类的成员函数可以进行很多基本的矩阵操作，本文基于 《学习 OpenCV3 》中第五章的内容整理 Python OpenCV 矩阵操作函数。

内容列表

序号 函数 描述
1 cv2.exp() 实现矩阵的逐元素求指数幂
2 cv2.flip() 绕选定的轴翻转矩阵
3 cv2.gemm() 实现广义矩阵乘法
4 cv2.idct() 计算矩阵的离散余弦逆变换
5 cv2.idft() 计算矩阵的离散傅里叶逆变换
6 cv2.inRange() 测试矩阵的元素是否在两个其他矩阵的值之间
7 cv2.invert() 求方阵的逆
8 cv2.log() 计算矩阵逐元素的自然对数
9 cv2.LUT() 将矩阵转换为查找表的索引
10 cv2.magnitude() 计算二维向量的幅度
11 cv2.Mahalanobis() 计算两个向量之间的马氏距离
12 cv2.max() 计算两个矩阵逐元素的最大值
13 cv2.mean() 计算矩阵元素的平均值
14 cv2.meanStdDev() 计算矩阵元素的均值和标准差
15 cv2.merge() 将多个单通道矩阵合并成一个多通道矩阵
16 cv2.min() 计算两个矩阵逐元素的最小值
17 cv2.minMaxLoc() 在矩阵中寻找最小值和最大值
18 cv2.mixChannels() 打乱从输入矩阵到输出矩阵的通道
19 cv2.multiply() 计算两个矩阵的逐元素乘积
20 cv2.mulTransposed() 计算矩阵和矩阵的转置的乘积
21 cv2.norm() 计算矩阵/矩阵差的范数
22 cv2.normalize() 将矩阵中的元素标准化到某一数值内
23 cv2.perspectiveTransform() 实现一系列向量的透视矩阵变换

矩阵操作

0. 基础引用

  • 之后对上述函数进行示例演示
  • 所有代码默认引用如下包
1
2
3
4
import cv2
import numpy as np
import mtutils as mt
from mtutils import PIS
  • 示例图片 img1.jpg 和 img2.jpg

  • 查看 opencv 某函数 func 文档可以运行：
1
print(cv2.<func>.__doc__)

1. cv2.exp()

实现矩阵的逐元素求 e 为底的指数幂

1
2
3
4
5
6
7
8
vector = np.ones([3, 3]) + 1
res = cv2.exp(vector)

-->
res
array([[7.3890561, 7.3890561, 7.3890561],
       [7.3890561, 7.3890561, 7.3890561],
       [7.3890561, 7.3890561, 7.3890561]])

相当于 $e^2$

2. cv2.flip()

绕选定的轴翻转矩阵

  • 函数使用
1
cv2.flip(src, flipCode=0)

  • flipCode

    • 该函数将图像绕着x轴或y轴或者同时绕着x轴和y轴翻转。默认情况下，flipCode被设置为 0,图像绕 x 轴翻转。

    • 如果flipCode被设置为大于0的数(例如，+1)，图像会绕y轴翻转，如果被设置为一个负数(例如，-1)，图像将围绕x轴和y轴翻转。

  • 示例代码

1
2
3
4
5
image_1 = mt.cv_rgb_imread('img1.jpg')
y_flip = cv2.flip(image_1, flipCode=1)
x_flip = cv2.flip(image_1, flipCode=0)
xy_flip = cv2.flip(image_1, flipCode=-1)
PIS([image_1,'origin'], [y_flip, 'flipCode 1 y flip'], [x_flip, 'flipCode 0 x flip'], [xy_flip, 'flipCode -1 xy flip'])

3. cv2.gemm()

实现广义矩阵乘法,实现以下计算

其中src1,src2和src3是矩阵，alpha 和 beta 是数值系数，op() 是对所含矩阵的可选转置操作。转置是由可选参数flags来控制的，它的值可以是0或者是cv2.GEMM_1_T,cv2.GEMM_2_T和cv2.GEMM_3_T（每一个标志都与一个矩阵转置相对应）的任意组合（通过布尔 0R 操作）。

$$ D=\alpha \cdot o p\left(\operatorname{src}_{1}\right){·} \operatorname{op}\left(s r c_{2}\right)+\beta \cdot o p\left(\operatorname{src}_{3}\right) $$
  • 函数使用
1
cv2.gemm(src1, src2, alpha, src3, beta, flags)
  • 示例代码
1
2
3
4
5
6
7
8
9
10
11
12
13
mat_1 = np.ones([3,5])
mat_2 = np.ones([3,5])
mat_3 = np.ones([5,5])

res = cv2.gemm(mat_1, mat_2, 2, mat_3, 3, flags=cv2.GEMM_1_T)

-->
res
array([[9., 9., 9., 9., 9.],
       [9., 9., 9., 9., 9.],
       [9., 9., 9., 9., 9.],
       [9., 9., 9., 9., 9.],
       [9., 9., 9., 9., 9.]])

4. cv2.idct()

计算矩阵的离散余弦逆变换 ,就是 cv2.dct(src, flags=cv2.DCT_INVERSE) 的简写

1
2
3
4
5
6
7
8
image = mt.cv_rgb_imread('img1.jpg')
image = mt.image_resize(image, [300, 300]).astype('float32')
image = mt.to_gray_image(image)

dct_res = cv2.dct(image)

res = cv2.idct(dct_res)
PIS(res)

5. cv2.idft()

计算矩阵的离散傅里叶逆变换，cv2.idft()只是离散傅里叶逆变换的一个方便的简写。对cv2.idft()的调用实际上相当
于调用带参数的cv2.dft(src, flags=cv2.DCT_INVERSE)

1
2
3
4
5
6
7
image = mt.cv_rgb_imread('img1.jpg')
image = mt.image_resize(image, [300, 300]).astype('float32')
image = mt.to_gray_image(image)

dft_res = cv2.dft(image)
res = cv2.idft(dft_res)
PIS(res)

6. cv2.inRange()

测试矩阵的元素是否在两个其他矩阵的值之间

  • 函数使用
1
cv2.inRange(src, upperb, lowerb)

当应用于矩阵时，src的每个元素都与upperb和lowerb中的对应元素进行校验。如果src中的元素在由upperb和lowerb给出的值之间，则dst的相应元素设置为255；否则设置为0。

  • 示例代码
1
2
3
4
5
6
7
8
9
10
11
12
mat = np.random.random([3,3,3,3])
res = cv2.inRange(mat, lowerb=0.1, upperb=0.5)

-->
res
array([[[[  0, 255,   0],
         [  0, 255,   0],
         [  0,   0,   0]],
		...
        [[  0, 255,   0],
         [  0,   0,   0],
         [255,   0,   0]]]], dtype=uint8)

7. cv2.invert()

求矩阵的逆

  • 函数使用
1
cv2.invert(src)

cv2.invert()求方阵src的逆，并将结果放在dst中。输入矩阵必须是浮点类型，结果矩阵与输入矩阵的类型相同。

  • 代码示例
1
2
3
4
5
6
7
8
mat_1 = np.random.random([3, 3])
res_1 = cv2.invert(mat_1)
print(np.matmul(mat_1, res_1[1]))

-->
[[ 1.00000000e+00  8.40366389e-18 -4.15195801e-17]
 [ 8.07609411e-17  1.00000000e+00 -2.12091444e-16]
 [ 1.37204127e-16  2.36371071e-17  1.00000000e+00]]

8. cv2.log()

计算矩阵逐元素的自然对数

1
2
3
4
5
6
7
8
mat = np.array([2.71828, 1, 2.7182 ** 2])
res = cv2.log(mat)

-->
res
array([[0.99999933],
       [0.        ],
       [1.99993979]])

9. cv2.LUT()

将矩阵转换为查找表的索引

  • 函数使用
1
cv2. LUT(src, lut)
  • 参数说明：
    • src：输入数据array，类型为8位整型（np.uin8)
    • lut：查找表，如果输入src是多通道的，例如是BGR三通到的图像，而查表是单通道的，则此时B、G、R三个通道使用的是同一个查找表
  • LUT函数对src中的每个元素的处理如下：

$$
\operatorname{dst}(I) \leftarrow \operatorname{lut}(\operatorname{src}(I)+\mathrm{d})
$$

  • 其中 d 取值为：
$$ d=\left\{\begin{array}{ll}0 & \text { if src has depth CV_8U } \\ 128 & \text { if src has depth CV_8S }\end{array}\right. $$

CV_8U：8位无符号整数，取值范围$(0,255)$

CV_8S：8位有符号整数，取值范围$(-128,127)$

  • 示例代码
1
2
3
4
5
image = mt.cv_rgb_imread('img1.jpg')
image = mt.image_resize(image, factor=0.3)
table = np.array([i * 1.5 for i in range (0,256)]).clip(0,255).astype('uint8')
res = cv2.LUT(image, table)
PIS(image, res)

10. cv2.magnitude()

计算二维向量的幅度

  • 函数使用
1
dst = cv2.magnitude(x, y)

其中参数 x,y 需要维度相同的矩阵，输出同维度欧式距离结果

$$ d s t_{i}=\sqrt{x_{i}^{2}+y_{i}^{2}} $$
  • 示例代码
1
2
3
4
5
6
7
8
9
10
mat_1 = np.ones([3,3])
mat_2 = np.ones([3,3])

res = cv2.magnitude(mat_1, mat_2)

-->
res
array([[1.41421356, 1.41421356, 1.41421356],
       [1.41421356, 1.41421356, 1.41421356],
       [1.41421356, 1.41421356, 1.41421356]])

11. cv2.Mahalanobis()

计算两个向量之间的马氏距离

$$
r_{\text {mahalonobis }}=\sqrt{(\vec{x}-\vec{\mu})^{T} \Sigma^{-1}(\vec{x}-\vec{\mu})}
$$

  • 马氏距离被定义为一点和高斯分布中心之间的向量距离；该距离使用该分布的逆协方差作为度量来计算。直观上，这类似于基础统计学中的标准分数(z-score),某一点到分布中心的距离是以该分布的方差为单位来衡量的。马氏距离则是该思路在高维空间中的推广。
  • 函数使用
1
cv2.Mahalanobis(vec1, vec2, icovar)
  • 参数说明：
    • vec1 对应需要测量的点 $X$
    • vec2 对应分布的均值
    • icovar 为协方差矩阵的逆
  • 示例代码：
1
2
3
4
vector1 =  np.ones([20])
vector2 =  np.ones([20])
icovar = np.ones([20, 20])
cv2.Mahalanobis(vector1, vector2, icovar)

12. cv2.max()

计算两个矩阵逐元素的最大值

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
vector1 = np.random.random([3, 3])
vector2 = np.random.random([3, 3])
max_vec = cv2.max(vector1, vector2)

-->
vector1
array([[0.97814374, 0.26007692, 0.99245652],
       [0.46002651, 0.0810055 , 0.04428289],
       [0.32043073, 0.729823  , 0.77140915]])
vector2
array([[0.18393401, 0.12411287, 0.66366459],
       [0.09300281, 0.60390766, 0.6715789 ],
       [0.07841699, 0.82945612, 0.52906616]])
max_vec
array([[0.97814374, 0.26007692, 0.99245652],
       [0.46002651, 0.60390766, 0.6715789 ],
       [0.32043073, 0.82945612, 0.77140915]])

13. cv2.mean()

计算矩阵元素的平均值

1
2
3
4
5
6
7
8
9
vector1 =  np.random.random([3, 3, 3, 3])
res = cv2.mean(vector1)


-->
res
(0.5031801734751784, 0.0, 0.0, 0.0)
vector1.mean()
0.5031801734751785

输出奇奇怪怪的四个值，还是直接用 numpy 的吧

14. cv2.meanStdDev()

计算矩阵元素的均值和标准差，输出的两个值分别为 均值 和 标准差

1
2
3
4
5
6
7
8
9
10
vector1 =  np.random.random([3, 3, 3, 3])
cv2.meanStdDev(vector1)

-->
res
(array([[0.50318017]]), array([[0.29869019]]))
vector1.std()
0.29869018720033463
vector1.mean()
0.5031801734751785

15. cv2.merge()

将多个单通道矩阵合并成一个多通道矩阵

  • 注意：根据需要合并的维度是否等于三会有不同的行为

维度不为 3 时会新增维度进行合并

1
2
3
4
5
6
7
8
vector1 = np.zeros([3,4])
vector2 = np.zeros([3,4])
vector3 = np.zeros([3,4])
res = cv2.merge([vector1, vector2, vector3])

-->
res.shape
(3,4,3)

维度等于三时会在第三个维度合并

1
2
3
4
5
6
7
8
vector1 = np.zeros([3,4,2])
vector2 = np.zeros([3,4,2])
vector3 = np.zeros([3,4,2])
res = cv2.merge([vector1, vector2, vector3])

-->
res.shape
(3, 4, 6)

16. cv2.min()

计算两个矩阵逐元素的最小值

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
vector1 = np.random.random([3, 3])
vector2 = np.random.random([3, 3])
min_vec = cv2.min(vector1, vector2)

-->
vector1
array([[0.93792068, 0.72915433, 0.27821069],
       [0.35437735, 0.42366726, 0.87919133],
       [0.51643521, 0.33966623, 0.18701177]])
vector2
array([[0.04305875, 0.80503805, 0.86890126],
       [0.85313452, 0.51452862, 0.25454594],
       [0.36831011, 0.62949488, 0.40295295]])
min_vec
array([[0.04305875, 0.72915433, 0.27821069],
       [0.35437735, 0.42366726, 0.25454594],
       [0.36831011, 0.33966623, 0.18701177]])

17. cv2.minMaxLoc()

在矩阵中寻找最小值和最大值

会输出处最大、最小值并返回下标

仅能处理二维数据

1
2
3
4
5
6
7
vector1 = np.random.random([9, 9])
res = cv2.minMaxLoc(vector1)


-->
res
(0.00038213610645077, 0.9792769368018108, (7, 0), (5, 4))

18. cv2.mixChannels()

打乱从输入矩阵到输出矩阵的通道

  • 函数使用
1
cv2.mixChannels([srcv], [dstv], fromTo)

从输入的一个或多个图像中重新排列通道并在输出的一个或多个图像中将它们分到特定的通道。

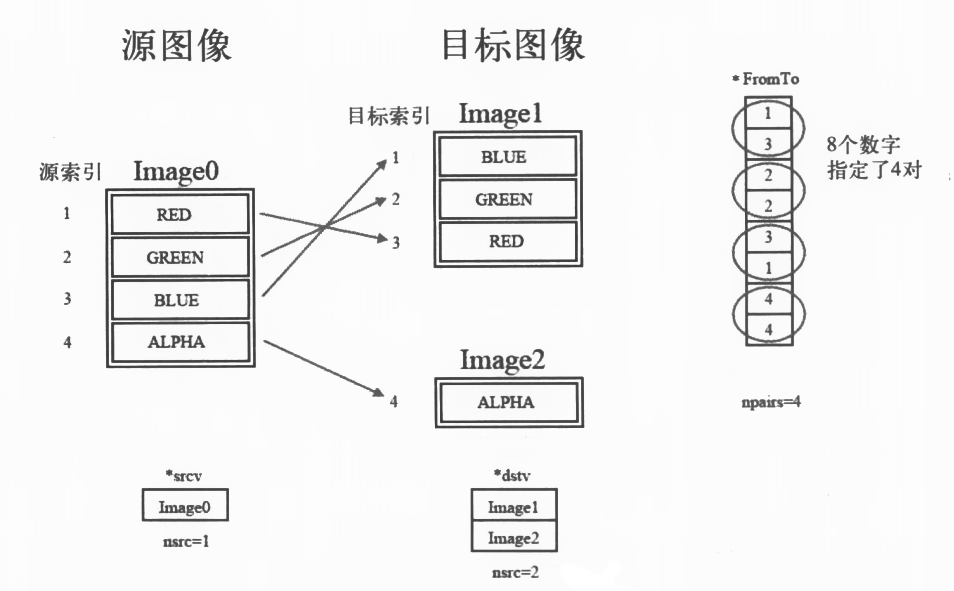
  • 参数说明
    • srcv 为数据源
    • dstv 为接收数据的载体
    • fromTo 为把 srcv 通道映射到 dstv 的映射关系
  • 示例代码
1
2
3
4
image_1 = mt.cv_rgb_imread('img1.jpg')
image_2 = np.zeros_like(image_1)
res = cv2.mixChannels([image_1], [image_2], [0,2,1,1,2,0])
PIS(image_1, res[0])

19. cv2.multiply()

计算两个矩阵的逐元素乘积

1
2
3
4
5
6
7
8
9
10
mat_1 = np.ones([3,3]) + 1
mat_2 = np.ones([3,3]) + 2

res = cv2.multiply(mat_1, mat_2)


-->
res
array([[6., 6., 6.],
       [6., 6., 6.],

20. cv2.mulTransposed()

计算矩阵和矩阵的转置的乘积

  • 函数使用
1
cv2.mulTransposed(src, aTa, scale=1, delta=None) -> dst

src 为矩阵，aTa 为计算标记

$$ d s t=\left\{\begin{array}{ll}\text { scale }^{*}(\text { src }-\text { delta })^{T}(\text { src }-\text { delta }) & \text { aTa }=\text { true } \\ \text { scale }^{*}(\operatorname{src}-\text { delta })(\operatorname{src}-\text { delta })^{T} & \text { aTa }=\text { false }\end{array}\right. $$
  • 示例代码
1
2
3
4
5
6
7
8
mat_1 = np.reshape(np.arange(9), [3,3]).astype('float32')
res = cv2.mulTransposed(mat_1, aTa=True)

np_res = np.matmul(mat_1.T, mat_1)

-->
(res == np_res).all()
True
1
2
3
4
5
6
7
8
9
mat_1 = np.reshape(np.arange(9), [3,3]).astype('float32')
delta = np.ones_like(mat_1)
res = cv2.mulTransposed(mat_1, aTa=True, scale=3, delta=delta)
    
-->
res
array([[ 90., 108., 126.],
       [108., 135., 162.],
       [126., 162., 198.]], dtype=float32)

21. cv2.norm()

计算矩阵/矩阵差的范数

函数cv2.norm()用于计算一个矩阵的范数，或者如果提供两个矩阵，该函数也可以计算两个矩阵间的各种距离范数。也可以计算cv2.SparseMat的范数，在这种情况下，范数的计算中忽略零项。

$$ \begin{array}{c} \|\operatorname{src} 1\|_{\infty, L 1, L 2} \\ \|\operatorname{src} 1-\operatorname{src} 2\|_{\infty, L 1, L 2} \end{array} $$
单个矩阵
  • 函数使用
1
cv2.norm(src1, normType=cv2.NORM_L2, mask=None)

  • mask 为和 src1 相同尺寸的矩阵，非零部分对应的 src1 会参与计算

  • normType

    • cv2.NORM_INF: $\|s r c 1\|_{\infty}=\max _{i} a b s\left(\operatorname{src1}_{i}\right) $
    • cv2.NORM_L1: $ \|s r c 1\|_{L 1}=\sum_{i} \operatorname{abs}\left(s r c 1_{i}\right) $
    • cv2.NORM_L2: $ \|\operatorname{src} 1\|_{12}=\sqrt{\sum \operatorname{src1}_{i}^{2} }$

  • 示例代码

1
2
3
4
5
6
mat_1 = np.reshape(np.arange(9), [3,3]).astype('float32')
res = cv2.norm(mat_1, normType=cv2.NORM_L2)
    
-->
res
14.2828568570857
两个矩阵
  • 函数使用
1
cv2.norm(src1, src2, normType=cv2.NORM_L2, mask=None)

  • mask 为和 src1 ，src2相同尺寸的矩阵，非零部分对应的 src1 ，src2会参与计算

  • normType

    • cv2.NORM_INF: $\|s r c 1 - s r c 2\|_{\infty}=\max _{i} a b s\left(\operatorname{src1}_{i} - s r c 2_i\right) $
    • cv2.NORM_L1: $ \|s r c 1- s r c 2\|_{L 1}=\sum_{i} \operatorname{abs}\left(s r c 1_{i}- s r c 2_i\right) $
    • cv2.NORM_L2: $ \|\operatorname{src1} - s r c 2\|_{12}=\sqrt{\sum (\operatorname{src1}_{i}-s r c 2_i)^{2} }$
    • cv2.NORM_RELATIVE_INF: $ \frac{\|\operatorname{src} 1-\operatorname{src} 2\|_{\infty}}{\|\operatorname{src} 2\|_{\infty}} $
    • cv2.NORM_RELATIVE_L1: $ \frac{\|s r c 1-s r c 2\|_{L 1}}{\|s r c 2\|_{L 1}} $
    • cv2.NORM_RELATIVE_L2: $ \frac{\|s r c 1-s r c 2\|_{L 2}}{\|s r c 2\|_{L 2}} $

  • 在所有情况下，src1和src2必须具有相同的尺寸和通道数。当通道数大于1时，将会对所有通道一起计算范数。

  • 示例代码：

1
2
3
4
5
6
7
mat_1 = np.reshape(np.arange(9), [3,3]).astype('float32')
mat_2 = np.ones([3,3]).astype('float32')
res = cv2.norm(mat_1, mat_2, normType=cv2.NORM_L1)
    
—->
res
29.0

22. cv2.normalize()

将矩阵中的元素标准化到某一数值内

  • 函数使用
1
cv2.normalize(src, dst, normType=cv2.NORM_L2, alpha=1, beta=0, mask=None)

  • normType：

    • cv2.NORM_INF: $ \|d s t\|_\infty=\max _{i} a b s\left(d s t_{i}\right)=\alpha $
    • cv2.NORM_L1: $ \|d s t\|_{L_1}=\sum_{i} \operatorname{abs}\left(d s t_{i}\right)=\alpha $
    • cv2.NORM_L2: $ \|d s t\|_{L2}=\sqrt{\sum_{i} d s t_{i}^{2}}=\alpha $
    • cv2.NORM_MINMAX: 映射到区间$ [ \alpha, \beta]$

  • 示例代码

1
2
3
4
5
6
7
8
9
10
11
vector1 = np.random.random([3, 3])
vector2 = np.zeros_like(vector1)

res = cv2.normalize(vector1, vector2, norm_type = cv2.NORM_MINMAX, alpha=5, beta=2)


-->
res
array([[3.94229448, 2.        , 5.        ],
       [3.97560615, 4.81894702, 2.56644533],
       [2.1542595 , 4.22382767, 4.71024315]])

23. cv2.perspectiveTransform()

实现一系列向量的透视矩阵变换

  • 函数使用
1
cv2.perspectiveTransform(src, mtx)

cv2.perspectiveTransform() 函数执行一系列点（而不是像素）的平面投影变换。输入矩阵应为二通道或三通道矩阵，在这两种情况下，矩阵mtx尺寸分别为 $3×3$ 与 $4×4$ .cv2.perspectiveTransform()首先将src的每个元素转换为长度为src, channels +1的向量，其中附加维度（投影维度）初始化为1.0。这也称为齐次坐标。然后将每个扩展向量乘以mtx,并将结果重新排列为（新）投影坐标的值（然后将附加维度抛弃，因为在此操作以后始终为1.0)。

  • 注意：请再注意一点，此例程用于转换一系列点，而不是图像。如果要将透视变换应用于图像，你实际上不是转换单个像素，而是将它们从图像中的一个位置移动到另一个位置。这是cv2.warpPerspective()的工作。
$$ \left[\begin{array}{l}x^{\prime} \\ y^{\prime} \\ z^{\prime} \\ w^{\prime}\end{array}\right] \rightarrow[m t x]\left[\begin{array}{l}x \\ y \\ z \\ 1\end{array}\right] $$
  • 示例代码
1
2
3
4
5
6
7
8
9
10
11
points = np.ones([5, 2])
matrix = np.eye(2)
res = cv2.perspectiveTransform(points, matrix) 

-->
res
array([[1., 1.],
       [1., 1.],
       [1., 1.],
       [1., 1.],
       [1., 1.]])

示例源码

参考资料

  • 《学习 OpenCV3》 第五章


文章链接：
https://www.zywvvd.com/notes/study/image-processing/opencv/opencv-matrix-op/opencv-matrix-op-part2/

“觉得不错的话，给点打赏吧 ୧(๑•̀⌄•́๑)૭”

微信二维码

微信支付

支付宝二维码

支付宝支付

Image_Processing > OpenCV
#OpenCV #Image_Processing
OpenCV - 矩阵操作 Part 2
https://www.zywvvd.com/notes/study/image-processing/opencv/opencv-matrix-op/opencv-matrix-op-part2/
作者
Yiwei Zhang
发布于
2022年3月2日
许可协议