OpenCV 直方图

本文最后更新于：2024年5月7日下午

在分析图像、物体和视频信息的时候，我们经常用直方图来表达我们关注的信息。直方图可以用来表达很多不同的信息，例如物体的颜色分布，物体的边缘梯度模板或是以概率分布的形式表达当前对物体位置的估计。本文记录 OpenCV 中的直方图相关操作。

直方图概述

直方图在计算机视觉中应用广泛。例如，通过判断帧与帧之间边缘和颜色的统计量是否出现巨大变化，来检测视频中场景的变换。通过使用兴趣点邻域内的特征组成的直方图，来辨识兴趣点。若将边缘、颜色、角点等等的直方图作为特征，可以使用分类器来进行目标识别。提取视频中的颜色或边缘直方图序列，可以用来判断视频是否拷贝自网络。这样的应用数不胜数，直方图可以说是计算机视觉领域中的经典工具之一。

直方图只是简单地将数据归入预定义的组，并在每个组内进行计数。也可以选择对数据提取特征，再对特征进行计数，这里的特征可以是梯度的长度、梯度的方向、颜色或者其他任何可以反映数据特点的特征。
原始数据可以是任意东西，因此直方图可以作为一种方便的工具来表达图片中的信息。

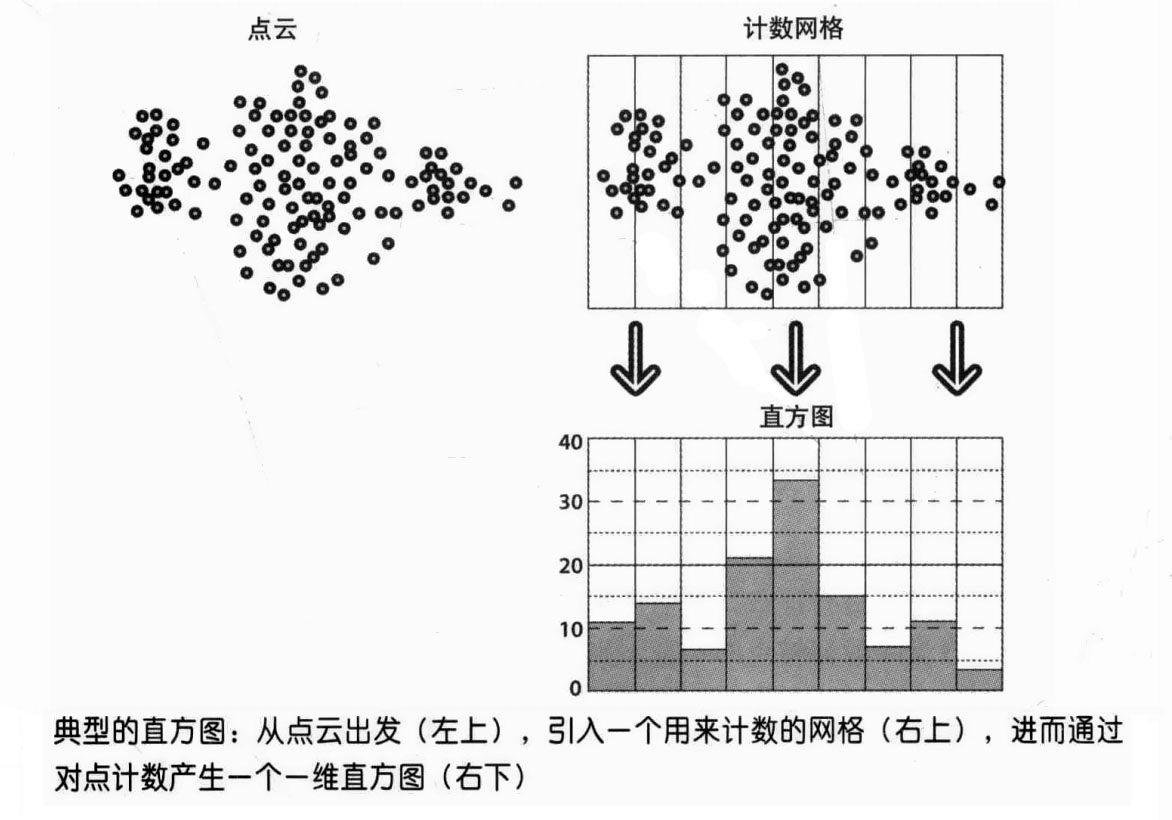
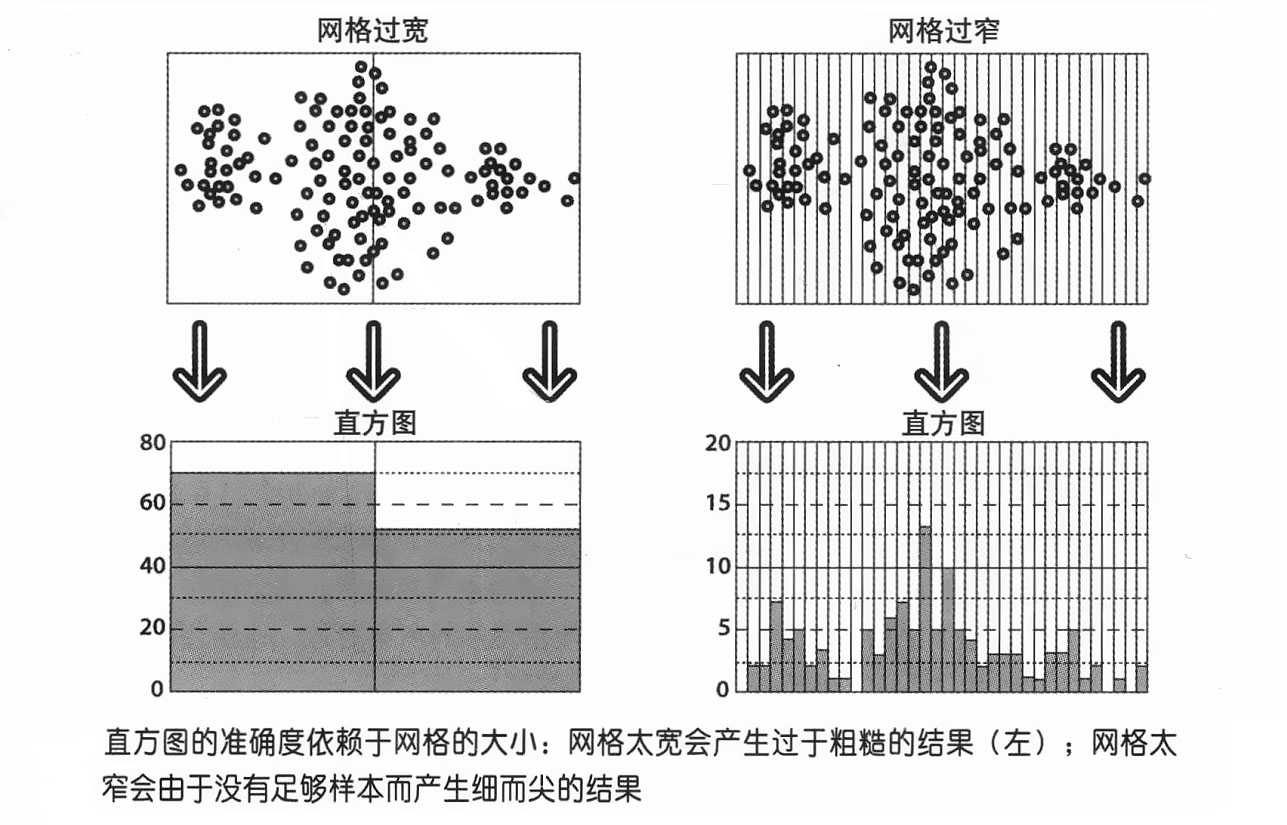
如果原始数据是连续分布的，可以通过离散量化的方式来生成直方图注1，但这种方法会引发一些问题。如果用来量化的网格选得过宽，量化的结果会过于粗糙，我们会丢失一些数据分布的结构信息。如果网格过窄，每组中没有足够的数据点来准确估计数据分布，直方图里就会出现一些小的、细且尖的矩形。

OpenCV提供一种数据类型来表达直方图，这个数据类型可以表达一维至多维的直方图，并包括必要的数据以支持均匀或非均匀的组宽。
尽管用来表示直方图的数据结构和用来表示矩阵或是图像的数据结构相同，由于对这种数据结构的解释有所不同，所以直方图配有一系列用来完成特定任务的新操作。本节介绍一些与直方图相关的简单操作，并且讲解如何用先前讲述的矩阵操作来完成一些重要的直方图操作。

直方图统计

cv2.calcHist

参考链接

直方图归一化

当构造直方图时，我们首先需要将信息放入在各个区间。然而，一旦完成这些，我们有时还会希望将直方图变为归一化的形式，这时每个区间恰好表示的是该区间内的信息占总体的百分比。

cv2.normalize

规范化数组的范围或值范围。

官方文档

函数使用

cv2.normalize(
	src, 				# 输入数组。
	dst[, 				# 与 src 大小相同的输出数组。
	alpha[, 			# 归一范数目标值 / 最大最小规范化中的下限
	beta[,				# 范数归一化时该值无效 / 最大最小规范化中的上限
    norm_type[, 		# 归一化方法
    dtype[, 			# 当为负数时，输出数组的类型与 src 相同；否则，它具有与 src 相同的通道数和深度
    mask]]]]]			# 数据蒙版（可选）
    ) ->	
    dst

函数标准化缩放和移动输入数组元素，以便：

$$ \| dst \|_{L_{p}}= alpha $$

其中 P 值与 norm_type 对应关系为:

norm_type	P 值
cv2.NORM_INF	inf
cv2.NORM_L1	1
cv2.NORM_L2	2

或者当 norm_type 为 cv2.NORM_MINMAX 时：

$$
\min _{I} \operatorname{dst}(I)= alpha, \max _{I} \operatorname{dst}(I)= bet
$$

可选 mask 参数指定要规范化的子数组。这意味着在子数组上计算范数或 min-n-max，然后修改该子数组以进行归一化。
示例代码

img = mt.cv_rgb_imread('img.jpg', gray=True)
hist = cv2.calcHist([img], [0], None, [256], [0, 255]) 
res = cv2.normalize(hist, None, alpha=1, norm_type=cv2.NORM_L2)
PIS(hist[:, 0], res[:, 0])


-->
np.sum(res**2)
1.0

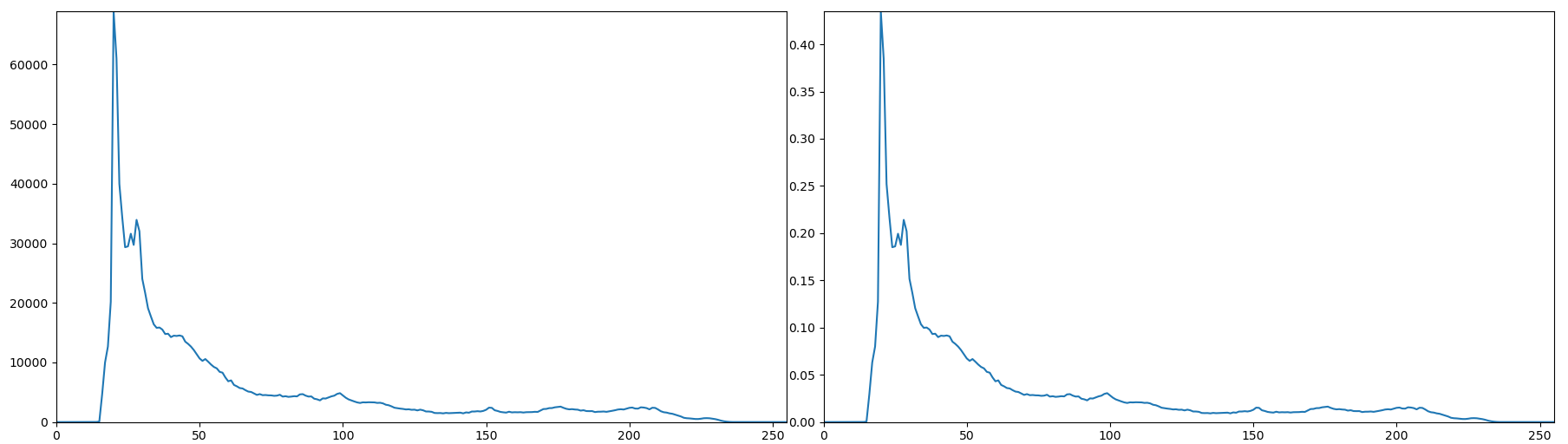
直方图二值化

cv2.threshold

可以运用 cv2.threshold 函数将直方图进行二值化操作
示例代码

img = mt.cv_rgb_imread('img.jpg', gray=True)
hist = cv2.calcHist([img], [0], None, [256], [0, 255])
res = cv2.normalize(hist, None, alpha=0, beta=255, norm_type=cv2.NORM_MINMAX)
thre, res_hist = cv2.threshold(res, 50, 0, cv2.THRESH_TOZERO)
PIS(hist[:, 0], res_hist[:, 0])

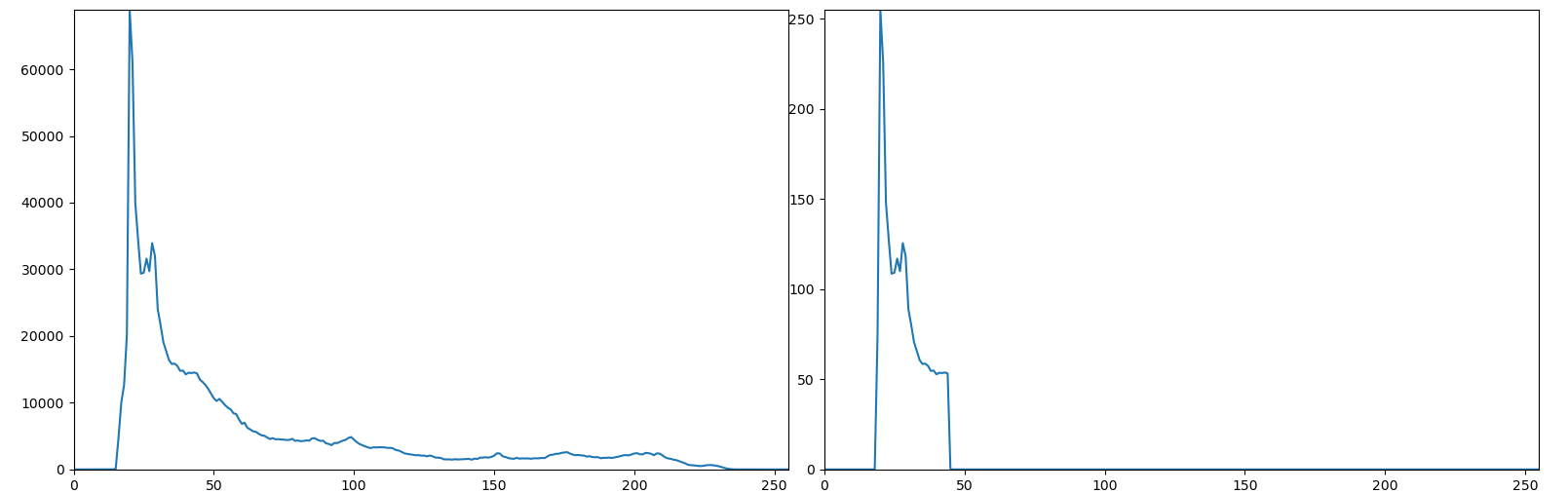
找出最显著的区间

有时你希望能找出所有元素个数高于某个给定阈值的区间，有时你只是希望能找出有最多元素的区间。这种情况多发生在使用直方图来表示概率分布的时候。这时你可以选择使用cv2.minMaxLoc()。

cv2.minMaxLoc

查找数组中的全局最小值和最大值。

官方文档

函数使用

cv2.minMaxLoc(
	src[, 				# 单通道二维数组
	mask]				# 可选参数，用于筛选一个子数组
	) ->	
	minVal, 			# 最小值
	maxVal, 			# 最大值
	minLoc, 			# 最小值下标
	maxLoc				# 最大值下标

示例代码

img = mt.cv_rgb_imread('img.jpg', gray=True)
hist = cv2.calcHist([img], [0], None, [256], [0, 255])
min_val, max_val, min_loc, max_loc = cv2.minMaxLoc(hist)


-->
min_val, max_val, min_loc, max_loc
(0.0, 68891.0, (0, 0), (0, 20))

直方图比较

不同直方图可以做距离度量，得到直方图之间的相似性。

cv2.compareHist

官方文档

函数使用

cv2.compareHist(	
	H1, 			# 直方图1
	H2, 			# 直方图2，尺寸和 H1 相同
	method			# 比较方法
	) ->	
	retval			# 距离

method: HistCompMethods

可选值	含义	计算方法
cv2.HISTCMP_CORREL	相关性	$d\left(H_{1}, H_{2}\right)=\frac{\sum_{I}\left(H_{1}(I)-\bar{H}_{1}\right)\left(H_{2}(I)-\bar{H}_{2}\right)}{\sqrt{\sum_{I}\left(H_{1}(I)-\bar{H}_{1}\right)^{2} \sum_{I}\left(H_{2}(I)-\bar{H}_{2}\right)^{2}}}$,其中 $\bar{H}_{k}=\frac{1}{N} \sum_{J} H_{k}(J)$
cv2.HISTCMP_CHISQR	卡方	$ d\left(H_{1}, H_{2}\right)=\sum_{I} \frac{\left(H_{1}(I)-H_{2}(I)\right)^{2}}{H_{1}(I)} $
cv2.HISTCMP_INTERSECT	交集法	$d\left(H_{1}, H_{2}\right)=\sum_{I} \min \left(H_{1}(I), H_{2}(I)\right) $
cv2.HISTCMP_BHATTACHARYYA	巴特查里亚距离	$ d\left(H_{1}, H_{2}\right)=\sqrt{1-\frac{1}{\sqrt{\bar{H}_{1} \bar{H}_{2} N^{2}}} \sum_{I} \sqrt{H_{1}(I) \cdot H_{2}(I)}} $
cv2.HISTCMP_HELLINGER	巴特查里亚距离	cv2.HISTCMP_BHATTACHARYYA 的别名
cv2.HISTCMP_CHISQR_ALT	另一种卡方	$ d\left(H_{1}, H_{2}\right)=2 * \sum_{I} \frac{\left(H_{1}(I)-H_{2}(I)\right)^{2}}{H_{1}(I)+H_{2}(I)} $
cv2.HISTCMP_KL_DIV	KL散度	$ d\left(H_{1}, H_{2}\right)=\sum_{I} H_{1}(I) \log \left(\frac{H_{1}(I)}{H_{2}(I)}\right) $

示例代码

1
2
3

hist1 = np.random.random([80]).astype('float32')
hist2 = np.random.random([80]).astype('float32')
dis = cv2.compareHist(hist1, hist2, method=cv2.HISTCMP_KL_DIV)

EMD (Earth mover’s distance) 距离

光照的变化会使颜色值产生大量的偏移，虽然这种偏移倾向于并不改变颜色直方图的形状，但目前我们见到的距离度量方法都对直方图颜色位置的移动束手无策。核心的困难是对于两个形状相同、但只是相对平移的两个直方图，距离度量会给出一个很大的值。我们希望能找到一个对这种平移不敏感的距离度量方法。

EMD 就是这样一种距离度量。它的基本思路是，通过将一部分（或全部）直方图搬到一个新位置，度量花多大的功夫才能把一个直方图“搬到”另一个直方图里。EMD距离可以在任意维度下工作。

cv2.EMD

计算两个加权点配置之间的“最小工作/推土机”距离。

官方文档

函数使用

cv2.EMD(
	signature1,
	signature2,
	distType,
	[cost,
	[lowerBound,
	[flow]]]
) - >
retval, lowerBound, flow

参数说明：
- signature1
  
  第一个签名，一个$ size1×dims+1 $浮点矩阵。
  
  每行存储点权重，后跟点坐标。如果使用用户定义的成本矩阵，则允许该矩阵具有单列（仅权重）。权重必须是非负的并且至少有一个非零值。
- signature2
  
  与 signature1 格式相同的第二个签名，尽管行数可能不同。
  
  总重量可能不同。在这种情况下，一个额外的“虚拟”点被添加到签名 1 或签名 2。权重必须是非负的并且至少有一个非零值。
- distType
  
  距离类型
- cost
  
  用户定义的 $size1×size2 $ 成本矩阵。此外，如果使用成本矩阵，则无法计算下边界 lowerBound 因为它需要一个度量函数。
- lowerBound
  
  可选输入/输出参数：两个签名之间距离的下边界，即质心之间的距离。如果使用用户定义的成本矩阵，点配置的总权重不相等，或者签名仅由权重组成（签名矩阵只有一列），则可能无法计算下边界。您必须初始化 lowerBound 。如果计算的质心之间的距离大于或等于 lowerBound（这意味着签名足够远），则该函数不计算 EMD。在任何情况下，lowerBound 都设置为返回时计算的质心之间的距离。因此，如果要计算质心和 EMD 之间的距离，lowerBound 应设置为 0。
- flow
  
  结果 $size1×size2$ 流矩阵： $flow_{i,j} $是从 signature1 的第 $i $个点到 signature2 的第 $j $个点的流。
示例代码 (私有 cost 定义)

hist1 = np.array([0,0,1,2,3,4,5,6,0,0], dtype='float32')
hist2 = np.array([1,2,3,4,5,6,0,0,0,0], dtype='float32')

cost = np.ones([len(hist1), len(hist1)], dtype='float32')

retval, lowerBound, flow = cv2.EMD(hist1, hist2, cv2.DIST_USER, cost)


-->
retval
1.0
flow
array([[0., 0., 0., 0., 0., 0., 0., 0., 0., 0.],
       [0., 0., 0., 0., 0., 0., 0., 0., 0., 0.],
       [1., 0., 0., 0., 0., 0., 0., 0., 0., 0.],
       [0., 2., 0., 0., 0., 0., 0., 0., 0., 0.],
       [0., 0., 3., 0., 0., 0., 0., 0., 0., 0.],
       [0., 0., 0., 4., 0., 0., 0., 0., 0., 0.],
       [0., 0., 0., 0., 5., 0., 0., 0., 0., 0.],
       [0., 0., 0., 0., 0., 6., 0., 0., 0., 0.],
       [0., 0., 0., 0., 0., 0., 0., 0., 0., 0.],
       [0., 0., 0., 0., 0., 0., 0., 0., 0., 0.]], dtype=float32)

示例代码 (官方距离定义)

hist1 = np.array([0,0,1,2,3,4,5,6,0,0], dtype='float32')
hist2 = np.array([1,2,3,4,5,6,0,0,0,0], dtype='float32')

signature_1 = np.concatenate([[hist1], [np.arange(len(hist1))]]).astype('float32').T
signature_2 = np.concatenate([[hist2], [np.arange(len(hist2))]]).astype('float32').T

retval, lowerBound, flow = cv2.EMD(signature_1, signature_2, cv2.DIST_L1)


-->
flow
array([[0., 0., 0., 0., 0., 0., 0., 0., 0., 0.],
       [0., 0., 0., 0., 0., 0., 0., 0., 0., 0.],
       [1., 0., 0., 0., 0., 0., 0., 0., 0., 0.],
       [0., 2., 0., 0., 0., 0., 0., 0., 0., 0.],
       [0., 0., 3., 0., 0., 0., 0., 0., 0., 0.],
       [0., 0., 0., 0., 0., 4., 0., 0., 0., 0.],
       [0., 0., 0., 3., 0., 2., 0., 0., 0., 0.],
       [0., 0., 0., 1., 5., 0., 0., 0., 0., 0.],
       [0., 0., 0., 0., 0., 0., 0., 0., 0., 0.],
       [0., 0., 0., 0., 0., 0., 0., 0., 0., 0.]], dtype=float32)

反向投影

反向投影(Back Projection)是计算像素和直方图模型中像素吻合度的一种方法。

反向投影是一种记录给定图像中的像素点如何适应直方图模型像素分布的方式，简单来讲，反向投影就是首先计算某一特征的直方图模型，然后使用模型去寻找图像中存在的特征。反向投影在某一位置的值就是原图对应位置像素值在原图像中的总数目。

cv2.calcBackProject

计算直方图的反投影

官方文档

和cv2.clacHist()类似，反向投影从输入图像的指定通道中计算出一个向量，但不同于前者在向直方图中记录累计值，反向投影从输入的直方图中读取当前像素对应的计数值作为结果。从统计学的视角来看，如果将输入的直方图视为某个物体上特定的向量（颜色）的一个（先验）概率分布，那么反向投影就是计算图片上某个特定部分来自该先验分布（即属于物体的一部分）的概率。
这是 CamShift 颜色对象跟踪器的近似算法。
函数使用

cv2.calcBackProject(
	images, 			# 源数据数组。
						  它们都应该具有相同的深度、CV_8U、CV_16U 或 CV_32F，以及相同的大小。它们中的每一个都可以有任意数量的通道。
	channels, 			# 用于计算反投影的通道列表。
						  通道的数量必须与直方图的维度相匹配。
						  第一个数组通道从 0 到 images[0].channels()-1 进行计数，
						  第二个数组通道从 images[0].channels() 到 images[0].channels() + images[1].channels()，依此类推。
	hist, 				# 直方图。
	ranges, 			# 每个维度中直方图 bin 边界的数组数组。
	scale[, 			# 输出反投影的可选比例因子。
	dst]
	) ->	
	dst

示例图像


sample.jpeg	target.jpeg

示例代码

# 读取图片
sample = cv2.imread("sample.jpeg")
target = cv2.imread("target.jpeg")
# 转换为HSV格式
roi_hsv = cv2.cvtColor(sample, cv2.COLOR_BGR2HSV)
target_hsv = cv2.cvtColor(target, cv2.COLOR_BGR2HSV)

# 计算图像直方图
roiHist = cv2.calcHist([roi_hsv], [0, 1], None, [64, 64], [0, 180, 0, 256])
# 图像归一化处理
cv2.normalize(roiHist, roiHist, 0, 255, cv2.NORM_MINMAX)
# 获取直方图的反向投影
dst = cv2.calcBackProject([target_hsv], [0, 1], roiHist, [0, 180, 0, 256], 1)

PIS(dst, cmap='gray')