OpenCV 单应性矩阵计算函数 findHomography

本文最后更新于：2024年8月30日晚上

在计算机视觉领域，单应性是一个非常重要的概念，本文记录单应性矩阵的概念以及 OpenCV 计算函数。

概念介绍

齐次坐标（Homogeneous Coordinate）

一幅2D图像上的非齐次坐标为 $(x,y)$，而齐次坐标为 $(x,y,1)$，也可以写成 $(x/z,y/z,1)$或 $(x,y,z)$。齐次坐标有很多好处，比如可以很清楚的确定一个点在不在直线上：

$T(x)*I=0$, $T$ 表示转置矩阵；

还可以描述无穷远点：(x,y,0)；

还可以把平移和旋转写到一个矩阵里（也有不愿意这么干的，摄影测量里用的都是非齐次坐标，平移和旋转分开写）；

单应性矩阵（Homography Matrix）

两个不同视角图像上的点对，其在齐次坐标 homogeneous coordinate下可以用一个射影变换 projective transformation 表述，即 $x_1 = H*x_2$。

二维和三维的图示如下：

射影变换也叫“单应”–Homography，“Homo”前缀就是same的意思，表示“同”，homography就是用同一个源产生的graphy，中文译过来大概就是“单应”。

上面式子中的矩阵 $H$ 就叫单应性矩阵。上式中的 $x_1$ 和 $x_2$都是$3\times1$的齐次坐标，因此 $H$ 是一个 $3\times3$的矩阵：

$$ s \begin{bmatrix} x^{'} \\ y^{'} \\ 1 \end{bmatrix} = \mathbf{H} \begin{bmatrix} x \\ y \\ 1 \end{bmatrix} = \begin{bmatrix} h_{11} & h_{12} & h_{13} \\ h_{21} & h_{22} & h_{23} \\ h_{31} & h_{32} & h_{33} \end{bmatrix} \begin{bmatrix} x \\ y \\ 1 \end{bmatrix} $$

自由度 DoF (degrees of freedom)

如果给定一个单应 $H={h_{ij}}$，给它的元素乘上同一个数 $a$，得到的的单应 $aH$和 $H$ 作用相同，因为新单应无非把齐次点 $x_1$ 变成了齐次点 $ax_1$，都是一回事。因此我们可以把 $a$ 换成 $1/h_{33}$，那么 $H$ 就变成了只有8个自由元素的矩阵。

那么需要多少个点对求解这个 $H$ 呢？如果需要唯一解的话，需要4个点对（对应8个方程，去解 $H$ 中的8个未知数）。

常用的归一化方法有：

$ h_{33} = 1 $
$ h_{11}^2 + h_{12}^2 + h_{13}^2 + h_{21}^2 + h_{22}^2 + h_{23}^2 + h_{31}^2 + h_{32}^2 + h_{33}^2 = 1 $

适用场景

平面和图像平面

由两个摄像机位置观察到的平面

绕其投影轴旋转的相机，相当于认为这些点位于无穷远处的平面上

单应性矩阵求解

首先，我们假设两张图像中的对应点对齐次坐标为(x’,y’,1)和(x,y,1)，单应矩阵H定义为：

$$ \boldsymbol{H}=\begin{bmatrix}h_{11}&h_{12}&h_{13}\\h_{21}&h_{22}&h_{23}\\h_{31}&h_{32}&h_{33}\end{bmatrix} $$ 则有： $$ s \begin{bmatrix} x^{'} \\ y^{'} \\ 1 \end{bmatrix} = \mathbf{H} \begin{bmatrix} x \\ y \\ 1 \end{bmatrix} = \begin{bmatrix} h_{11} & h_{12} & h_{13} \\ h_{21} & h_{22} & h_{23} \\ h_{31} & h_{32} & h_{33} \end{bmatrix} \begin{bmatrix} x \\ y \\ 1 \end{bmatrix} $$ 矩阵展开后有3个等式，将第3个等式代入前两个等式中可得： $$ x^{\prime}=\frac{h_{11}x+h_{12}y+h_{13}}{h_{31}x+h_{32}y+h_{33}}\\y^{\prime}=\frac{h_{21}x+h_{22}y+h_{23}}{h_{31}x+h_{32}y+h_{33}} $$

根据上文对单应性矩阵自由度的讨论结果，有两种归一化方法：

令 $s = h_{33} = 1$，那么上述等式变为：

$$ x^{\prime}=\frac{h_{11}x+h_{12}y+h_{13}}{h_{31}x+h_{32}y+1}\\y^{\prime}=\frac{h_{21}x+h_{22}y+h_{23}}{h_{31}x+h_{32}y+1} $$

将 $H$ 添加约束条件，将 $H$ 矩阵模与 $s$ 变为1，则等式如下：
$$ \begin{aligned}&x^{\prime}=\frac{h_{11}x+h_{12}y+h_{13}}{h_{31}x+h_{32}y+h_{33}}\\&y^{\prime}=\frac{h_{21}x+h_{22}y+h_{23}}{h_{31}x+h_{32}y+h_{33}}\\&h_{11}^{2}+h_{12}^{2}+h_{13}^{2}+h_{21}^{2}+h_{22}^{2}+h_{23}^{2}+h_{31}^{2}+h_{32}^{2}+h_{33}^{2}=1\end{aligned} $$

这里我们用模长为 1 的归一化方法继续推导：

$$ (h_{31}x+h_{32}y+h_{33})x^{\prime} = h_{11}x+h_{12}y+h_{13}\\(h_{31}x+h_{32}y+h_{33})y^{\prime} = h_{21}x+h_{22}y+h_{23} $$ 整理，得到： $$ h_{11}x+h_{12}y+h_{13}-h_{31}xx^{\prime}-h_{32}yx^{\prime}-h_{33}x^{\prime}=0\\h_{21}x+h_{22}y+h_{23}-h_{31}xy^{\prime}-h_{32}yy^{\prime}-h_{33}y^{\prime}=0 $$ 假如我们得到了两幅图片中对应的N个点对（特征点匹配对），那么可以得到如下线性方程组： $$ \left[\begin{array}{ccccccc}x_1&y_1&1&0&0&0&-x_1x_1'&-y_1x_1'&-x_1'\\0&0&0&x_1&y_1&1&-x_1y_1'&-y_1y_1'&-y_1'\\\\\\\\\\\\\\\\\end{array}\right]\left[\begin{array}{c}h_{11}\\h_{12}\\h_{13}\\h_{21}\\h_{22}\\h_{23}\\h_{31}\\h_{32}\\h_{33}\end{array}\right]=\left[\begin{array}{c}0\\0\\\\\\\\\\\\\\\\\end{array}\right] $$ 写成矩阵形式： $$ \begin{array}{cccc}2\mathrm{Nx9}&9\mathrm{x1}&&2\mathrm{Nx1}\\\mathbf{A}&\mathbf{h}&=&\mathbf{0}\end{array} $$

由于单应矩阵H包含了 $||H||=1$ 约束，因此根据上图的线性方程组，8自由度的H我们至少需要 4 对对应的点才能计算出单应矩阵。这也回答了前面图像校正中提到的为何至少需要4个点对的根本原因。

但是，以上只是理论推导，在真实的应用场景中，我们计算的点对中都会包含噪声。比如点的位置偏差几个像素，甚至出现特征点对误匹配的现象，如果只使用4个点对来计算单应矩阵，那会出现很大的误差。因此，为了使得计算更精确，一般都会使用远大于4个点对来计算单应矩阵。另外上述方程组采用直接线性解法通常很难得到最优解，所以实际使用中一般会用其他优化方法，如奇异值分解、Levenberg-Marquarat（LM）算法（后续文章会介绍）等进行求解。

如何根据标定图得到单应矩阵

经过前面一系列的介绍，我们应该大致明白如何根据打印的棋盘标定图和拍摄的照片来计算单应矩阵H。我们来总结一下大致过程。

打印一张棋盘格标定图纸，将其贴在平面物体的表面。
拍摄一组不同方向棋盘格的图片，可以通过移动相机来实现，也可以移动标定图片来实现。
对于每张拍摄的棋盘图片，检测图片中所有棋盘格的特征点（角点，也就是下图中黑白棋盘交叉点，中间品红色的圆圈内就是一个角点）。我们定义打印的棋盘图纸位于世界坐标系Zw=0的平面上，世界坐标系的原点位于棋盘图纸的固定一角（比如下图中黄色点）。像素坐标系原点位于图片左上角。

因为棋盘标定图纸中所有角点的空间坐标是已知的，这些角点对应在拍摄的标定图片中的角点的像素坐标也是已知的，如果我们得到这样的N>=4个匹配点对（越多计算结果越鲁棒），就可以根据LM等优化方法得到其单应矩阵H。

应用

图像拼接

通过图像特征点匹配+RANSAC可以获得图像之间的单应性矩阵，然后把其中一个图像通过这个矩阵投影到另一个图像上就完成了基本的拼接。

相机内参标定

对一个棋盘格拍照，棋盘格的世界坐标系是用户任意设定的，标定的时候，默认世界坐标系就是以标定板左上角点为原点，$z$ 轴垂直于标定板，$xoy$ 面与标定板重合的三维直角坐标系。

棋盘格的格子长度已知，因此可以知道各个角点的世界坐标系坐标 $XYZ（Z=0）$。由于 $Z=0$，因此可以忽略掉 $Z$ 这个维度，世界坐标系中某个坐标 $(X,Y,Z,1)$ 到图像坐标 $(x,y,1)$ 的变换就等价于 $(X,Y,1)$ 到图像坐标 $(x,y,1)$ 的变换。此时的变换矩阵就由 $3\times4$ 变为 $3\times3$，成为了单应性矩阵。

因此用 4 个角点就可以计算 $H$ 的8个参数。以不同的角度对棋盘格拍摄 3 张就可以得到 3 个 $H$，如果用张正友标定法，就可以得到6个约束方程，可以求解B矩阵（对称矩阵）的6个未知参数，进而通过Cholesky分解求解出内参矩阵A的参数。

像素坐标系和世界坐标系下的坐标映射关系：

$$ \begin{bmatrix}u\\\nu\\1\end{bmatrix}=s\begin{bmatrix}f_x&\gamma&u_0\\0&f_y&\nu_0\\0&0&1\end{bmatrix}\begin{bmatrix}r_1&r_2&t\end{bmatrix}\begin{bmatrix}x_W\\y_W\\z_W\end{bmatrix} $$ 相机下的单应性（Homography）变换，可以简单的理解为它用来描述物体在世界坐标系和像素坐标系之间的位置映射关系。对应的变换矩阵称为单应性矩阵。在上述式子中，单应性矩阵定义为： $$ H=s\begin{bmatrix}f_x&\gamma&u_0\\0&f_y&\nu_0\\0&0&1\end{bmatrix}\begin{bmatrix}r_1&r_2&t\end{bmatrix}=sM\begin{bmatrix}r_1&r_2&t\end{bmatrix} $$ 其中，M是内参矩阵。 $$ M=\begin{bmatrix}f_x&\gamma&u_0\\0&f_y&\nu_0\\0&0&1\end{bmatrix} $$

从单应矩阵定义式子来看，它同时包含了相机内参和外参。

图像校正

用单应矩阵进行图像矫正的例子如下图所示，最少需要四个对应点对就可以实现。

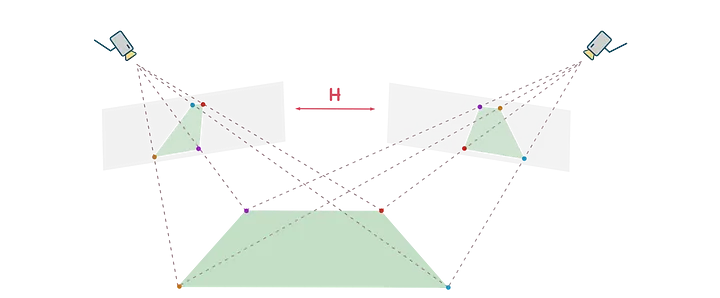
视角变换

单应矩阵用于视角变换的例子如下图所示，可以方便地将左边普通视图转换为右图的鸟瞰图。

增强现实（AR）

平面二维标记图案（marker）经常用来做AR展示。根据marker不同视角下的图像可以方便的得到虚拟物体的位置姿态并进行显示，如下图所示。

cv2.findHomography 函数

官方文档

1	`cv2.findHomography( srcPoints, dstPoints[, method[, ransacReprojThreshold[, mask[, maxIters[, confidence]]]]] ) -> retval, mask`

参数说明：

参数	含义	备注
srcPoints	源平面的坐标矩阵，可以是CV_32FC2类型，也可以是`vector<Point2f>`类型
dstPoints	目标平面的坐标矩阵，可以是CV_32FC2类型，也可以是`vector<Point2f>`类型
method	计算单应矩阵所使用的方法。	0 - 利用所有点的常规方法 RANSAC - RANSAC-基于RANSAC的鲁棒算法 LMEDS - 最小中值鲁棒算法 RHO - PROSAC-基于PROSAC的鲁棒算法
ransacReprojThreshold	将点对视为内点的最大允许重投影错误阈值（仅用于RANSAC和RHO方法）	如果重投影误差大于该阈值则被认为是外点（即错误匹配点对）。若srcPoints和dstPoints是以像素为单位的，则该参数通常设置在1到10的范围内。
mask	可选输出掩码矩阵，通常由鲁棒算法（RANSAC或LMEDS）设置。	请注意，输入掩码矩阵是不需要设置的。
maxIters	RANSAC算法的最大迭代次数。	默认为2000。
confidence	可信度	取值0-1

函数功能：该函数能够找到并返回源平面和目标平面之间的转换矩阵H，以便于反向投影错误率达到最小。

$$ s_i\begin{bmatrix}x_i'\\y_i'\\1\end{bmatrix}\sim H\begin{bmatrix}x_i\\y_i\\1\end{bmatrix} $$ 反投影误差计算方法： $$ \sum_i\left(x_i^{\prime}-\frac{h_{11}x_i+h_{12}y_i+h_{13}}{h_{31}x_i+h_{32}y_i+h_{33}}\right)^2+\left(y_i^{\prime}-\frac{h_{21}x_i+h_{22}y_i+h_{23}}{h_{31}x_i+h_{32}y_i+h_{33}}\right)^2 $$

如果方法参数method值为默认值0，则该函数使用所有点对来计算具有简单最小二乘的初始单应性估计。但并不是所有点对都合适刚性透视变换(即存在一些外点,匹配错误点对),那么这个初始估计就很差。在这种情况下，可以使用RANSAC、LMeDS和RHO等算法尝试对应点对的许多不同子集，使用该子集和简单最小二乘算法估计单应矩阵，然后计算单应性矩阵的质量(内点的数量或重投影误差)。最后使用最佳子集来差生单应性矩阵的初始估计。有了初始的单应性的估计矩阵后，都会采用Levenberg-Marquardt方法进行细化，以进一步减少重投影误差。

【注】：该函数返回归一化后的H矩阵，若无法估计H矩阵，则返回一个空矩阵Mat。

Python 实现

图像1（原始图像）

import numpy as np
import cv2
import vvdutils as vv


if __name__ == '__main__':
        
    img = vv.cv_rgb_imread('test.jpeg')          # queryImage
    src_pts = np.float32([
                            [101, 49],
                            [242, 124],
                            [241, 256],
                            [101, 262]
                        ]).reshape(-1,1,2)

    dst_pts = np.float32([ 
                            [100, 100],
                            [700, 100],
                            [700, 400],
                            [100, 400]
                        ]).reshape(-1,1,2)

    M, mask = cv2.findHomography(src_pts, dst_pts, cv2.RANSAC, 5.0)
    matchesMask = mask.ravel().tolist()

    dst = cv2.warpPerspective(img, M, [900, 700])
    vv.PIS(dst)
    pass