本文最后更新于:2024年5月7日 下午
本文继续 大神 的 Transformer 介绍,进入第四篇 —— Transformer 的细节。
问题
经过之前几篇的实践, 当你把这个模型应用到任务当中时,你会发现,这并不能达到论文中所描述的 SOTA 结果。 这篇文章中,我们聊一聊那些在论文中一笔带过的 tricks,这些 tricks 让 Transformer 达到了真正的高度。
-
Transformer 的输入,文本的 Tokenize 优化方法
-
Input 和 Output Embedding
-
Positional Encoding 背后的思考
-
- 为什么位置信息的嵌入使用的是 sum(相加) 的方式而不是 concat(串联) 的方式?
- 位置信息到达上层之后,不会消失吗?
- 为什么同时使用正弦和余弦?
-
为什么要增加残差网络?
-
MultiHead Attention 捕获到了什么?
-
为什么要增加 NormLayer,怎么不是 BatchLayer?
-
FFN 增加到这里做什么用的,可不可以去掉?
Transformer 的输入,文本的 Tokenize 怎么做?
通常来讲,我们在做自然语言处理任务的时候,会把文本进行分词(tokenize),然后把这些词用 onehot 的形式表示。送到模型里。比如说,如果是操作英文,我们会根据情况把每个词或者是字母分割出来;处理中文的时候,我们会根据情况分割成词或者是字。
但是,在 Transformer 中,提到了一种方法,叫做 byte-pair encoding,这种方法是 wordpiece 方法族中的其中一种。为什么要这么做呢?
其实,主要是从基于 word 和 character 两种方式都会有一些弊端,使用 word 的方式会导致词表很大,并且容易出现 OOV(out of vocabulary) 的问题(目标词不在词典中);而如果使用 character 的方式,会导致序列过长,并且丧失掉语言中以词汇为单元的特征。两种都不是特别的理想,wordpiece 方法的思路就是,在 character 和 word 之间找到一种中间的分割方式,从而能够最大可能的利用这两种方式的优点。而 BPE 就是其中的一种,BPE 的思路是基于语料频率来进行统计,把出现最多的子词作为切分的依据。
我们来看下代码,到底是怎么做的?
1 | |
接着,统计字典中,每个 character 对出现的频率。
1 | |
使用 get_pair_stats 处理上面的词典。
1 | |

上面这张图就是统计出来的结果,我们能看到 l 和 o 共出现了 7 次,o 和 w 共出现了 7 次,加下来我们要对出现最多的进行合并,比如上面的例子,就是让 e 和 s 变成一个字词 es。
1 | |
我们接着使用这个方法处理上面的统计结果。
1 | |

接下来,就是反复的经过这两步统计、合并,直到最终形成的词典的大小符合我们所设定的大小,就完成了整个 BPE 的过程。
之后,在我们转换输入的时候,就是按照 BPE 生成的词典来进行转换。这种方式能够比较好的继承两种方法的优点。
Input 和 Output Embedding
接下来,就是把上面的 BPE 通过一层 Embedding 把 onehot 投射到一个向量空间里,在这个这个向量空间里,我们通过 BPE 切割出来的子词会通过学习得到一个合适的向量,这两的合适指的是如果他们语义相近、时态相近、语法相近或者是其他的维度的相近,都会在这个向量空间中得到体现。就像下图一样:
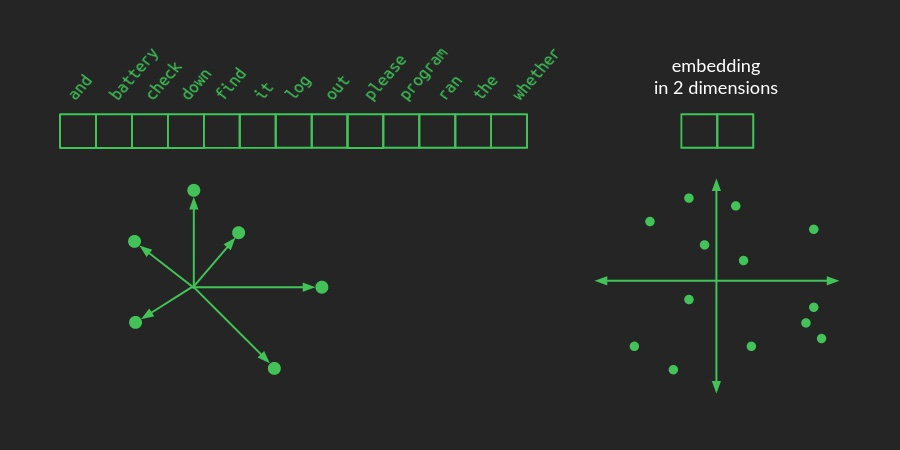
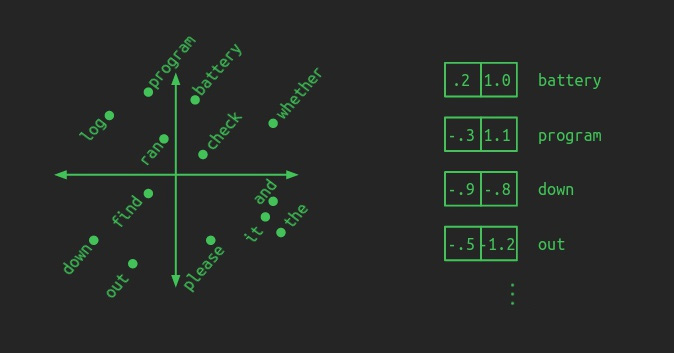
Positional Encoding 背后的思考
接下来,我们要解决之前在讲解 Self-attention 时留下的一个问题,我们的这这些输入在经过 Self-attention 处理时,是放弃了语句的顺序的,这个也很好理解,因为 Self-attention 实质上是根据注意力的权重,重新的计算了 token 的向量,但是我们在注意力的计算中,并没有考虑到顺序的问题。
但是,大家也知道,在自然语言处理中,语言的顺序是非常重要的,比如说“我爱北京”和“北京爱我”,虽然字面上是相同的,通过 Self-attention 计算后也是相同的,但是实质上,它们是有着本质上的差别的。
OK,那接下来就是怎么才能把 token 的位置顺序也建模进去呢?
这里的 Transformer 的思路也很知觉性,就是既然所有的 token 都能用向量空间里面的某个点来表示,那么位置顺序当然也可以用 向量空间里面的一个点来表示。就像下图中展示的一样:
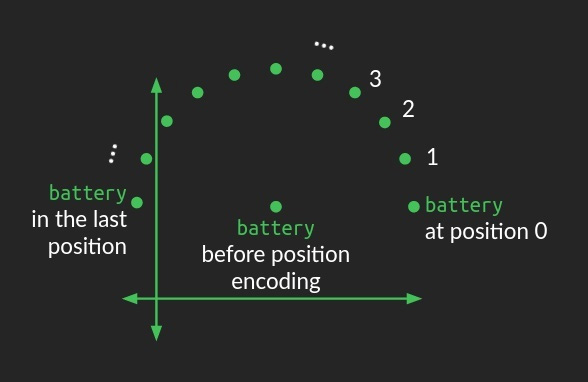
但是,这里很有趣的一点是,作者并没有直接也上一个可学习的参数来学习这些位置的向量信息,而是使用了一个函数进行映射。这里作者应该是考虑到,如果我用可学习的参数来学习位置信息,那么为了能够让模型能够预测,那么在训练阶段,就一定也要见过预测时需要的位置信息。并且,让模型自己去学习位置的编码的信息,这也加大了模型学习的难度,就需要更多的数据,更大的计算量才能够学好位置信息,这在当时的时间点来看,可能不是特别的合适。
所以,我们来看下作者的做法。作者是使用了下面的两个函数,来对不同的位置,直接映射成对应的向量。
$$ \begin{aligned} \mathbf{P E}_{p o s, 2 i} & =\sin \left(p o s /\left(10000 \frac{2 i}{h^{w}}\right)\right) \\ \mathbf{P} \mathbf{E}_{p o s, 2 i+1} & =\cos \left(p o s /\left(10000 \frac{2 i}{h^{w}}\right)\right)\end{aligned} $$- N: 序列的长度
- $ h^{w} $ : 位置/token 向量的维度大小
- pos: 当前 token 的位置 $[0, N-1] $
- $ \mathrm{i}: $ 维度的索引 $ \left[0, h^{w}-1\right] $
上面两个公式,是针对偶数维度索引 2i 和奇数维度索引 2i+1,比如说,我们的位置/token 向量的维度大小为 4,那我们计算不同位置的向量的方式就是这样:
$$
\left[\sin \left(p o s / 10000^{\frac{2 * 0}{4}}\right), \cos \left(p o s / 10000^{\frac{2 * 0}{4}}\right), \sin \left(p o s / 10000^{\frac{2 * 1}{4}}\right), \cos \left(p o s / 10000^{\frac{2 * 1}{4}}\right)\right]
$$
估计更让人觉得神奇的是,为什么上面这个公式就能够表示位置呢?
我们先知觉的使用热力图的方式来理解下,把上面的公式通过热力图画出来如下:
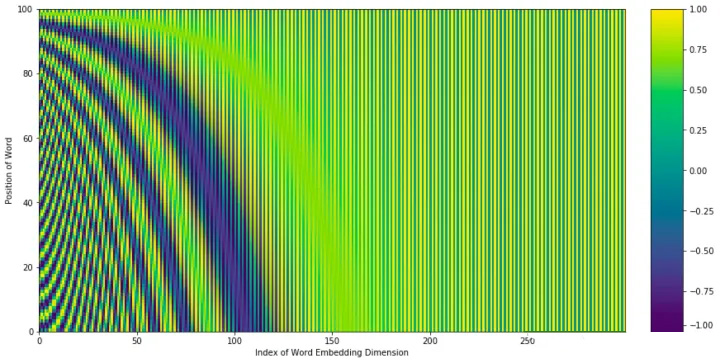
这张图的 x 轴是不同维度的索引值, y 轴是位置,但是好像这么看还是看不来有什么门道。接下来,我们要在这张图上按照 X 轴和 Y 轴进行切片,能得到下面这张图:
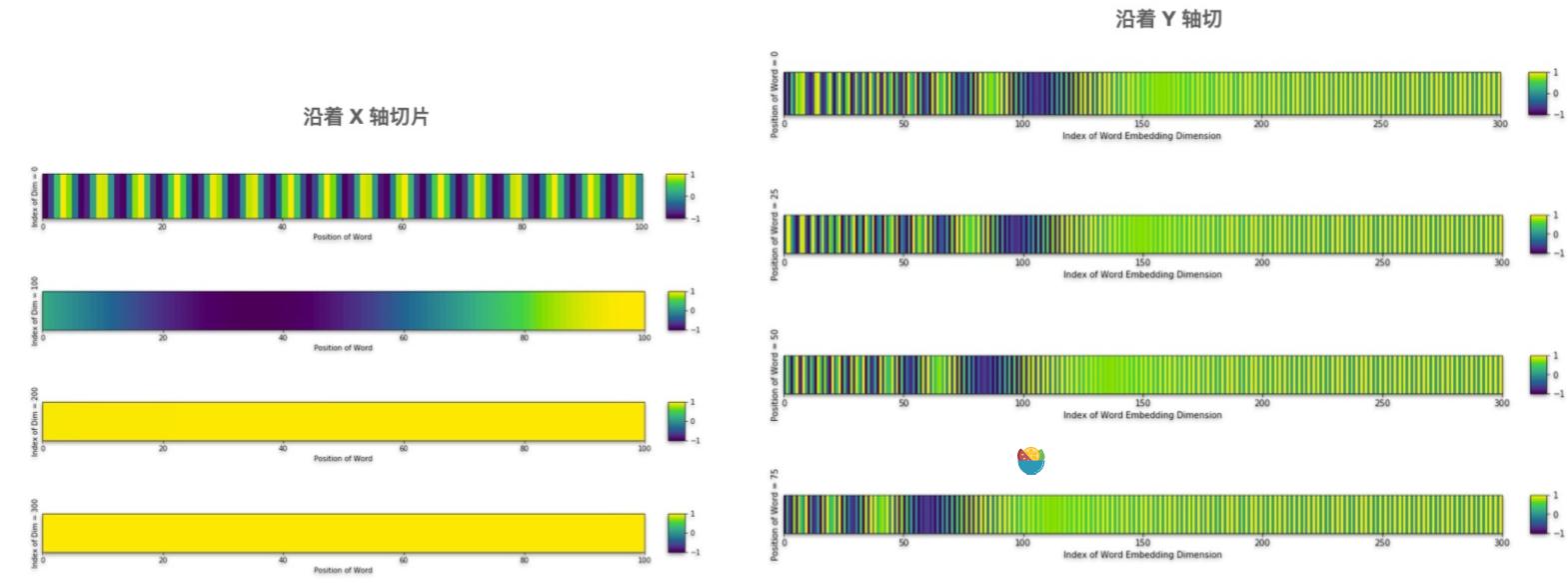
- X 轴切代表:某一个位置在不同维度上的数值;
- Y 轴切表示:同一个维度,不同位置上的数值。
通过这两个切片,我们能发现两个规律:
- 每个位置的编码信息都不同(左图);
- 低维度的数值在不同的位置区别比较大,但是在高纬度的数值变化较小,基本是一样的。
这样表示的好处是,既能够给每个位置不同的编码,又高纬度的信息一致,与原来的 token 向量相加时,不会完全覆盖掉这部分信息,这里面所蕴含的含义有点像是说每个 token 编码是由
上面这些只能说是从直觉上的,在论文中作者有提到:
“We chose this function because we hypothesized it would allow the model to easily learn to attend by relative positions, since for any fixed offset k, $P E_{p o s+k} $ can be represented as a linear function of $P E_{\text {pos }} $ .”
我们选择这个函数是因为我们假设它可以让模型很容易地通过相对位置来学习,因为对于任何固定偏移,都可以表示为线性函数。
但这是为什么呢?接下来我们来证明 Transformer 中位置编码中相对位置之间的线性关系。
问题定义
假设一个矩阵包含$ d_{\text {model }} $ 维列向量 $E_t$ ,这个向量长度为 $n$,在输入序列中编码位置 为 $ t $ 。
$$ e(t)=\boldsymbol{E}_{t,:}:=\left[\begin{array}{c}\sin \left(\frac{t}{f_{1}}\right) \\ \cos \left(\frac{t}{f_{1}}\right) \\ \sin \left(\frac{t}{f_{2}}\right) \\ \cos \left(\frac{t}{f_{2}}\right) \\ \vdots \\ \sin \left(\frac{t}{\frac{f_{\text {model }}}{2}}\right) \\ \cos \left(\frac{t}{f_{\frac{d_{\text {model }}}{}}^{2}}\right)\end{array}\right] $$其中频率为 :
$$
f_{m}=\frac{1}{\lambda_{m}}:=10000^{\frac{2 m}{d_{\text {model }}}}
$$
接下来证明存在某种线性变换 $ \boldsymbol{T}^{(k)} \in \mathbb{R}^{d_{\text {model }} \times d_{\text {model }}} $ 存在,能够保留序列中任何有效位置 $ t \in{1, \ldots, n-k} $ 的任何位置偏移 $ k \in{1, \ldots, n} $ 。
推导
接下来,我们要找到不依赖于 $ \mathrm{t} $ 的 $ \boldsymbol{T}^{(k)} $
$$ \boldsymbol{T}^{(k)}=\left[\begin{array}{cccc}\boldsymbol{\Phi}_{1}^{(k)} & \mathbf{0} & \cdots & \mathbf{0} \\ \mathbf{0} & \boldsymbol{\Phi}_{2}^{(k)} & \cdots & \mathbf{0} \\ \mathbf{0} & \mathbf{0} & \ddots & \mathbf{0} \\ \mathbf{0} & \mathbf{0} & \cdots & \boldsymbol{\Phi}_{\frac{d_{\text {model }}}{2}}^{(k)}\end{array}\right] $$其中 0 表示 $ 2 \times 2 $ 的零矩阵和 $ \frac{d_{\text {model }}}{2} $ 位于主对角线上的转置旋转矩阵 $ \boldsymbol{\Phi}^{(k)} $
$$ \boldsymbol{\Phi}_{m}^{(k)}=\left[\begin{array}{cc}\cos \left(r_{m} k\right) & -\sin \left(r_{m} k\right) \\ \sin \left(r_{m} k\right) & \cos \left(r_{m} k\right)\end{array}\right]^{\top} $$波长 $ r_{m} $ (不要与编码波长 $ \lambda_{m} $ 混淆)。
我们要证明的是:
$$ \underbrace{\left[\begin{array}{cc}\cos \left(r_{m} k\right) & \sin \left(r_{m} k\right) \\ -\sin \left(r_{m} k\right) & \cos \left(r_{m} k\right)\end{array}\right]}_{\boldsymbol{\Phi}_{m}^{(k)}}\left[\begin{array}{c}\sin \left(\lambda_{m} t\right) \\ \cos \left(\lambda_{m} t\right)\end{array}\right]=\left[\begin{array}{l}\sin \left(\lambda_{m}(t+k)\right) \\ \cos \left(\lambda_{m}(t+k)\right)\end{array}\right] $$我们需要依赖 $ \lambda $ 和 $ k $ 来确定 $ r $ ,并且同时消除 $ t $ , 可以使用三角函数中的和角公式来解决:
$$ \begin{aligned} \sin (\alpha+\beta) & =\sin \alpha \cos \beta+\cos \alpha \sin \beta \\ \cos (\alpha+\beta) & =\cos \alpha \cos \beta-\sin \alpha \sin \beta\end{aligned} $$展开后发现:
$$
\begin{array}{l}\lambda k=r k \ \lambda t=\lambda t\end{array}
$$
即有 : $r=\lambda$
带回旋转矩阵:
$$ \boldsymbol{\Phi}_{m}^{(k)}=\left[\begin{array}{cc}\cos \left(\lambda_{m} k\right) & \sin \left(\lambda_{m} k\right) \\ -\sin \left(\lambda_{m} k\right) & \cos \left(\lambda_{m} k\right)\end{array}\right] $$其中 $ \lambda_{m}=10000^{\frac{-2 m}{d_{m o d e l}}} $ 。有了它, $ \boldsymbol{T}^{(k)} $ 完全指定并仅依赖于 $ m 、 d_{\text {model }} $ 和 $ k $ 。序列中的 位置 $ t $ 不是一个参数(证明完毕)。
几个可能会困扰你的问题
也是经常被拿来做面试题的
1. 为什么位置信息的嵌入使用的是 sum(相加) 的方式而不是 concat(串联) 的方式?
我找不到这个问题的任何理论上的解释。由于求和(与串联相反)节省了模型的参数,因此可以将最初的问题改为“向单词添加位置嵌入是否可行?”。我的答案是,不一定就有用!
如果我们还记得上面的位置编码的直觉的感受,我们会发现只有整个向量的前几个维度用于存储和位置有关的信息。由于 Transfomer 中的参数是从头开始训练的,因此自动学习的参数可能会将捕获到的语义的信息存储到后面的维度中,以避免干扰位置编码。
基于同样的原因,我认为 Transformer 可以自动的将单词的语义与其位置信息分开。而且,没有理由将独立表示当成是一种优势,也许模型能够融合这些特征得到一种更有意义的特征。
2. 位置信息到达上层之后,不会消失吗?
幸运的是,Transformer 架构使用了 Residula 连接的方式。因此,来自模型输入的信息(包含位置嵌入)可以有效地传播到处理更复杂交互的其他层。
3. 为什么同时使用正弦和余弦?
我个人认为,只有同时使用正弦和余弦,我们才能将正弦(x+k)和余弦(x+k)表示为 $\sin(x)$ 和 $\cos(x)$ 的线性变换。你不能对单一的正弦或余弦做同样的事情。
最后附上 Positional Encoding 的代码:
1 | |
以上就是 Transformer 的输入部分内容,接下来就开始进入到 Transformer Encoder 的结果部分,这部分我们主要探讨,为什么是要用这些结构呢?每个结构起作用的方式又是什么呢?
这个结构里,主要涉及到了几个重要的部分
- Residual Network (Skip Connection)
- Multi-Head Attention
- Add & Norm
- Feed Forward
为什么要增加残差网络
大家能够看到,在整个 Transformer 的结构中,基本上在所有的基础组件处理后,都增加了一个残差网络(或者叫做跳接网络),这是为什么呢?大家还记得我们上文在聊 Positional Encoding 的时候,有说到位置信息之所以能够向上传递有个很重要的原因就是通过残差网络,信息可以直接通过,不需要做其他的处理,这样位置信息得到了很好的传递。
接下来我们来说一下残差网络的作用,这里主要是有两个作用(也是经常被拿来做面试题的):
首先,它们有助于保持梯度的平滑,这对反向传播有很大帮助。通常我们认为,注意力是一个过滤器,这意味着当它正常工作时,它会阻止大部分试图通过它的东西。这样做的结果是,如果许多输入碰巧落入阻塞的通道中,那么许多输入的微小变化可能不会对输出产生太大的变化。这会在平坦的梯度上产生死点,但它仍然没有靠近谷底。这些鞍点和脊是反向传播的一个非常大的障碍。残差网络有助于消除这些问题。在有注意力的情况下,即使所有权重都为零,所有输入都被阻塞,残差连接也会将输入的一个副本值添加到结果中,并确保任何输入的微小变化仍会对结果产生显著的变化。这可以防止梯度下降过程中无法得到一个好的拟合结果的困境。
自从 ResNet 图像分类器问世以来,由于残差连接可以显著提高性能,因此它现在变得非常流行。现在它基本上已经是神经网络架构中的标准组件。我们可以通过比较有连接和没有连接的网络来看到残差连接的效果,如下图,这里对比了具有或不具有残差连接的 ResNet 网络。当使用残差连接时,损失函数梯度的斜率要适中且均匀得多。
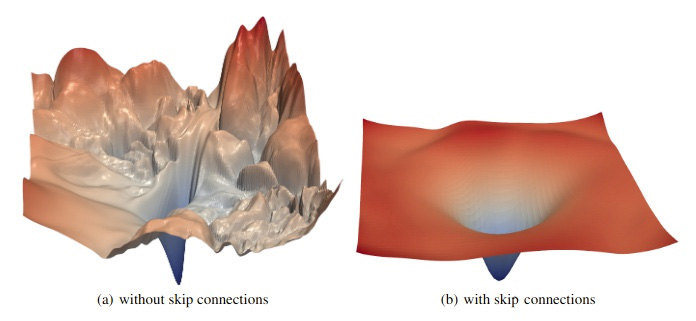
跳接的第二个目的是专门为了 Transformer 结构而添加的,为了保留原始的输入序列的信号。在 Transformer 中,即使已经有很多注意力机制,也不能保证一个单词会注意到它自己的位置和周围的单词。注意力过滤器可能会完全忘记最近的单词,转而关注所有可能相关的早期单词。残差连接通过获取原始单词并手动将其添加到向下传递的信号中,这样就不会删除或者是忘记它,这给 Transformer 结构增加了信号传递的稳定性,这可能是 Transformer 在许多不同的序列任务中表现良好的原因之一。
参考资料
文章链接:
https://www.zywvvd.com/notes/study/deep-learning/transformer/transformer-intr/transformer-intr-4/
“觉得不错的话,给点打赏吧 ୧(๑•̀⌄•́๑)૭”

微信支付

支付宝支付