本文最后更新于:2024年5月7日 下午
经过多年发展,深度学习中出现多种常用的归一化层,主要包括 BatchNorm、LayerNorm、GroupNorm、InstanceNorm 等,本文记录相关内容。
归一化
归一化的目的是将不同的数据分布强行变换到一个相对稳定的分布空间上来,在深度学习中
数据归一化通常有以下几个好处:
- 缩小特征间的差异:当数据分布范围很大时,数值较大的特征会对数值较小的特征产生权重上的优势,通过归一化可以减少这种影响。
- 加速学习算法:一些学习算法(如梯度下降)在处理特征数量级差异很大的数据时,学习速率会受到影响,归一化后可以加快学习速率。
- 避免数值问题:在某些数学公式或运算中,特征的数值如果过大或过小,可能会导致计算上的问题,如梯度消失或爆炸。
在深度学习中近几年出现了几种归一化层:
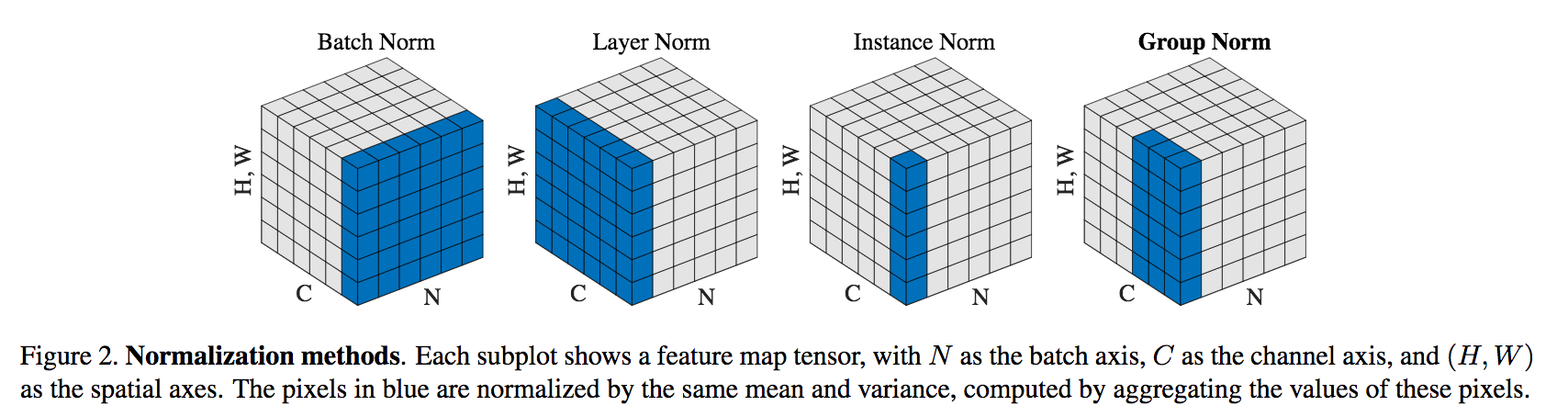
BatchNorm(2015年)、LayerNorm(2016年)、InstanceNorm(2016年)、GroupNorm(2018年);
将输入的图像shape记为[N,C,H,W],这几个方法主要区别是:
- BatchNorm:batch方向做归一化,计算NHW的均值,对小batchsize效果不好;
(BN主要缺点是对batchsize的大小比较敏感,由于每次计算均值和方差是在一个batch上,所以如果batchsize太小,则计算的均值、方差不足以代表整个数据分布) - LayerNorm:channel方向做归一化,计算CHW的均值;
(对RNN作用明显) - InstanceNorm:一个batch,一个channel内做归一化。计算HW的均值,用在风格化迁移;
(因为在图像风格化中,生成结果主要依赖于某个图像实例,所以对整个batch归一化不适合图像风格化中,因而对HW做归一化。可以加速模型收敛,并且保持每个图像实例之间的独立。) - GroupNorm:将channel方向分group,然后每个group内做归一化,算(C//G)HW的均值;这样与batchsize无关,不受其约束。
BatchNorm
原始论文:https://arxiv.org/abs/1502.03167
BN对各种极端的超参数都有很强的适应能力。在训练的过程中使用BN我们完全可以使用较大的学习率加快收敛速度,而且不会影响模型最终的效果。BN通过将每一层网络的输入进行normalization,保证输入分布的均值与方差固定在一定范围内,并在一定程度上缓解了梯度消失,加速了模型收敛;并且BN使得网络对参数、激活函数更加具有鲁棒性,降低了神经网络模型训练和调参的复杂度;最后BN训练过程中由于使用mini-batch的mean/variance作为总体样本统计量估计,引入了随机噪声,在一定程度上对模型起到了正则化的效果。
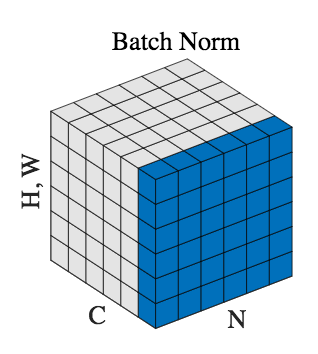
在 N, H, W 三个维度上计算均值和标准差:
$$
y=\frac{x-E[x]}{\sqrt{Var[x]+\epsilon}}\gamma+\beta\quad
$$
其中 $x$ 表示某个通道的数据: $N\times H\times W$
Torch 实现
1 | |
- num_features:输入的特征数,该期望输入的大小为$N \times C [\times L]$;
- eps: 为保证数值稳定性(分母不能趋近或取0),给分母加上的值。默认为1e-5;
- momentum: 动态均值和动态方差所使用的动量,默认为0.1;
- affine: 布尔值,当设为true,给该层添加可学习的仿射变换参数;
- track_running_stats:布尔值,当设为true,记录训练过程中的均值和方差。
实验说明
以 2D 数据为例
- 示例程序
1 | |
输出:
1 | |
有效性的原因
原论文《Batch Normalization:Accelerating Deep Network Training by Reducing Internal Covariate Shift》中,BN的提出是为了解决Internal Covariate Shift (ICF),即在深层网络训练的过程中,由于网络中参数变化而引起内部结点数据分布发生变化的这一过程被称作Internal Covariate Shift。假如我们要训练一个神经网络分类器,我们从训练数据中拿到两个明显分布不同的两个batch。当我们用这两个batch分别去训练神经网络的时候,就会由于训练batch分布的剧烈波动导致收敛速度慢,甚至是神经网络性能的下降。这就是在输入数据上的Covariate shift。通常我们可以通过增大batch的大小,并充分对数据进行shuffle来保证每个batch的分布尽量接近原始数据的分布,从而减少Covariate shift带来的负面影响。
论文《How Does Batch Normalization Help Optimization?》从理论和实验出发详细分析了BN的作用机理。最终的结论是减去均值那一项,有助于降低神经网络梯度的 Lipschitz约束常数,而除以标准差的那一项,更多的是起到类似自适应学习率的作用,使得每个参数的更新更加同步,而不至于对某一层、某个参数过拟合。
LayerNorm
原始论文:https://arxiv.org/abs/1607.06450
在 transformer 中一般采用LayerNorm,LayerNorm也是归一化的一种方法,与BatchNorm不同的是它是对每单个batch进行的归一化,而 batchnorm 是对所有batch一起进行归一化的
在单个样本的 C, H, W 三个维度中的若干维度上计算均值和标准差,方法简单不需要累计计算均值和方差,来一个算一个就完了:
$$
y = \frac{x - E[x]}{\sqrt{Var[x] + \varepsilon}} \cdot \gamma + \beta
$$
Torch 实现
官方文档:https://pytorch.org/docs/stable/generated/torch.nn.LayerNorm.html
1 | |
-
normalized_shape:归一化的维度,int(最后一维)list(list里面的维度)
-
eps:加在方差上的数字,避免分母为0
-
elementwise_affine:bool,True的话会有一个默认的affine参数
elementwise_affine就是公式中的 $\gamma$ 和 $β$,前者开始为1,后者为0,二者均可学习随着训练过程而变化
-
bias:如果设置为 False,图层将不会学习附加偏置项(只有当 elementwise _ affine 为 True 时才相关)。

实验说明
示例一
- 示例代码
1 | |
- 输出
1 | |
上述过程归一化了单个样本的 N, X, Y 三个维度的数据
示例二
- 示例代码
1 | |
- 输出
1 | |
过程中仅对最后两个维度 X, Y 进行了局部归一化,事实上完成了 InstanceNorm 的工作,如果需要,也可以仅对最后一个维度进行归一化。
InstanceNorm
nstance Normalization (InstanceNorm) 是一种在计算机视觉任务中用于图像风格转移和生成对抗网络(GANs)的归一化技术。与批量归一化(Batch Normalization, BN)和层归一化(Layer Normalization, LN)类似,InstanceNorm 的目的是对数据进行归一化处理,以加速模型的训练和改善性能。
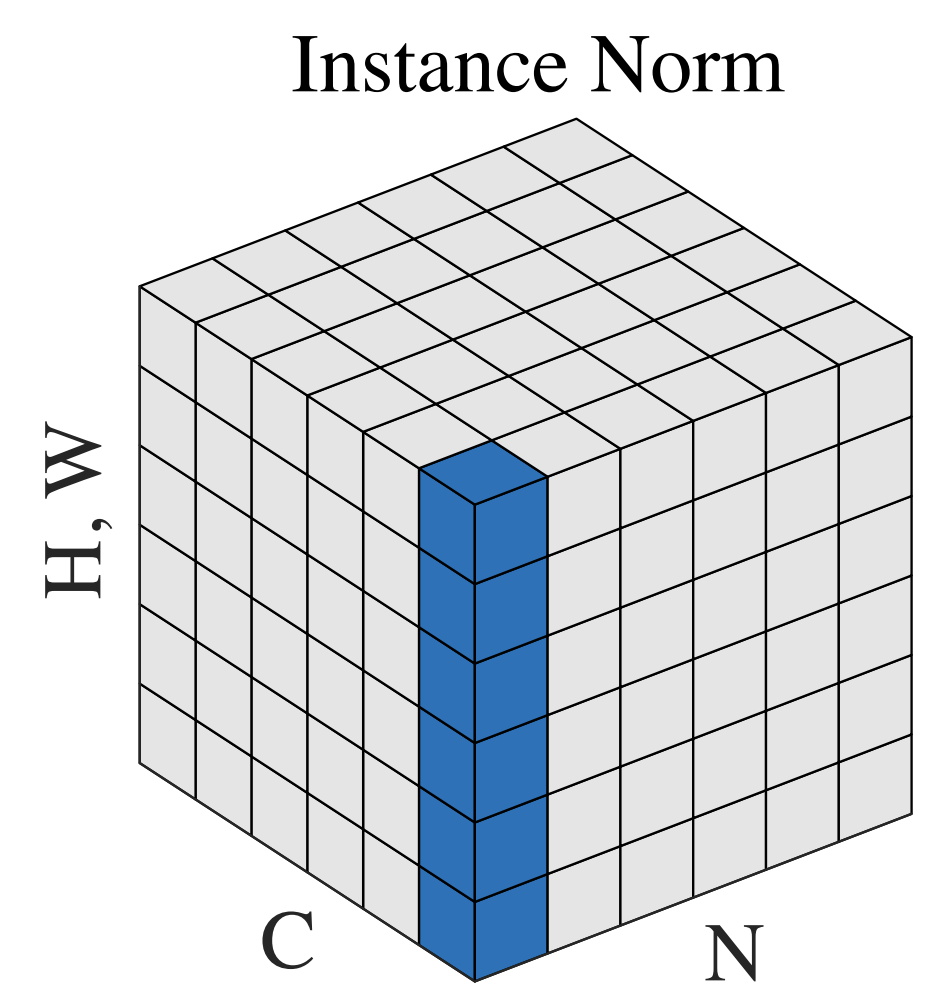
InstanceNorm 的主要思想是对于每个图像样本(而不是整个批次或单个层中的所有激活)独立地计算其均值和方差,并对每个通道(channel)进行归一化。这意味着对于每个样本的每个通道,InstanceNorm 会减去该通道的均值并除以标准差。
 $$
y = \frac{x - E[x]}{\sqrt{Var[x] + \varepsilon}} \cdot \gamma + \beta
$$
$$
y = \frac{x - E[x]}{\sqrt{Var[x] + \varepsilon}} \cdot \gamma + \beta
$$
Torch 实现
官方文档:https://pytorch.org/docs/stable/generated/torch.nn.InstanceNorm1d.html#torch.nn.InstanceNorm1d
1 | |
-
num_features:Channel 维度特征数量
-
eps:加在方差上的数字,避免分母为0
-
momentum: 动量,$x_{new}=(1−momentum)×\hat x+momentum×x_t$, 其中 $\hat x$ 是估计量,$x_t$ 是当前观测值,默认0.1
-
affine:bool,当设置为 True 时,该模块具有可学习的仿射参数,初始化方式与批量标准化相同。默认值: False。
-
bias:如果设置为 False,图层将不会学习附加偏置项(只有当 elementwise _ affine 为 True 时才相关)。
-
track_running_stats: 如果 track_running_stats 设置为 True,则在训练期间,该层将保持计算出的均值和方差的运行估计值,然后在计算期间使用这些估计值进行归一化。运行估计保持默认动量为0.1。
实验说明
- 示例代码
1 | |
- 输出
1 | |
从结果可以看出,IN 对 X,Y 维度做归一化,也可以用 LayerNorm 实现
GroupNorm
原始论文:https://arxiv.org/abs/1803.08494
Group Normbalization(GN)是一种新的深度学习归一化方式,可以替代BN。
众所周知,BN是深度学习中常使用的归一化方法,在提升训练以及收敛速度上发挥了重大的作用,是深度学习上里程碑式的工作,但是其仍然存在一些问题,而新提出的GN解决了BN式归一化对batch size依赖的影响。
$$
y = \frac{x - E[x]}{\sqrt{Var[x] + \varepsilon}} \cdot \gamma + \beta
$$
BN 层的问题
BN全名是Batch Normalization,见名知意,其是一种归一化方式,而且是以batch的维度做归一化,那么问题就来了,此归一化方式对batch是independent的,过小的batch size会导致其性能下降,一般来说每GPU上batch设为32最合适,但是对于一些其他深度学习任务batch size往往只有1-2,比如目标检测,图像分割,视频分类上,输入的图像数据很大,较大的batchsize显存吃不消。
另外,Batch Normalization是在batch这个维度上Normalization,但是这个维度并不是固定不变的,比如训练和测试时一般不一样,一般都是训练的时候在训练集上通过滑动平均预先计算好平均-mean,和方差-variance参数,在测试的时候,不在计算这些值,而是直接调用这些预计算好的来用,但是,当训练数据和测试数据分布有差别是时,训练机上预计算好的数据并不能代表测试数据,这就导致在训练,验证,测试这三个阶段存在inconsistency。
既然明确了问题,解决起来就简单了,归一化的时候避开batch这个维度是不是可行呢,于是就出现了layer normalization和instance normalization等工作。
GN 为何有效
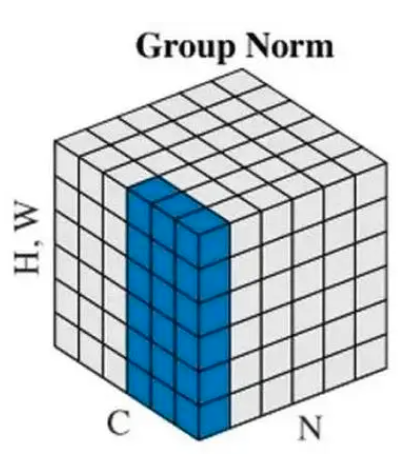
GN介于LN和IN之间,其首先将channel分为许多组(group),对每一组做归一化,及先将feature的维度由[N, C, H, W]reshape为[N, G,C//G , H, W],归一化的维度为[C//G , H, W],事实上,GN的极端情况就是LN和I N,分别对应G等于1和G等于C
传统角度来讲,在深度学习没有火起来之前,提取特征通常是使用SIFT,HOG和GIST特征,这些特征有一个共性,都具有按group表示的特性,每一个group由相同种类直方图的构建而成,这些特征通常是对在每个直方图(histogram)或每个方向(orientation)上进行组归一化(group-wise norm)而得到。而更高维的特征比如VLAD和Fisher Vectors(FV)也可以看作是group-wise feature,此处的group可以被认为是每个聚类(cluster)下的子向量sub-vector。
从深度学习上来讲,完全可以认为卷积提取的特征是一种非结构化的特征或者向量,拿网络的第一层卷积为例,卷积层中的的卷积核filter1和此卷积核的其他经过transform过的版本filter2(transform可以是horizontal flipping等),在同一张图像上学习到的特征应该是具有相同的分布,那么,具有相同的特征可以被分到同一个group中,按照个人理解,每一层有很多的卷积核,这些核学习到的特征并不完全是独立的,某些特征具有相同的分布,因此可以被group。
导致分组(group)的因素有很多,比如频率、形状、亮度和纹理等,HOG特征根据orientation分组,而对神经网络来讲,其提取特征的机制更加复杂,也更加难以描述,变得不那么直观。另在神经科学领域,一种被广泛接受的计算模型是对cell的响应做归一化,此现象存在于浅层视觉皮层和整个视觉系统。
作者基于此,提出了组归一化(Group Normalization)的方式,且效果表明,显著优于BN、LN、IN等。
GN的归一化方式避开了batch size对模型的影响,特征的group归一化同样可以解决$Internal$ $Covariate$ $Shift$的问题,并取得较好的效果。
Torch 实现
1 | |
- num_groups : 要将通道分隔成的组的数目
- num_channels : 预期输入的通道数目
- eps : 增加到数值稳定性分母的值。默认值: 1e-5
- affine :一个布尔值,当设置为 True 时,该模块具有可学习的每通道仿射参数,初始化为1(用于权值)和0(用于偏差)。默认值: True。
实验说明
- 示例代码
1 | |
- 输出
1 | |
- 可以看到手动计算的结果与 gn 层输出一致,实现原理是正确的。
参考资料
- https://zhuanlan.zhihu.com/p/679215898
- https://arthurdouillard.com/post/normalization/
- https://zhuanlan.zhihu.com/p/87117010
- https://proceedings.neurips.cc/paper_files/paper/2018/file/905056c1ac1dad141560467e0a99e1cf-Paper.pdf
- https://pytorch.org/docs/stable/generated/torch.nn.LayerNorm.html
- https://blog.csdn.net/weixin_41978699/article/details/122778085
- https://zhuanlan.zhihu.com/p/152232203
- https://pytorch.org/docs/stable/generated/torch.nn.InstanceNorm1d.html#torch.nn.InstanceNorm1d
- https://arxiv.org/abs/1803.08494
- https://zhuanlan.zhihu.com/p/35005794
文章链接:
https://www.zywvvd.com/notes/study/deep-learning/layer/norm-layer/norm-layer/
“觉得不错的话,给点打赏吧 ୧(๑•̀⌄•́๑)૭”

微信支付

支付宝支付