膨胀卷积

本文最后更新于：2024年5月28日上午

Dilated conv，中文叫做空洞卷积或者膨胀卷积，起源于语义分割，本文记录相关内容。

背景

膨胀卷积是为解决语义分割任务而提出的。因为深度学习的蓬勃发展，其也被迁移应用于语义分割领域。当时的SOTA方法多是基于卷积神经网络，但卷积神经网络当初是为图像分类任务而设计的。语义分割作为一种稠密预测（Dense Prediction）任务——语义分割是像素级的分类任务，与图像分类具有结构上的不同。这里的不同指的应该是，图像分类的网络只需输出相应的物体类别的概率，而语义分割网络则需要输出与原图像大小相同的图像。

图像分类任务为了获取足够的感受野（感受野的概念会在下文进行讲解），都会通过池化层或者大步长的卷积对图像和特征图进行下采样的操作，这样就减小了图像或者特征图的分辨率，这与语义分割的输出要求是相违背的。当时解决此问题主要有两种办法：

对图像或特征图进行上采样，恢复因为获取感受野进行下采样而丢失的分辨率
将输入图像缩放到多种尺寸并输入网络，结合多尺度图像得到最终的预测结果

但膨胀卷积的作者对此两种方法提出疑问：网络中的下采样层对于语义分割任务来说真的是必要的吗？多尺度图像的输入是必要的吗？有没有什么办法可以在不改变图像分辨率的前提下获取足够的感受野，使得网络关注多尺度的上下文语义信息？

基于以上疑问，作者受到小波变换领域的膨胀概念，提出了膨胀卷积，并将其做成即插即用的模块，放入卷积神经网络中。如图1所示，经测试，取得了不错的效果。

膨胀卷积，顾名思义，是经过膨胀设计的卷积运算。

可以看出，膨胀卷积的卷积核是在普通卷积核的基础上扩大了尺寸，但是真正参与运算的卷积核单元没有变化（图中只有蓝色方块才是参与运算的单元，无色小方块中的元素用0填充。左半部分的普通卷积核尺寸为３×3，右半部分卷积核尺寸为５×５，但右半部分深蓝色的参与运算的元素依然是９ [3×3] 个），看到这里大家应该知道膨胀卷积是什么样的了。

普通卷积

膨胀卷积

设计原理

可以看出，膨胀卷积其实是通过扩大卷积核尺寸的方式来增大感受野，同时既没有增大计算量，也没有降低特征图的分辨率。

膨胀卷积有一个超参数：膨胀因子S，通过膨胀因子我们可以控制卷积核的膨胀程度，上图中的膨胀因子为2。膨胀因子是如何控制卷积核的膨胀程度的呢？
$$
K_c=S×(K_o-1)+1K
$$
参数含义：

$K_c:K $: 普通卷积核通过膨胀设计后的卷积核尺寸
$K_o$: 普通卷积核尺寸

上图中，普通卷积核尺寸3×3，S SS为2，那么膨胀之后的卷积核尺寸为5×5。

膨胀卷积核元素之间的间隔 = S-1，图中 $S=2$，行列元素间隔各为1。

感受野

感受野 是影响深度神经网络性能的重要因素之一。所以在平时深度神经网络的设计中要注意各层特征图的感受野，以确保在当前层能获得适合所解决任务需要的感受野大小，即特征图中包含了足够多原图的语义信息，从而发挥出深度神经网络的最佳性能。

感受野有比较科学的计算公式：
$$
RF_{l+1}=RF_l+(k-1)*S_l
$$

参数含义：

$RF_{l+1}$: 第 $l+1$层的感受野
$RF_{l}$ : 第 $l$ 层的感受野
$k$: 第 $l+1$ 的卷积核尺寸
$S_l$: 前 $l$ 层的步长之积

注意: 当前层的步长并不影响当前层的感受野。

膨胀卷积的感受野的计算方式

$F_1 ,F _2 ,F _3$ 分别是第1，2，3层特征图。$ F_1,F_2,F_3$ 是级联形式，即$ F_1$ 是由原图得到的，$F_2$ 是由 $F_1$ 得到的，$F_3$ 是由 $F_2$ 得到的。每层特征图均采用步长为1的方式计算得到。根据上边计算感受野的公式可知：

$F_1$ 的感受野 = $3+(3+1)*(2^0-1)=3$，3×3 注意：原图的感受野为1
$F_2$ 的感受野= $3+(3+1)*(2^1-1)=7$ ，7×7
$F_3$ 的感受野= $3+(3+1)*(2^1-1)=15$，15×15

作者在论文中给出的计算公式：
$$
RF_{i+1}=(2^{i+2}-1)×(2{i+2}-1)
$$

$RF_{i+1}$：第 $ i+1$ 层特征图的感受野

膨胀卷积的优缺点

优点

使得输出更为稠密，适应语义分割任务；

避免了使用 down-sampling 这样的特性；

在不降低分辨率的情况下，增大感受野。

缺点

gridding problem，如果我们叠加多个相同的膨胀卷积，会发现感受野中有很多像素没有利用上（感受野的方阵中只有蓝色和红色方块参与计算，白色方块使用零填充，相当于没有参与运算），出现大量空洞。此时，会丢失数据之间的连续性及完整性，不利于学习。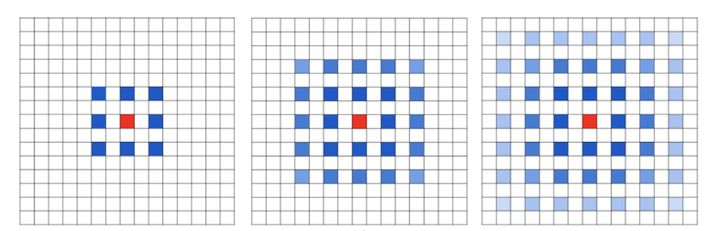
长距离的信息有时是不相关的，膨胀卷积扩大了感受野，因此可以取得长距离信息（在图像中这是有利于大目标分析的），但是有些长距离信息和当前点是完全不相关的，会影响数据的一致性（对于小目标不太友好）。

膨胀卷积的改进

针对以上缺点，图森未来的研究人员对膨胀卷积进行了改进，并提出了Hybrid Dilated Convolution（HDC）。HDC主要有三个特性：

叠加卷积的膨胀因子不能有大于1的公约数。比如 [2, 4, 6] 则不是一个好的三层卷积，依然会出现 gridding effect。
膨胀因子可以设计成锯齿状结构，例如 [1, 2, 5, 1, 2, 5] 循环结构。
膨胀因子需要满足以下公式：
$$
M_i=Max(M_{i+1}-2r_i,M_{i+1}-2(M_{i+1}-r_i),r_i)M
$$
参数含义：

$r_i$：第i层的膨胀因子
$M_i$：这i层的最大的膨胀因子

基于Pytorch的代码实现

Pytorch中膨胀卷积和普通卷积共用一个API，只是通过膨胀因子的参数进行区分，膨胀因子设置为1时就是普通卷积。

1	`torch.nn.Conv2d(in_channels, out_channels, kernel_size, stride=1, padding=0, dilation=1, groups=1, bias=True, padding_mode='zeros', device=None, dtype=None)`

参数含义：

in_channels (int) – Number of channels in the input image
out_channels (int) – Number of channels produced by the convolution
kernel_size (int or tuple) – Size of the convolving kernel
stride (int or tuple, optional) – Stride of the convolution. Default: 1
padding (int, tuple or str, optional) – Padding added to all four sides of the input. Default: 0
padding_mode (string, optional) – ‘zeros’, ‘reflect’, ‘replicate’ or ‘circular’. Default: ‘zeros’
dilation (int or tuple, optional) – Spacing between kernel elements. Default: 1
groups (int, optional) – Number of blocked connections from input channels to output channels. Default: 1
bias (bool, optional) – If True, adds a learnable bias to the output. Default: True