异常检测 PatchCore

异常检测在工业检测等场景有重要应用，PatchCore 在 MVTec 数据集中霸榜了很久，本文介绍相关内容。

异常检测

• 异常检测是无监督学习的一种应用场景
• 通过对正常数据建模，获取对正常数据的表示模型
• 该模型在表示异常数据时会有异常的表现，以此描述异常数据

PatchCore

在异常检测算法 MVTec 数据集的 排名：

算法流程

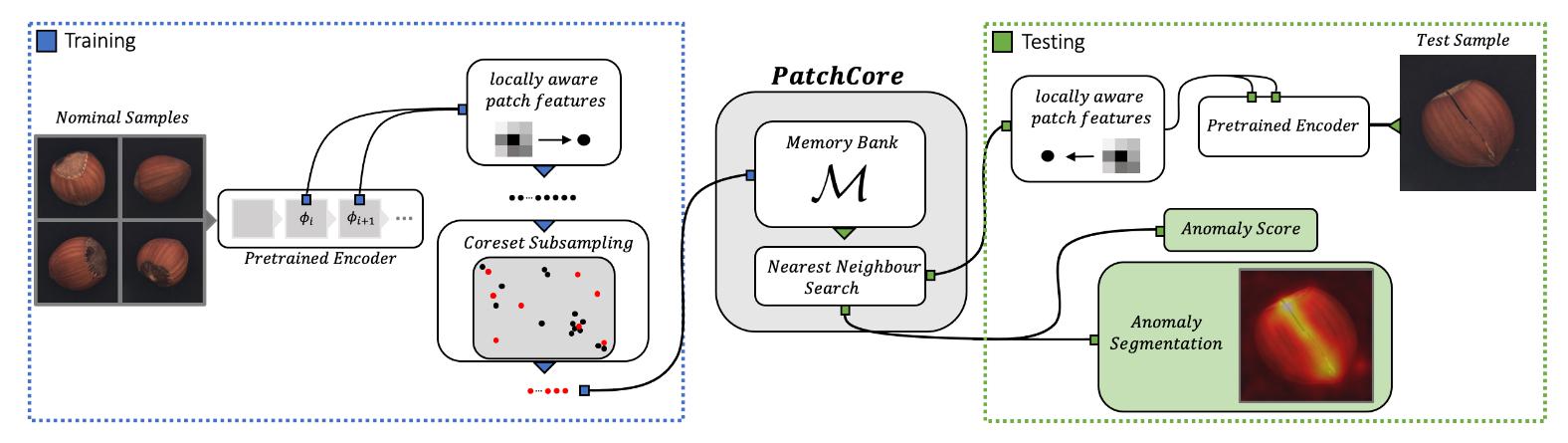
提取特征

特征级别

• 用预训练模型 Backbone 提取图像特征
• 以 Resnet50 为例，原文放弃了局部正常特征数据较少、偏向于分类任务的深层特征，采用第 [2, 3] 层特征作为图像特征

Patch 特征

• 将图像分为 $p\times p$ 的小块提取图像的 patch特征，这个特征带有周围数据的信息

• 以每个 patch 中间位置 $h,w$ 为中心，取边长为 $p$ 的正方形区域

  $$ \begin{aligned} \mathcal{N}_{p}^{(h, w)}=\{(a, b) \mid a& \in[h-\lfloor p / 2\rfloor, \ldots, h+\lfloor p / 2\rfloor] \\ b &\in[w-\lfloor p / 2\rfloor, \ldots, w+\lfloor p / 2\rfloor]\} \end{aligned} $$

• 围绕这些点计算的特征图上的点为

$$ \phi_{i, j}\left(\mathcal{N}_{p}^{(h, w)}\right)=f_{\mathrm{agg}}\left(\left\{\phi_{i, j}(a, b) \mid(a, b) \in \mathcal{N}_{p}^{(h, w)}\right\}\right) $$

• 一幅图像的 Patch 特征集合为：

$$ \mathcal{P} _ {s, p} \left (\phi _ {i, j} \right) = \left\{\phi _ {i, j} \left(\mathcal{N} _ {p} ^ {(h, w)}\right) | h, w \bmod s=0, h < h ^ { *}, w< w^{ *}, h, w \in \mathbb{N}\right\} $$

构建 Memory Bank

Memory Bank

• 将收集到的正常图像 Patch 特征放入 MemoryBank

  $$ \mathcal{M}=\bigcup_{x_{i} \in \mathcal{X}_{N}} \mathcal{P}_{s, p}\left(\phi_{j}\left(x_{i}\right)\right) $$

Reduce memory bank

• 通过稀疏采样在尽可能保持特征表达能力的情况下，使得 MemoryBank 稀疏化（为了加快算法运行速度）

• 在确定目标Bank 特征数量后通过优化以下目标实现稀疏化

  $$ \mathcal{M}_{C}^{*}=\underset{\mathcal{M}_{C} \subset \mathcal{M}}{\arg \min } \max_{m \in \mathcal{M}} \min _{n \in \mathcal{M}_{C}}\|m-n\|_{2} $$

含义为找到一个特征集合 $\mathcal {M}_ {C} $，使得 $\mathcal{M}$ 中任意特征距离 $\mathcal{M}_{C}$ 中最近的特征的距离的最大值最小

• 之后用一些选择特征的策略获取稀疏化 Memory Bank

梳理构建流程

异常检测

• 构建 Memory Bank 相当于使用正常数据进行模型训练、构建
• 之后输入待检测的图像进行异常检测，相当于 infer

infer 流程

• 提取 Patch 特征：

$$ \mathcal{P}\left(x^{test}\right) = \mathcal{P}_{s, p}\left(\phi_{ j}(x^{test})\right) $$

• 对于每个 Patch 特征选择 $\mathcal{M}_{C}$ 中距离最近的特征 $m^*$

$$ \begin{aligned} m^{\text {test }, *}, m^{*} &=\underset{m^{\text {test }} \in \mathcal{P}\left(x^{\text {test }}\right)}{\arg \max } \underset{m \in \mathcal{M}}{\arg \min }\left\|m^{\text {test }}-m\right\|_{2} \\ s^{*} &=\left\|m^{\text {test }, *}-m^{*}\right\|_{2} . \end{aligned} $$

公式 $ \arg \min \left || \mathrm{m}^{\text {test }}-\mathrm{m}\right || $ 计算的是 点 $ \mathrm{m}^{\text {test }} $ 到集合 $ \mathrm{M} $ 的距离，选择距离最远的异常值

距离最远的点为图像的异常值分数

• 文中强调为了提升算法鲁棒性，采用一个公式更新了异常值 $s^*$

$$ s=\left(1-\frac{\exp \left\|m^{\text {test }, *}-m^{*}\right\|_{2}}{\sum_{m \in \mathcal{N}_{b}\left(m^{*}\right)} \exp \left\|m^{\text {test }, *}-m\right\|_{2}}\right) \cdot s^{*} $$

我的理解为：对于特征稀疏的区域倾向于判定为异常，反之给予异常值一定的削减

每个点的异常值拼接起来即可获得图像的异常热力图

原始论文

参考资料

• Towards Total Recall in Industrial Anomaly Detection

文章链接：
https://www.zywvvd.com/notes/study/deep-learning/anomaly-detection/patchcore/patchcore/