异常检测 DeepSVDD

本文最后更新于：2023年12月26日上午

本文记录神经网络用于一分类异常检测的开山工作 —— DeepSVDD。

简介

论文：Deep One-Class Classification
开源代码：https://github.com/lukasruff/Deep-SVDD-PyTorch

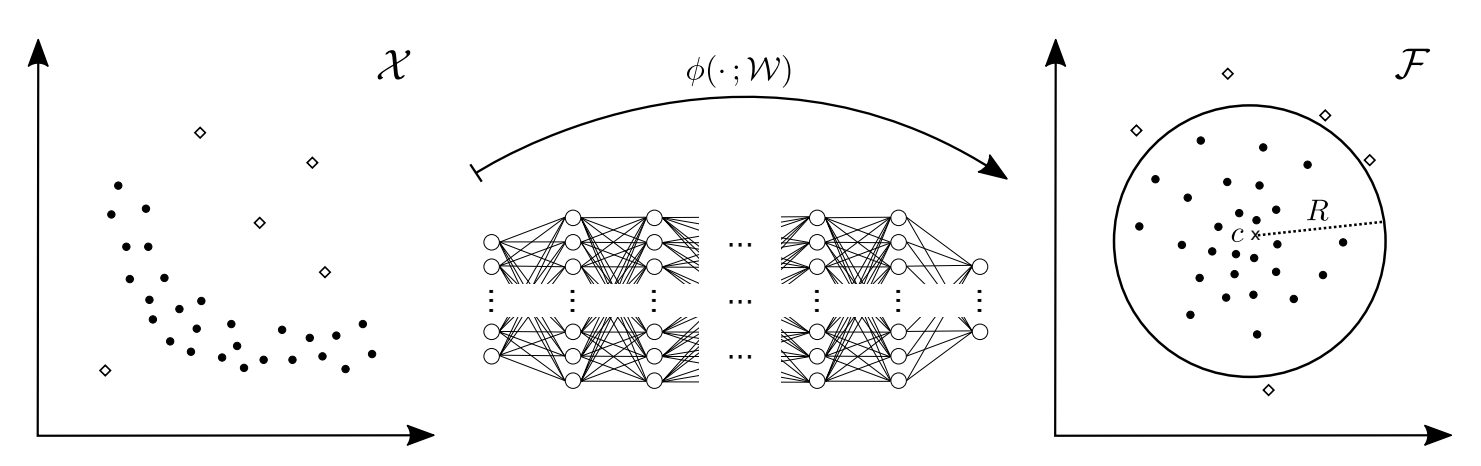
基于核的单分类异常检测方法难以处理高维样本特征而且计算效率低，因此论文中对此类方法进行优化提出了深度 Deep SVDD 模型。主要想法是利用神经网络训练来最小化计算样本特征空间的划分超球面，然后根据球心和测试样本点间的距离来判定样本点是否是异常。

训练

假设输入样本空间$X\subseteq\mathbb{R}^d$,输出$\mathcal{F}\subseteq\mathbb{R}^p$,神经网络的特征映射函数为 $\phi(\cdot;W):\mathcal{X}\to\mathcal{F}$, 对应的参数为$\mathcal{W}=\{\overline{\boldsymbol{W}^1},\ldots,\boldsymbol{W^L}\}$,对于样本$x\in\mathcal{X}$的特征表示为$\phi(x;\mathcal{W})$, Deep SVDD 的目标是使输出特征空间中的样本点在最小的体积的超球面中，超球面可以使用球心 $c$ 和半径 $R$ 进行表示。对于给定的训练样本点集合$\mathcal{D}_n=\{\boldsymbol{x}_1,\ldots,\boldsymbol{x}_n\}$,定义 Deep SVDD 的 soft-boundary 的优化函数为 $$ \min\limits_{R,\mathcal{W}}\quad R^2+\frac{1}{\nu n}\sum\limits_{i=1}^n\max\left\{0,\left\|\phi\left(\boldsymbol{x}_i;\mathcal{W}\right)-\boldsymbol{c}\right\|^2-R^2\right\}+\frac{\lambda}{2}\sum\limits_{\ell=1}^L\left\|\boldsymbol{W}^\ell\right\|_F^2 $$

这种范式下训练数据中既可以存在正样本也可以存在负样本。第一项表示最小化超球面体积；第二项表示位于超球面外的惩罚项，其中超参数 $v$ 来平衡边界；第三项表示网络权重正则化防止过拟合。

这种范式下训练数据中既可以存在正样本也可以存在负样本，和传统 SVDD 相差不大。第一项表示最小化超球面体积；第二项表示位于超球面外的惩罚项，其中超参数 $v$ 来平衡边界；第三项表示网络权重正则化防止过拟合。

由于训练数据中大部分样本点都是正常的，因此论文对目标函数进行简化提出 One-Class Deep SVDD 范式

$$ \min_{\mathcal{W}}\frac{1}{n}\sum_{i=1}^{n}\left\|\phi\left(\boldsymbol{x}_{i};\mathcal{W}\right)-\boldsymbol{c}\right\|^{2}+\frac{\lambda}{2}\sum_{\ell=1}^{L}\left\|\boldsymbol{W}^{\ell}\right\|_{F}^{2} $$

One-Class Deep SVDD直接利用SGD进行优化。
soft-boundary范式在进行优化时需要借用minimization/block coordinate descent的方法，即固定R，网络训练k轮优化参数W；每经过k轮，利用最新更新的W来优化参数 R，R 可以通过 line search 进行搜索。

推断

对于测试样本点 $x\in X$, 可以定义异常分数为输出空间中样本点到超球面球心的距离

$$ s(\boldsymbol{x})=\left\|\phi\left(\boldsymbol{x};\mathcal{W}^*\right)-\boldsymbol{c}\right\|^2 $$

$\mathcal{W}^*$ 表示训练后模型权重，将该结果与 $R$ 进行比较即可得出结果。

优化

权重是全０的话，网络产生一个常数函数映射到超球中心，导致超球崩溃，因为超球半径为０，因此网络权重不可以为 0。
网络中的隐藏层有偏移项 bias，将会学习到一个常数函数映射导致超球崩溃
$$ \boldsymbol{z}^\ell(\boldsymbol{x})=\sigma^\ell\left(\boldsymbol{W}^\ell\cdot\boldsymbol{z}^{\ell-1}(\boldsymbol{x})+\boldsymbol{b}^\ell\right), $$
具有有界激活函数的网络单元，会在后续层中模拟偏移项，因此在 Deep SVDD 中应首选无界激活函数如 ReLU，以避免由于“学习”偏移项导致的超球崩溃。