飞行器坐标系及坐标变换知识总结

本文最后更新于：2024年8月13日下午

飞行器姿态变换过程中经常用到各种坐标系和坐标转换，本文记录相关内容。

视频教程

坐标系介绍

物体的位置、角度、速度都是相对观测坐标系(地面坐标系、北天东坐标系)，角速度等相对自身坐标系。

大地坐标系

即 WGS84(WorldGeodeticCoordinateSystem1984) 坐标系

这是为GPS全球定位系统建立的坐标系统。WGS-84坐标系的原点在地球质心，Z轴指向BIH1984.0定义的协定地球极（CTP）方向，X轴指向BIH1984.0的零度子午面和CTP赤道的交点，Y轴和Z、X轴构成右手坐标系。其参数为经度、纬度、海拔高度。

地球中心坐标系

ECEF（Earth-Centered, Earth-Fixed）

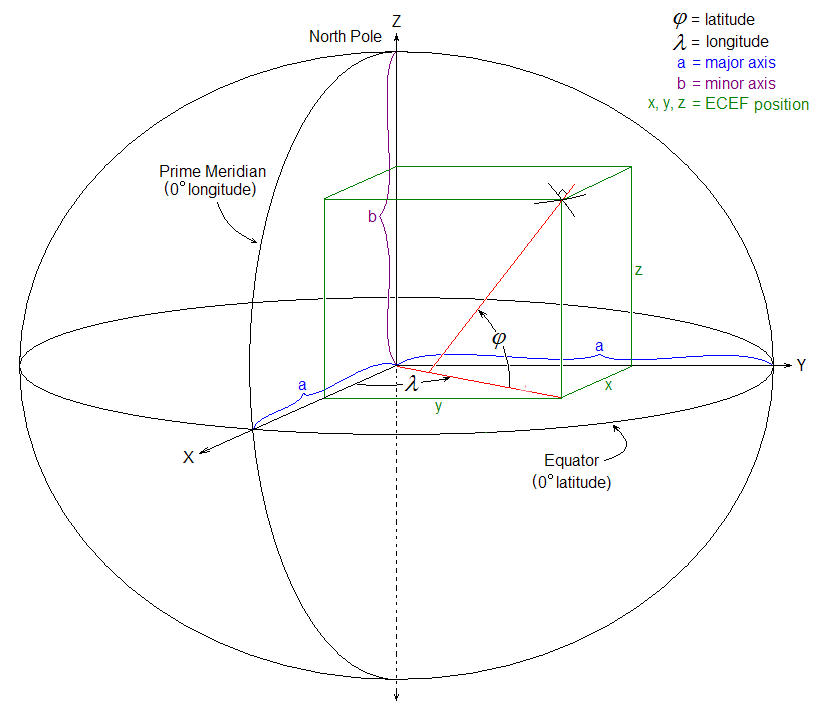
ECEF坐标系与地球固联，且随着地球转动。图中O即为坐标原点，位置在地球质心。X轴通过格林尼治线和赤道线的交点，正方向为原点指向交点方向。Z轴通过原点指向北极。Y轴与X、Z轴构成右手坐标系。

下图中可以直观的看出ECEF和WGS84坐标系的区别：

局部切线平面

从定义来分类，局部切线平面可分为基于垂直和水平尺寸定义的平面，其表现在纵坐标为上还是下。纵坐标为上时，称为ENU（东、北、天）坐标系，主要用于地理方面；纵坐标为下时，称为NED（北、东、地）坐标系，特别用于航空航天。

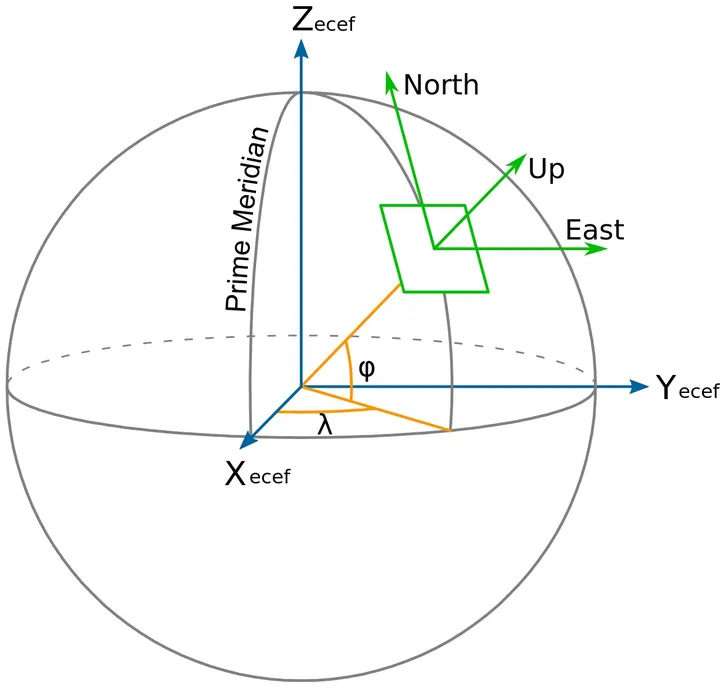
上图为ENU坐标系，该坐标系即为控制装置所在位置的“平面坐标系”，又称为 地理坐标系。

目标坐标系

雷达的重要作用是观测目标，通常目标运动(自身刚体运动)特性在目标坐标系中描述。坐标原点在目标质心处。如下图所示。

地面坐标系

地面坐标系的原点一般为雷达所在位置或火力单元位置，如下图所示。

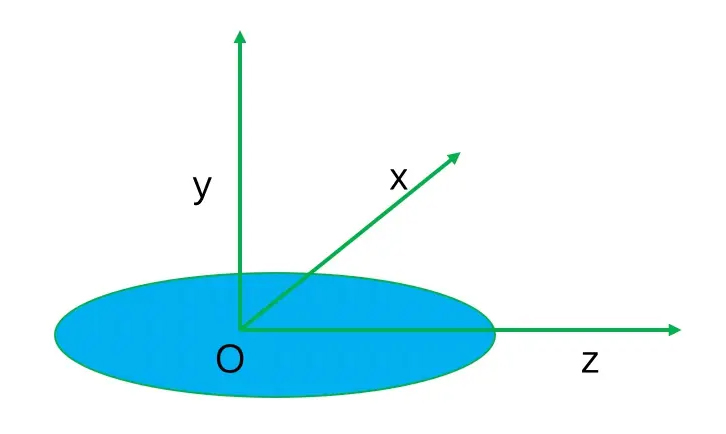
北天东坐标系

即北、天和东分别为坐标轴的X、Y和Z轴，如下图所示。

平台坐标系

若雷达在运动平台上，如飞机、导弹等，平台运动一般在平台坐标系中描述。飞机的姿态角(偏航、俯仰和横滚)是在大地坐标系下定义和描述的。

天线坐标系

天线坐标系原点在平台上的某个位置，通过平台坐标系方位和俯仰(角)旋转得到。若为正前视，则与平台坐标系一致。

坐标转换

目标坐标系到地面坐标系

若目标的姿态角分别为𝜙,𝜃和𝛾分别对应偏航、俯仰和横滚产生的角度，$𝑃_0$为目标在地面坐标系的坐标，则有目标点在地面坐标系中的坐标为
$$
P^{\prime}=R_{x}(\gamma) R_{y}(\theta) R_{z}(\phi) \times P+P_{0}
$$
其中：

$$ \begin{array}{l}R_{t g}=R_{x}(\gamma) R_{y}(\theta) R_{z}(\phi) \\ =\left[\begin{array}{ccc}1 & 0 & 0 \\ 0 & \cos \gamma & \sin \gamma \\ 0 & -\sin \gamma & \cos \gamma\end{array}\right]\left[\begin{array}{ccc}\cos \theta & 0 & -\sin \theta \\ 0 & 1 & 0 \\ \sin \theta & 0 & \cos \theta\end{array}\right]\left[\begin{array}{ccc}\cos \phi & \sin \phi & 0 \\ -\sin \phi & \cos \phi & 0 \\ 0 & 0 & 1\end{array}\right]\end{array} $$

地面坐标系到北天东坐标系

由定义可知，此转换相当于沿Y轴旋转90度，再沿Z轴旋转90度，可以得到如下变换：

$$ P^{\prime}=R_{z}\left(90^{\circ}\right) R_{y}\left(90^{\circ}\right) \times P $$

其中:

$$ R_{g e}=R_{z}\left(90^{\circ}\right) R_{y}\left(90^{\circ}\right)=\left[\begin{array}{ccc} 0 & 1 & 0 \\ -1 & 0 & 0 \\ 0 & 0 & 1 \end{array}\right]\left[\begin{array}{ccc} 0 & 0 & -1 \\ 0 & 1 & 0 \\ 1 & 0 & 0 \end{array}\right]=\left[\begin{array}{lll} 0 & 1 & 0 \\ 0 & 0 & 1 \\ 1 & 0 & 0 \end{array}\right] $$

北天东坐标系到平台坐标系

根据平台的三个姿态角偏航角𝜓、俯仰角𝜃和横滚角𝛾，平台位置为$𝑃_1$，则有:
$$
P^{\prime}=R_{x}(\gamma) R_{z}(\theta) R_{y}(\psi) \times P-P_{1}
$$
其中：

$$ \begin{array}{l}R_{e b}=R_{x}(\gamma) R_{z}(\theta) R_{y}(\psi) \\ \quad=\left[\begin{array}{ccc}1 & 0 & 0 \\ 0 & \cos \gamma & \sin \gamma \\ 0 & -\sin \gamma & \cos \gamma\end{array}\right]\left[\begin{array}{ccc}\cos \theta & \sin \theta & 0 \\ -\sin \theta & \cos \theta & 0 \\ 0 & 0 & 1\end{array}\right]\left[\begin{array}{ccc}\cos \psi & 0 & -\sin \psi \\ 0 & 1 & 0 \\ \sin \psi & 0 & \cos \psi\end{array}\right] \\ =\left[\begin{array}{ccc}\cos \theta & \sin \theta & 0 \\ -\cos \gamma \sin \theta & \cos \gamma \cos \theta & \sin \gamma \\ \sin \gamma \sin \theta & -\sin \gamma \cos \theta & \cos \gamma\end{array}\right]\left[\begin{array}{ccc}\cos \psi & 0 & -\sin \psi \\ 0 & 1 & 0 \\ \sin \psi & 0 & \cos \psi\end{array}\right] \\ =\left[\begin{array}{ccc}\cos \theta \cos \psi & \sin \theta & -\cos \theta \sin \psi \\ -\cos \gamma \sin \theta \cos \psi+\sin \gamma \sin \psi & \cos \gamma \cos \theta & \cos \gamma \sin \theta \sin \psi+\sin \gamma \cos \psi \\ \sin \gamma \sin \theta \cos \psi+\cos \gamma \sin \psi & -\sin \gamma \cos \theta & -\sin \gamma \sin \theta \sin \psi+\cos \gamma \cos \psi\end{array}\right]\end{array} $$

平台坐标系到天线坐标系

设天线与平台坐标系下的俯仰角和方位角分别为𝛼和𝛽，天线中心坐标为$𝑃_2$，则有如下变换
$$
P^{\prime}=R_{y}(\beta) R_{z}(\alpha) \times P-P_{2}
$$

其中:

$$ \begin{array}{l} R_{b a}=R_{y}(\beta) R_{z}(\alpha) \\ =\left[\begin{array}{ccc} \cos \beta & 0 & -\sin \beta \\ 0 & 1 & 0 \\ \sin \beta & 0 & \cos \beta \end{array}\right]\left[\begin{array}{ccc} \cos \alpha & \sin \alpha & 0 \\ -\sin \alpha & \cos \alpha & 0 \\ 0 & 0 & 1 \end{array}\right] \\ =\left[\begin{array}{ccc} \cos \beta \cos \alpha & \cos \beta \sin \alpha & -\sin \beta \\ -\sin \alpha & \cos \alpha & 0 \\ \sin \beta \cos \alpha & \sin \beta \sin \alpha & \cos \beta \end{array}\right] \end{array} $$