相机成像的几何原理

本文最后更新于：2023年12月5日下午

真实物体通过相机转换为图像，可以通过一个数学模型将真实物体的三维坐标与图像中的二维坐标一一对应，本文从几何角度解释图像的形成。

简介

为了轻松理解问题，我们假设您在一个房间内部署了一个摄像头。给定这个房间中的 3D 点 $P$，我们想在相机拍摄的图像中找到该 3D 点的像素坐标 $(u,v)$。

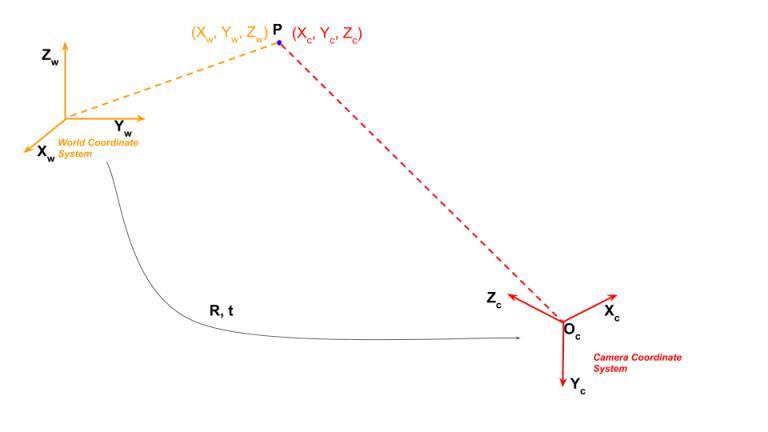
从三维坐标（世界坐标系）到二维坐标（图像坐标系）又可以分为三个步骤：

从世界坐标转换到相机坐标；
从相机坐标转换到图像坐标；
从图像坐标转换到像素坐标。

世界坐标到相机坐标系

世界坐标系

要定义房间中点的位置，我们首先需要为此房间定义一个坐标系。它需要两件事：

原点：我们可以任意固定房间的一角作为原点 $(0,0,0)$。
$X,Y,Z$轴：我们还可以沿着地板的两个维度定义房间的 $X$ 和 $Y$ 轴，并沿着垂直墙定义 $Z$ 轴。

使用以上坐标系定义，我们可以找到房间中任何点的3D坐标，此坐标系称为 世界坐标系(World Coordinate System)，也就是图中的黄色坐标系。

在世界坐标系中，我们可以定义房间的点 $P$ 坐标为 $(X_w,Y_w,Z_w)$。

相机坐标系

现在，在这个房间里放一个相机。使用此摄像机将捕获房间的图像，因此，我们对连接到此摄像机的3D坐标系感兴趣，并且需要找到 3D 世界坐标与 3D 摄像机坐标之间的关系。

将相机放在房间的任意位置，拍摄任意方向，此时都可以以相机位置为原点，以相机的水平、镜头正对的方向、竖直方向作为$(X_c,Y_c,Z_c)$ 轴建立坐标系，该坐标系定义为 相机坐标系（ Camera Coordinate System ）。

外部参数

相机坐标系可以通过平移和旋转达到与世界坐标系重合的效果，因此可以说世界坐标系和摄影机坐标系通过旋转和平移关联，这其中有六个参数（3个用于旋转，3个用于平移）称为相机的外部参数。

将旋转和平移都用矩阵乘法表示，旋转矩阵为 $R$ (9个参数，自由度为3)，平移向量 $t$，那么坐标值可以通过以下公式关联：

$$ \left[\begin{array}{c}X_{c} \\ Y_{c} \\ Z_{c}\end{array}\right]=\mathbf{R}\left[\begin{array}{c}X_{w} \\ Y_{w} \\ Z_{w}\end{array}\right]+\mathbf{t} $$

有时，上面的表达式以更紧凑的形式编写。将 $3×1$ 平移向量作为列附加在 $3×3$ 旋转矩阵的末尾，以获得称为外部矩阵（相机外参）的 $3×4$ 矩阵。

$$ \left[\begin{array}{c}X_{c} \\ Y_{c} \\ Z_{c}\end{array}\right]=[\mathbf{R} \mid \mathbf{t}]\left[\begin{array}{c}X_{w} \\ Y_{w} \\ Z_{w} \\ 1\end{array}\right] $$

外参矩阵 $P$ 定义为：
$$
\mathbf{P}=[\mathbf{R} \mid \mathbf{t}]
$$

从相机坐标转换到图像坐标

图像坐标系

上图显示了点 P 在小孔成像相机图像平面上的投影，图像平面放置在距光学中心一定距离 $f$ （焦距）的位置。感光原件会在焦距位置设置一个平面，这里的坐标系称作图像坐标系（Image Coordinate System ）。

相机坐标转换到图像坐标

P 在投影平面上的点 $(x,y)$ 可以通过如下计算获取：

$$ \begin{aligned} y_{p} & =f \times \frac{Y c}{Z c} \\ x_{p} & =f \times \frac{X c}{Z c}\end{aligned} $$

矩阵 $K$ 称为内部矩阵，包含相机的内部参数：

$$ \mathbf{K}=\left[\begin{array}{lll}f & 0 & 0 \\ 0 & f & 0 \\ 0 & 0 & 1\end{array}\right] $$

相机坐标到图像坐标的转换过程为：

$$ \left[\begin{array}{c}x_{p} \\ y_{p} \\ 1\end{array}\right]=\frac{1}{Z_{ c}}\left[\begin{array}{ccc}f x & 0 & 0 \\ 0 & f y & 0 \\ 0 & 0 & 1\end{array}\right]\left[\begin{array}{l}X_{ c} \\ Y_{ c} \\ Z_{ c}\end{array}\right] $$

从图像坐标转换到像素坐标

图像坐标系平面可以认为是理想的成像面，像素坐标系则是相机传感器平面，理想情况下图像坐标平面和像素坐标平面在同一平面，则从图像坐标转换到像素坐标有两个步骤：

缩放，在前面的坐标系中，坐标系单位是统一的实际距离单位，但是像素坐标系的单位不一样，因此要缩放，换算到像素坐标系；
平移，从图像坐标系原点到像素坐标系原点。

变换为：

$$ \left[\begin{array}{c}u_{p} \\ v_{p} \\ 1\end{array}\right]=\left[\begin{array}{ccc}s x & 0 & c x \\ 0 & s y & c y \\ 0 & 0 & 1\end{array}\right]\left[\begin{array}{c}x_{p} \\ y_{p} \\ 1\end{array}\right] $$

其中 $sx$ 和 $sy$ 为单位长度的像素数。

同时，在实际中可能由于相机传感器的问题导致图像轴不垂直的情况，如下图：

可以认为在 $y$ 方向坐标不变，$x$ 方向坐标存在偏移，则有：

$$ \left[\begin{array}{c}u_{p} \\ v_{p} \\ 1\end{array}\right]=\left[\begin{array}{ccc}s x & c & c x \\ 0 & s y & c y \\ 0 & 0 & 1\end{array}\right]\left[\begin{array}{c}x_{p} \\ y_{p} \\ 1\end{array}\right] $$

其中 $c$ 为偏移系数。

坐标转换汇总

由上文推导总结得到由世界坐标到像素坐标转换关系：

$$ \left[\begin{array}{c}u_{p} \\ v_{p} \\ 1\end{array}\right]=\left[\begin{array}{ccc}s x & c & c x \\ 0 & s y & c y \\ 0 & 0 & 1\end{array}\right] \frac{1}{Z_{p c}}\left[\begin{array}{ccc}f x & 0 & 0 \\ 0 & f y & 0 \\ 0 & 0 & 1\end{array}\right][R \mid t]\left[\begin{array}{c}X _w \\ Y_ w \\ Z _w \\ 1\end{array}\right] $$

即：

$$ s\left[\begin{array}{c}u_{p} \\ v_{p} \\ 1\end{array}\right]=\left[\begin{array}{ccc}f_{x} s_{x} & c & c x \\ 0 & f_{y} s_{y} & c y \\ 0 & 0 & 1\end{array}\right][R \mid t]\left[\begin{array}{c}X_ w \\ Y _ w \\ Z _ w \\ 1\end{array}\right] $$

得到：
$$
s \tilde{m}=\mathbf{A}[\mathbf{R} \mid \mathbf{t}] \tilde{\mathbf{M}}
$$
其中：

$ s=1 / Z p c $ 为尺度参数
$ \mathbf{A} $ 是相机内参 $ , \mathbf{R}, \mathbf{t} $ 是相机外参
$$ A=\left[\begin{array}{ccc}f_{x} s_{x} & c & c x \\ 0 & f_{y} s_{y} & c y \\ 0 & 0 & 1\end{array}\right] $$
$ \tilde{m} $ 为图像的齐次坐标 $ [u, v, 1]^{T} $
$ \tilde{M} $ 为模型点的齐次坐标 $ [X _w, Y _ w, Z _ w, 1]^{T} $