道格拉斯普克 (Douglas-Peuker) 算法

本文最后更新于：2024年6月26日下午

在描述路径时经常会使用折线，而折线有时需要做近似的简化，Douglas-Peuker 算法是一种简单快速的路径近似算法，本文介绍原理和 python 实现。

简介

道格拉斯-普克算法（Douglas–Peucker algorithm），亦称为拉默-道格拉斯-普克算法（Ramer–Douglas–Peucker algorithm），这个算法最初由拉默（Urs Ramer）于1972年提出，1973年道格拉斯（David Douglas）和普克（Thomas Peucker）二人又独立于拉默提出了该算法。

在计算机当中，曲线可以用足够多的点来描述，那么如何用尽可能少的点来描述这条曲线呢，这就是该算法要实现的目标，同时因为用来描述曲线的点变少了，也可以认为其对数据进行了压缩，减少了数据量。

算法

起始曲线是一组有序的点或线，距离维度 ε > 0。

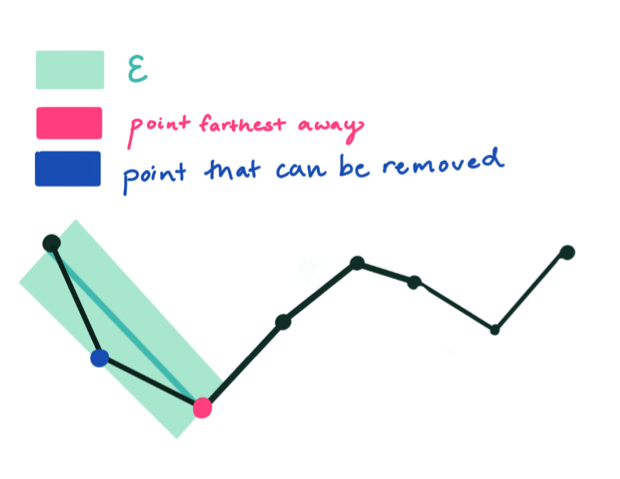
该算法递归划分线。最初，它被赋予了第一点和最后一点之间的所有点。它自动标记要保留的第一点和最后一点。然后它找到离以第一点和最后一点为终点的线段最远的点；这个点显然是曲线上离终点之间的近似线段最远的点。如果这个点离线段的距离比 ε 更近，那么在简化曲线不比 ε 差的情况下，可以舍弃任何当前没有标记保留的点。

如果离线段最远的点大于近似值 ε，那么该点必须保留。该算法以第一点和最远点递归调用自身，然后以最远点和最后一点调用自身，其中包括最远点被标记为保留。

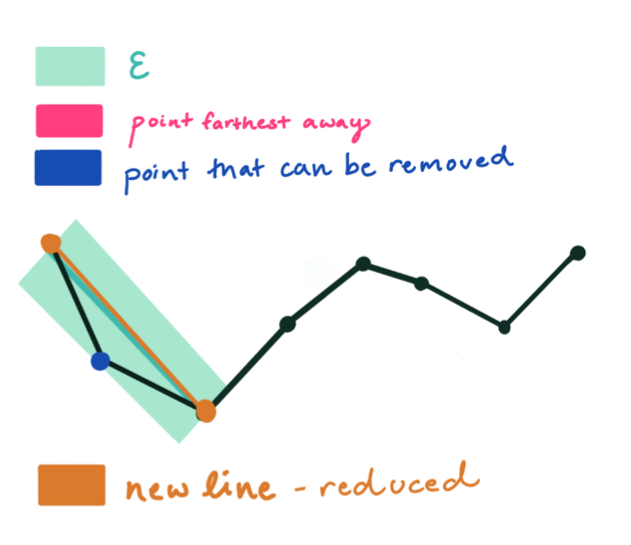
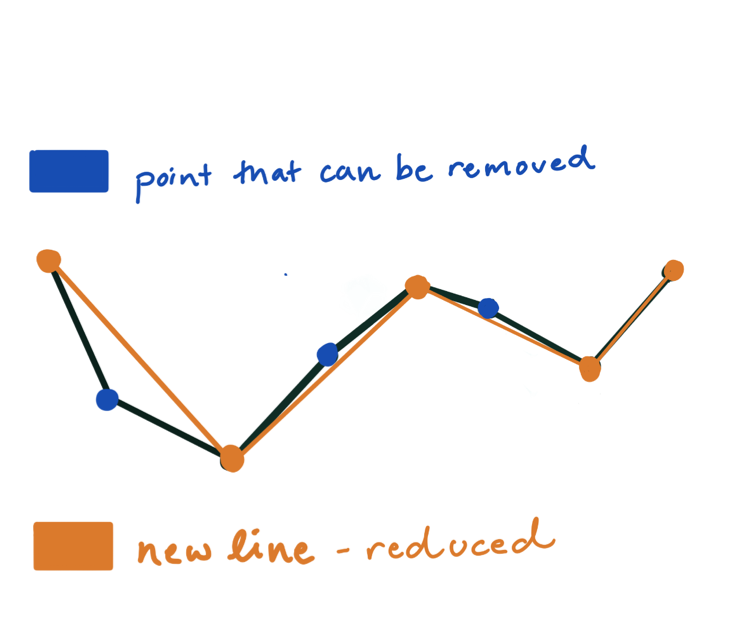
当递归完成后，可以生成一条新的输出曲线，该曲线由所有且仅由那些被标记为保留的点组成。

算法流程

首先明确程序的 输入是一系列的点构成的曲线，输出的是其中一部分点构成的曲线；
将曲线首尾AB两点连成一条直线（程序中应当是理论计算出）；
然后分别计算曲线上各点到这条直线的距离，并取出其中的最远距离与阈值进行比较（该阈值通常人为确定）；
若是大于阈值，则保留该最大距离对应的点C，此时可以生成两条直线AC、CB，重复步骤三；
若是小于阈值，则算法结束。

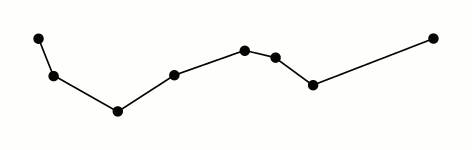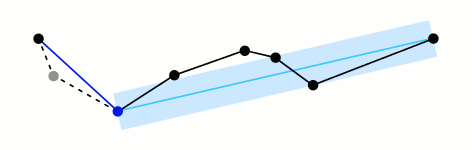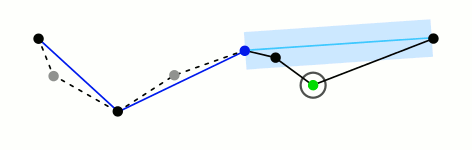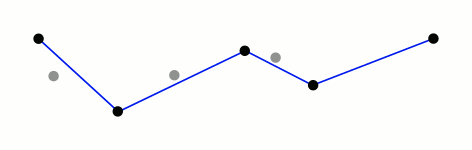
图解流程

绿色的宽度就代表阈值
红色代表每次算法中最远的点
蓝色表示可以被移除的点
橙色表示最后生成的曲线

伪代码

function DouglasPeucker(PointList[], epsilon)
    // Find the point with the maximum distance
    dmax = 0
    index = 0
    end = length(PointList)
    for i = 2 to (end - 1) {
        d = perpendicularDistance(PointList[i], Line(PointList[1], PointList[end]))
        if (d > dmax) {
            index = i
            dmax = d
        }
    }
    
    ResultList[] = empty;
    
    // If max distance is greater than epsilon, recursively simplify
    if (dmax > epsilon) {
        // Recursive call
        recResults1[] = DouglasPeucker(PointList[1...index], epsilon)
        recResults2[] = DouglasPeucker(PointList[index...end], epsilon)

        // Build the result list
        ResultList[] = {recResults1[1...length(recResults1) - 1], recResults2[1...length(recResults2)]}
    } else {
        ResultList[] = {PointList[1], PointList[end]}
    }
    // Return the result
    return ResultList[]
end

复杂度

该算法在由 ${\displaystyle n-1}$ 段和 ${\displaystyle n}$ 个顶点组成的折线上运行时的时间由递归 ${\displaystyle T(n)=T(i+1)+T(n-i)+O(n)}$ 给出，其中 ${\displaystyle i\in {1,\ldots ,n-2}} $ 是伪代码中的索引值。在最坏的情况下，每次递归调用时，${\displaystyle i=1}$ 或 ${\displaystyle i=n-2}$，该算法的运行时间为 ${\displaystyle \Theta (n^{2})}$。在最好的情况下，在每次递归调用时，${\displaystyle i=\lfloor n/2\rfloor }$ 或 ${\displaystyle i=\lceil n/2\rceil }$，在这种情况下，运行时间具有 ${\displaystyle O(n\log n)}$ 的众所周知的解（通过分治法的主定理）。

OpenCV 实现

在OpenCV Python中，cv.approxPolyDP是一个用于多边形逼近的函数。它使用Douglas-Peucker算法来减少多边形的点数。

该函数需要两个参数：输入多边形和一个表示逼近精度的参数。输入多边形是一个由点组成的数组，而逼近精度是一个用于控制轮廓近似的精度参数。

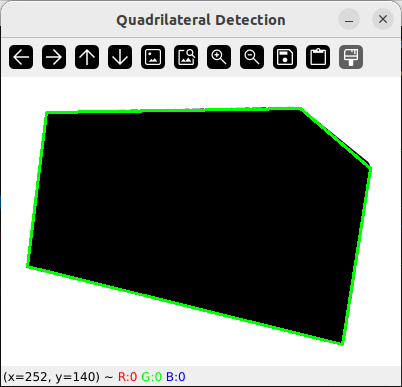
测试图像：

import cv2


# 读取图像
image = cv2.imread('test.png')

# 灰度化处理
gray = (cv2.cvtColor(image, cv2.COLOR_BGR2GRAY) < 1).astype('uint8')

# 轮廓检测
contours, _ = cv2.findContours(gray, cv2.RETR_EXTERNAL, cv2.CHAIN_APPROX_NONE)

for contour in contours:
    epsilon = 0.01 * cv2.arcLength(contour, True)
    approx = cv2.approxPolyDP(contour, epsilon, True)

    cv2.drawContours(image, [approx], 0, (0, 255, 0), 2)

# 绘制四边形
cv2.imshow('Quadrilateral Detection', image)
cv2.waitKey(0)
cv2.destroyAllWindows()