A-Star 算法详解

A*（A-Star)算法是一种静态路网中求解最短路径的搜索方法, 本文记录相关内容。

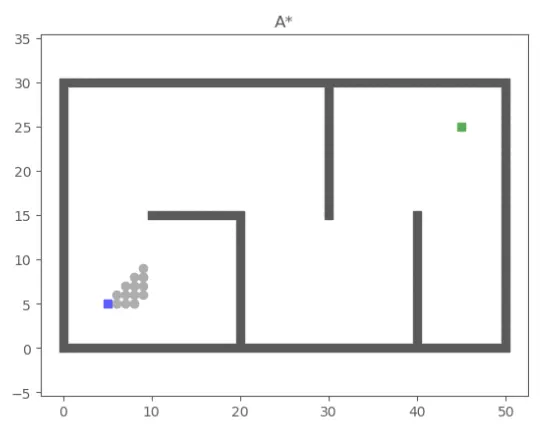
简介

A*算法是一个“搜索算法”，目的是在一个图上“求解最短路径”，实质上是 Dijsktra 的升级版，加入了启发式搜索，从而减少搜索范围，提高效率。

核心思想

通过评估函数 **f(n) = g(n) + h(n)**指导 搜索方向，其中：

1. g(n)：从起点到当前节点n的实际路径代价。
2. h(n)（启发式函数）：当前节点到目标节点的估计代价，需满足可采纳性（即不高估实际代价，如曼哈顿距离用于四方向移动网格）。

注意: 如果启发式函数h(n)不满足可采纳性，A*可能无法找到最优解。另外，如果h(n)是一致的（也就是满足三角不等式），那么A*算法在扩展节点时一旦找到目标节点就可以立即停止，因为此时的路径已经是最优的了。否则可能需要继续检查以确保最优性。

算法流程

1. 初始化开放列表（优先队列）和封闭列表（记录已处理节点），将起点加入开放列表。
2. 循环直到找到目标或开放列表为空：
   • 取出开放列表中f(n) 最小的节点 n。
   • 若n是目标，回溯路径并结束。
   • 将n移入封闭列表，扩展其相邻节点。
   • 对每个相邻节点m：
     • 若m在封闭列表中，跳过。
     • 计算新g(m)，若更优或m未在开放列表中，更新g(m)、f(m)，并将m加入开放列表。

关键点

• 最优性保证：当**h(n)**可采纳时，A* 能找到最短路径。
• 效率：启发式函数质量决定搜索速度。若**h(n)**接近实际代价（如对角线距离允许八方向移动时），节点扩展更少。
• 对比：
  • Dijkstra：无启发式（h(n)=0），扩展更多节点。
  • 最佳优先搜索：仅用h(n)，不保证最优。

常用启发式函数

对于网格形式的图，有以下这些启发函数可以使用：

• 若图形中只允许朝上下左右四个方向移动，使用曼哈顿距离：
  $$
  d=|x_1-x_2|+|y_1-y_2|
  $$

• 若图形中允许朝八个方向移动，使用对角距离：
  $$
  d= max(|x_1-x_2|,|y_1-y_2|)
  $$

• 若图形中允许朝任何方向移动：使用欧几里得距离：
  $$
  d=\sqrt{(x_1-x_2)^2+(y_1-y_2)2}
  $$

参考资料

• https://blog.csdn.net/a_vegetable/article/details/115361888

文章链接：
https://www.zywvvd.com/notes/study/algorithm/graph/astar/astar/