拉格朗日对偶问题

在前文了解过拉格朗日乘数法后，进一步介绍拉格朗日对偶。

背景信息

在约束最优化问题中，常常利用拉格朗日对偶性（Lagrange duality）将原始问题转换为对偶问题，通过解对偶问题而得到原始问题的解。

• 拉格朗日对偶是在拉格朗日乘数法基础之上，通过变换原始问题的求解形式得到的相对于原始优化问题的另一个优化问题

原始优化问题

假设$f(x)$, $c_i(x)$, $h_j(x)$ 是定义在$\mathbf{R}^{n}$上的连续可微函数，考虑约束最优化问题：

$$ \begin{array}{c} \min _{x \in \mathbf{R}^{n}} f(x) \\ \text { s.t. } \quad h_{i}(x) \leq 0, i=1,2, \ldots, k \\ g_{j}(x)=0, j=1,2, \ldots, l \end{array}\tag{1} \label{eq1} $$

• 定义此问题为原始优化问题

广义拉格朗日函数

来源见 ：拉格朗日乘数法

$$
L(x, \alpha, \beta)=f(x)+\sum_{i=1}^{k} \alpha_{i} h_{i}(x)+\sum_{j=1}^{l} \beta_{j} g_{j}(x)\tag{2} \label{eq2}
$$

• 其中 $x=\left(x_1, x_2, \ldots, x_n\right)^{T} \in \mathbf{R}^{n} , \alpha_{i}, \beta_{j}$是拉格朗日乘子，且$\alpha_{i} \geq 0$
• 原始优化问题需要先确定选择哪个不等式约束（即定义哪个 $\alpha_i$ 不等于零），放弃哪个不等式约束（定义哪个 $\alpha_i$ 等于零）
• 那么由于原始问题的状态，$\alpha $ 非负，不等式约束非正，那么问题为了收敛需要最大化 $L$

$$ \max _{\alpha_{i} \geq 0} {L}(x, \alpha, \beta) \tag{3} \label{eq3} $$

• 即当所有约束都满足时，$\max_{\alpha_{i} \geq 0} L$ 为 $f(x)$，否则为 $ +\infty $
• 通过最大化 $L$ 确定 $\alpha$，之后仅剩下等式约束，$L$ 也变为了原始的 $f(x)$，之后才可以按照原始目标正常求解极值:

$$ \min_{x} \max _{\alpha_{i} \geq 0} {L}(x, \alpha, \beta) \tag{4} \label{eq4} $$

• 这即是原始问题的求解方式。

拉格朗日对偶的来源

考虑原始优化问题$\eqref{eq1}$

• 想要求得$f(x)$的最小值，也就是要求$f(x)$的最大下界
• 对于方程组：

$$
\begin{array}{l}
f(\mathbf{x})<v \\
h_{i}(\mathbf{x}) \leq 0, i=1,2, \ldots, k
\end{array} \tag{5} \label{eq5}
$$

• 若方程组$\eqref{eq5}$无解，则$v$是$f(x)$的一个下界，也就是说如果有渠道可以利用到方程组$\eqref{eq5}$无解，则可以利用其限制$f(x)$的下界
• 注意到若方程组$\eqref{eq5}$有解，可以推出对于任意$\lambda \ge 0$：

$$
f(\mathbf{x})+\sum_{i=1}^{k} \lambda_{i} h_{i}(\mathbf{x})<v \tag{6} \label{eq6}
$$

• 方程$\eqref{eq6}$有解
• 即命题：if 方程组$\eqref{eq5}$有解 then 方程$\eqref{eq6}$有解 成立
• 则其逆否命题 $if$ 方程$\eqref{eq6}$无解 $then$ 方程组$\eqref{eq5}$无解 成立
• 而 方程$\eqref{eq6}$无解 的充要（等价）条件是：

$$ \min _{ \mathbf{x} } f ( \mathbf {x} ) + \sum _ { i=1 } ^ {k} \lambda_{i} g_{i} ( \mathbf {x}) \geq v \tag{7} \label{eq7} $$

• 方程$\eqref{eq7}$的自变量为$\lambda_i$，我们的目标是要找到其上界$v_{max}$，因此有：

$$ v_{max}=\max _{\boldsymbol{\lambda} \geq \mathbf{0}} \min _{\mathbf{x}} f(\mathbf{x})+\sum_{i=1}^{k} \lambda_{i} g_{i}(\mathbf{x}) \tag{8} \label{eq8} $$

• 方程$\eqref{eq8}$即为拉格朗日对偶问题的核心，延续原始问题的标记，记为：

$$ \mathop {\max }\limits_{\alpha \cdot \beta ;{\alpha _i} \ge 0}D(\alpha ,\beta ) = \mathop {\max }\limits_{\alpha \cdot \beta ;{\alpha _i} \ge 0} \mathop {\min }\limits_x L(x,\alpha ,\beta )\tag{9} \label{eq9} $$

可以说对偶问题就是从另一个方向逼近$f(x)$最小值的问题

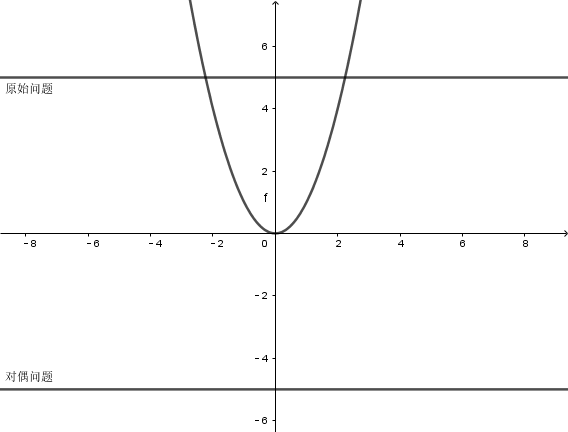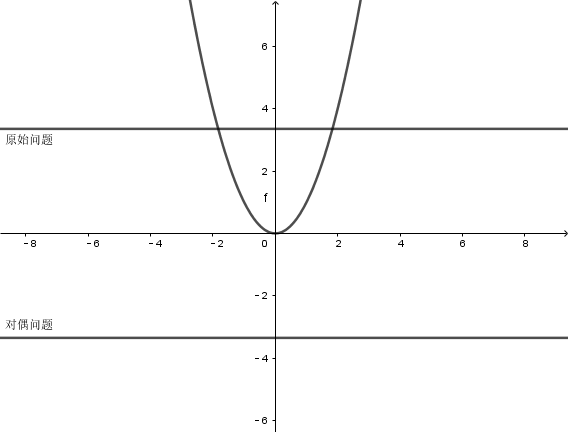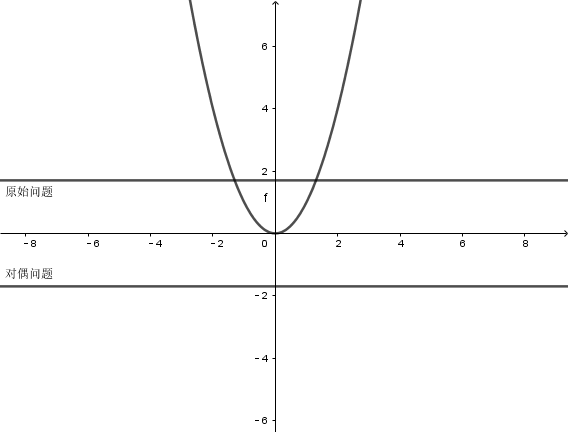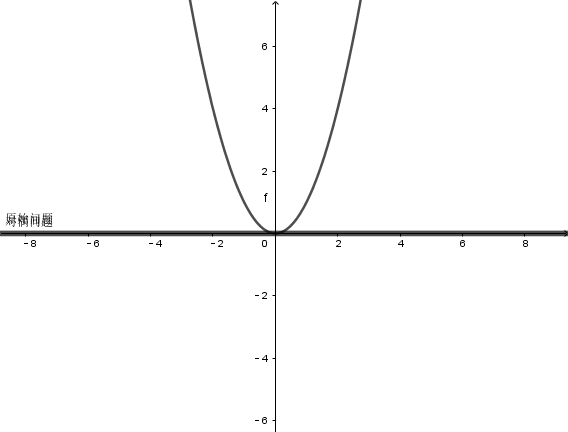
对偶问题的性质

之所以引入另一个优化问题是因为对偶问题之间有着良好的性质

• 对偶问题的对偶是原问题；
• 无论原始问题是否是凸的，对偶问题都是凸优化问题；
• 对偶问题可以给出原始问题一个下界；
• 当满足一定条件时，原始问题与对偶问题的解是完全等价的；

拉格朗日对偶问题的凹函数性质证明

按照定义

对偶问题有一个很好的性质是对偶函数为凹函数，证明如下

• 命题 拉格朗日对偶函数一定是凹函数，且其凹性与最优化函数和约束函数无关。
• 考虑对偶问题$\eqref{eq9}$，按照凹函数定义，往证：

$$
D(\theta {\alpha _1} + (1 - \theta ){\alpha _2},\theta {\beta _1} + (1 - \theta ){\beta _2}) \ge \theta D({\alpha _1},{\beta _1}) + (1 - \theta )D({\alpha _2},{\beta _2}) \tag{10} \label{eq10}
$$

• 有：

$$ \begin{array}{l} &D(\theta {\alpha _1} + (1 - \theta ){\alpha _2},\theta {\beta _1} + (1 - \theta ){\beta _2}) \\ &= \mathop {\min }\limits_x L(x,\theta {\alpha _1} + (1 - \theta ){\alpha _2},\theta {\beta _1} + (1 - \theta ){\beta _2})\\ &= \mathop {\min }\limits_x (f(x) + \sum\limits_{i = 1}^k {(\theta {\alpha _{1,i}} + (1 - \theta ){\alpha _{2,i}})} {h_i}(x) + \sum\limits_{j = 1}^l {(\theta {\beta _{1,j}} + (1 - \theta ){\beta _{2,j}})} {g_j}(x)\\ &= \mathop {\min }\limits_x (\theta (f(x) + \sum\limits_{i = 1}^k {{\alpha _{1,i}}} {h_i}(x) + \sum\limits_{j = 1}^l {{\beta _{1,j}}} {g_j}(x)) + (1 - \theta )(f(x) + \sum\limits_{i = 1}^k {{\alpha _{2,i}}} {h_i}(x) + \sum\limits_{j = 1}^l {{\beta _{2,j}}} {g_j}(x)))\\ &\ge \theta \mathop {\min }\limits_x (f(x) + \sum\limits_{i = 1}^k {{\alpha _{1,i}}} {h_i}(x) + \sum\limits_{j = 1}^l {{\beta _{1,j}}} {g_j}(x)) + (1 - \theta )\mathop {\min }\limits_x (f(x) + \sum\limits_{i = 1}^k {{\alpha _{2,i}}} {h_i}(x) + \sum\limits_{j = 1}^l {{\beta _{2,j}}} {g_j}(x))\\ &= \theta D({\alpha _1},{\beta _1}) + (1 - \theta )D({\alpha _2},{\beta _2}) \end{array} \tag{11} \label{eq11} $$

• 其中$\eqref{eq11}$的不等式来源于：

  • 对于实数集合$\bf{a},\bf{b}$：
  $$ \begin{array}{l} a=\left\{a_{1}, a_{2}, \cdots, a_{n}\right\} \\ b=\left\{b_{1}, b_{2}, \cdots, b_{n}\right\} \end{array} \tag{12} $$
  • 对于任意$i$，有：
  $$ \mathop {\min }\limits_i \left\{ {{a_i} + {b_i}} \right\} \ge \min \{ {\bf{a}}\} + \min \{ {\bf{b}}\} ,\quad i \in {N^ + } \tag{13} $$

• 原命题得证。

仿射函数

另一种思路是讨论$\eqref{eq2}$的后两项内容

• 因为对偶问题中$x$视作常数，$\alpha,\beta$为自变量，可以视作：

$$ \begin{array}{l} D(\alpha ,\beta {\rm{|x}}) &= f(x) + \sum\limits_{i = 1}^k {{\alpha _i}} {h_i}(x) + \sum\limits_{j = 1}^l {{\beta _j}} {g_j}(x)\\ &= A + \sum\limits_{i = 1}^k {{\alpha _i}} {B_i} + \sum\limits_{j = 1}^l {{\beta _j}} {C_j} \end{array} \tag{14} $$

• 因此$D(\alpha, \beta)$是调整常数$A,B,C$的仿射函数，仿射函数既凸且凹，因此拉格朗日对偶问题具有凹函数性质

拉格朗日对偶

原始问题

• 考虑$x$的函数：

$$ P(x)=\max _{\alpha, \beta ; \alpha_{i} \geq 0} L(x, \alpha, \beta) \tag{15} $$

这里，$P$表示原始问题。将上式看做$x$ 的函数。

等式右边可以看做固定$x$ 的情况下，求关于$\alpha, \beta$的函数 $L $的最大值的问题。

• 可以推出：

$$ P(x)=\left\{\begin{array}{l} f(x), x \text { 满足原始问题约束 } \\ +\infty, \text { otherwise } \end{array}\right. \tag{16} $$

• 考虑极小化问题：

$$
\min _{x} P(x)=\min _{x} \max _{\alpha, \beta ; \alpha \geq 0} L(x, \alpha, \beta) \tag{17} \label{eq17}
$$

• 式$\eqref{eq17}$与$\eqref{eq9}$等价，因为固定$x$时剩余两项在约束范围内最大值为 0，相当于在约束范围内求解$f(x)$的最小值。
• 定义原始问题的值为：

$$
p^{*}=\min _{x} P(x) \tag{18}
$$

对偶问题

• 延续上文的对偶问题$\eqref{eq9}$
• 可以看到事实上对偶问题与原问题为极大极小的求解顺序问题
• 定义对偶问题的值：

$$ d^{*}=\max _{\alpha, \beta ; \alpha_{i} \geq 0} D(\alpha, \beta) \tag{19} $$

原始问题与对偶问题的关系

• 对偶问题的解不大于原始问题的解：
• 证明：

$$ \begin{array}{c}\\ D(a, \beta)=\min _{x} L(x, a, \beta) \leqslant L(x, a, \beta) \leqslant \max _{\sigma, \beta: a_{i} \geqslant 0} L(x, a, \beta)=P(x)\\ D(\mathrm{a}, \beta) \leqslant P(x)\\ \mathrm{d}^{*}=\max _{\mathrm{a}, \mathrm{B}: \mathrm{a}_{i} \geqslant 0} \min _{\mathrm{x}} L(x, \mathrm{a}, \beta) \leqslant \min _{\mathrm{x}} \max _{\mathrm{a}, \mathrm{\beta}: \mathrm{a}_{i} \geqslant 0} L(x, \mathrm{a}, \beta)=\mathrm{p}^{*}\\ d ^ { * } \le p ^ { * } \end{array}\tag{20} $$

• 该性质为弱对偶性（weak duality），该性质在任何情况下都成立
• 也因为弱对偶的存在，使得 对偶问题可以给出原始问题的下界
• 与弱对偶性相对应的是强对偶性（strong duality），即：

$$
d^{* } = p^{* } \tag{21}
$$

• 若强对偶性成立，即原始问题与对偶问题的最优值相等，则可以通过求解对偶问题来得到原始问题的解

强对偶成立条件

强对偶的性质太过于美妙，如果我们的问题满足强对偶条件，直接求对偶问题就好了

这里列出两个常见的条件

Convex + Slater

• 原问题是凸优化
  • $f(x)$和$h(x)$是凸函数
  • $g(x)$是放射函数
• 存在$x$使得不等式约束严格成立（严格成立不等号）

KKT 条件

原问题是否为凸函数的两种情况下，KKT的用法不同

原问题非凸

当原问题并非凸优化(或者不清楚、不关心是不是凸优化)时，KKT 条件是一种用来描述强对偶情况下最优解性质的条件
换而言之，若强对偶性质成立，那么满足最优解的点一定满足 KKT 条件；KKT 条件是强对偶一个必要条件，但无法作为充分条件来使用

原问题为凸函数

当原问题为凸优化时，KKT 条件在非凸的基础上有多了找到最优点的功能
在这种情况下，那么满足 KKT 条件的点一定是原问题和对偶问题的最优解；KKT 条件成了强对偶和最优解的充要条件

参考资料

• https://blog.csdn.net/qq_32742009/article/details/81413068
• https://blog.csdn.net/u014540876/article/details/79153913
• https://zhuanlan.zhihu.com/p/45431511
• https://www.zhihu.com/question/58584814
• https://blog.csdn.net/frostime/article/details/90291392

文章链接：
https://www.zywvvd.com/notes/study/machine-learning/lagrangian-duality/lagrangian-duality/