本文最后更新于：2024年8月30日 下午

Voronoi Diagram 是一种常出现在大自然之中的图案，也被广泛应用在我们的生活中，本文记录相关内容。

简介

荷兰气候学家A·H·Thiessen提出了一种根据离散分布的气象站的降雨量来计算平均降雨量的方法，即将所有相邻气象站连成三角形，作这些三角形各边的垂直平分线，于是每个气象站周围的若干垂直平分线便围成一个多边形。用这个多边形内所包含的一个唯一气象站的降雨强度来表示这个多边形区域内的降雨强度，并称这个多边形为泰森多边形。泰森多边形每个顶点是每个三角形的外接圆圆心，泰森多边形也称为Voronoi图。

想像在一个平面上，分布着N 个点，则Voronoi diagram 即是将此平面切分成各自只包含一个点的N个多边形（cell），使多边形内的每个位置到该点的距离相较于到其他点的距离为最近。

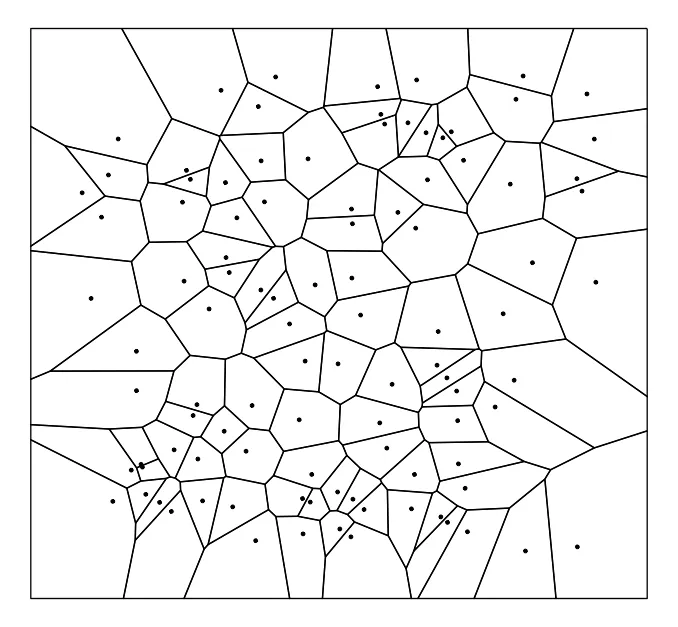
这样说明有点过于抽象，为了更容易帮助理解，在下图中，我绘制了一张带有 20 个点的Voronoi diagram。以蓝色的多边形为例，原先多边形中的黑点为A，在此多边形内任取一点X，则X 到画面上任意黑点的距离之中，X 点和A 点的距离会是最近的。

那么 Voronoi diagram 到底是如何画出来的呢？

答案意外的简单：Voronoi Diagram 为两两邻近点之间的中垂线相连而成的图案。因此图形中隐含着「邻近」的信息。

特点

Voronoi 图的特性是：

1，每个Voronoi 多边形内仅含有一个离散点数据。

2，Voronoi 多边形内的点到相应离散点的距离最近。

3，位于Voronoi多边形边上的点到其两边的离散点的距离相等。

泰森多边形可用于定性分析、统计分析、邻近分析等。例如，可以用离散点的性质来描述泰森多边形区域的性质；可用离散点的数据来计算泰森多边形区域的数据；判断一个离散点与其它哪些离散点相邻时，可根据泰森多边形直接得出，且若泰森多边形是n边形，则就与n个离散点相邻；当某一数据点落入某一泰森多边形中时，它与相应的离散点最邻近，无需计算距离。

建立步骤

建立泰森多边形算法的关键是对离散数据点合理地连成三角网，即构建Delaunay三角网。建立泰森多边形的步骤为：

1、离散点自动构建三角网，即构建Delaunay三角网。对离散点和形成的三角形编号，记录每个三角形是由哪三个离散点构成的。

2、找出与每个离散点相邻的所有三角形的编号，并记录下来。这只要在已构建的三角网中找出具有一个相同顶点的所有三角形即可。

3、对与每个离散点相邻的三角形按顺时针或逆时针方向排序，以便下一步连接生成泰森多边形。设离散点为o。找出以o为顶点的一个三角形，设为A；取三角形A除o以外的另一顶点，设为a，则另一个顶点也可找出，即为f；则下一个三角形必然是以of为边的，即为三角形F；三角形F的另一顶点为e，则下一三角形是以oe为边的；如此重复进行，直到回到oa边。

4、计算每个三角形的外接圆圆心，并记录之。

5、根据每个离散点的相邻三角形，连接这些相邻三角形的外接圆圆心，即得到泰森多边形。对于三角网边缘的泰森多边形，可作垂直平分线与图廓相交，与图廓一起构成泰森多边形。

大自然中的 Voronoi Diagram

大自然中的 Voronoi Diagram 图样非常常见，举凡长颈鹿身上的斑纹、蜻蜓翅膀的翅脉、波罗蜜的壳都是范例。它的无所不在是有原因的，通常生物的细胞在生长时，会在有限的空间中，尽可能长满整个空间。以下图为例，每个黑点为细胞初始的位置，若它们以等速的方式长大，最终细胞的分布就会像 Voronoi Diagram 一样。

Voronoi Diagram 的应用

空间应用

下图为英国布里斯托尔的空气质量Voronoi图可视化，显示了不同区域的最近的传感器位置的NO2浓度值。

找出伦敦霍乱源头

1854年伦敦苏活区爆发严重的霍乱疫情，造成 10% 的人口死亡。在当时的医疗论述「瘴气理论」认为黑死病、霍乱等流行病的传染是经由「坏空气」传播，但是John Snow 医师提出霍乱是经由污水传播的，并以Voronoi Diagram 证明他的理论是正确的。

John Snow 首先将伦敦市内的给水点标示出来，并且以走到给水点的步行距离，绘制出 Voronoi Diagram。切分出来的每个区块，代表该区块的家户离区块内的水井距离最近，有高机率去该水井取水。接着再将罹患霍乱的病例标示在地图上，结果发现大部分的病例都落在宽街（Board Street ）的给水点上。这样研究引起当局的注意，最终也证实了污水是霍乱重要的传染途径之一。 John Snow 在公共卫生学上的重大贡献，也让他被誉为「流行病学之父」。

以红点标记出给水点的位置，改以欧式距离作为计算距离的方式，绘制出 Voronoi Diagram。从图的结果看来，除了正中间的 Board Street 的给水点需要调查以外，Carnaby Street 和 Rupert Street 的给水点应该也要被停用。

可视化

Voronoi图支持空间地图的可视化和图表的可视化，地图的可视化方式较为简单，将生成的Voronoi的空间数据坐标绘制成线对象或者面对象即可，下图为基于Mapbox GL绘制的北京海淀区停车场分布和Voronoi图：

甜点创作

Voronoi Diagram 繁复的几何图形也受到艺术家的青睐。乌克兰烘培师 Dinara Kasko 以 Voronoi Diagram 创作的蛋糕 The Bubbles with exotic fruit，提供视觉与味觉的双重盛宴。

Python 实现

官方文档

Python 管理 2D 点的对象 cv2.Subdiv2D()

  • 添加点到 对象中
1
subdiv.insert(p)
  • 获得 Voronoi 图
1
(facets, centers) = subdiv.getVoronoiFacetList([])
  • 获得三角形列表
1
triangleList = subdiv.getTriangleList()

示例代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
import cv2
import numpy as np
import random


# 检查一个点是否在矩形内
def rect_contains(rect, point) :
    if point[0] < rect[0] :
        return False
    elif point[1] < rect[1] :
        return False
    elif point[0] > rect[2] :
        return False
    elif point[1] > rect[3] :
        return False
    return True


# 绘制一个点
def draw_point(img, p, color ) :
    cv2.circle( img, p, 2, color, 2)


# 绘制 delaunay 三角剖分
def draw_delaunay(img, subdiv, delaunay_color ) :
    triangleList = subdiv.getTriangleList()
    size = img.shape
    r = (0, 0, size[1], size[0])
    for t in triangleList :
        pt1 = (int(t[0]), int(t[1]))
        pt2 = (int(t[2]), int(t[3]))
        pt3 = (int(t[4]), int(t[5]))
        if rect_contains(r, pt1) and rect_contains(r, pt2) and rect_contains(r, pt3) :
            cv2.line(img, pt1, pt2, delaunay_color, 1)
            cv2.line(img, pt2, pt3, delaunay_color, 1)
            cv2.line(img, pt3, pt1, delaunay_color, 1)


# 绘制 voronoi 图
def draw_voronoi(img, subdiv) :
    ( facets, centers) = subdiv.getVoronoiFacetList([])
    for i in range(0,len(facets)) :
        ifacet_arr = facets[i]
        center = centers[i].astype('int32')
        ifacet = np.array(ifacet_arr)
        color = (random.randint(0, 255), random.randint(0, 255), random.randint(0, 255))
        cv2.fillConvexPoly(img, ifacet.astype('int32'), color)
        ifacets = np.array([ifacet])
        cv2.polylines(img, ifacets.astype('int32'), True, (0, 0, 0), 1)
        cv2.circle(img, (center[0], center[1]), 3, (0, 0, 0), 1)


if __name__ == '__main__':
    win_delaunay = "Delaunay Triangulation"
    win_voronoi = "Voronoi Diagram"
    # 当绘制三角形剖分时打开动画画板
    animate = True
    # 定义绘制颜色
    delaunay_color = (255,255,255)
    points_color = (0, 0, 255)

    img = np.zeros([500,500,3],dtype=np.uint8)

    img_orig = img.copy()
    # 创建用于Subdiv2D 的矩形
    size = img.shape
    rect = (0, 0, size[1], size[0])
    # 创建Subdiv2D 实例
    subdiv = cv2.Subdiv2D(rect)
    points = []

    points.append((100, 100))
    points.append((100, 200))
    points.append((200, 100))
    points.append((200, 200))
    points.append((200, 300))
    points.append((400, 400))
    points.append((300, 400))

    # 将点依次插入subdiv中
    for p in points :
        subdiv.insert(p)
        # 展示动画画板
        if animate :
            img_copy = img_orig.copy()
            draw_delaunay(img_copy, subdiv, (255, 255, 255))
            cv2.imshow(win_delaunay, img_copy)
            cv2.waitKey(400)

    # 绘制delaunay 三角剖分
    draw_delaunay( img, subdiv, (255, 255, 255) )
    for p in points :
        draw_point(img, p, (0,0,255))
    # 为Voronoi 图分配空间
    img_voronoi = np.zeros(img.shape, dtype = img.dtype)
    # 绘制 Voronoi 图
    draw_voronoi(img_voronoi,subdiv)
    cv2.imshow(win_delaunay,img)
    cv2.imshow(win_voronoi,img_voronoi)
    cv2.waitKey(0)
  • 展示效果：

参考资料



文章链接：
https://www.zywvvd.com/notes/study/image-processing/voronoi/voronoi/

“觉得不错的话，给点打赏吧 ୧(๑•̀⌄•́๑)૭”

微信二维码

微信支付

支付宝二维码

支付宝支付

Image_Processing
#Image_Processing
Voronoi 图
https://www.zywvvd.com/notes/study/image-processing/voronoi/voronoi/
作者
Yiwei Zhang
发布于
2024年7月4日
许可协议